1. а)  .
.
б) 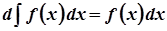 .
.
в) 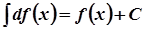 .
.
2. а) 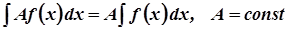 .
.
б)  .
.
в)  , якщо
, якщо 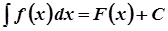 .
.
Заміна змінної

 →
→ 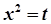
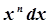 →
→ 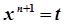
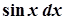 →
→ 
 →
→ 
 →
→ 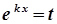
 →
→ 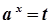
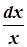 →
→  ,
, 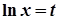
 →
→ 
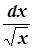 →
→ 
 →
→  ,
, 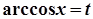
 →
→  ,
, 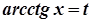
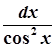 →
→ 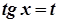
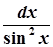 →
→ 
Інтегрування частинами
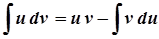
1)  ;
; 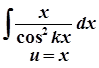 ;
; 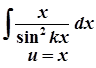 .
.
2)  ,
,  ;
; 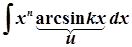 ;
; 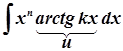 .
.
3) Циклічні інтеграли
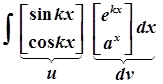 ;
;  ;
; 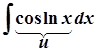 ;
;  .
.
Таблиця інтегралів
1. 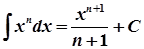 ,
, 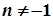

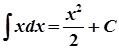

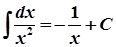
2. 
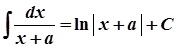
3. 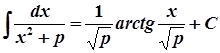

4. 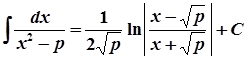
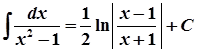
5. 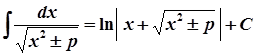
6. 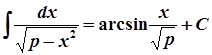
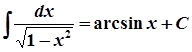
7. 
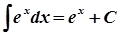
8. 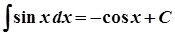
9. 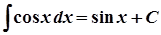
10. 
11. 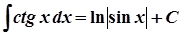
12. 
13. 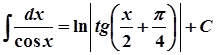
14. 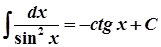
15. 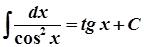
16. 

17. 
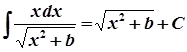

КОМПЛЕКСНІ ЧИСЛА
Вираз вигляду 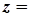
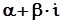 , де
, де 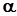 і
і 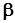 - дійсні числа,
- дійсні числа, 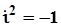 , називається комплексним числом (в алгебраїчній формі).
, називається комплексним числом (в алгебраїчній формі).
Комплексне число 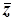 =
=  називається комплексно-спряженим числом до комплексного числа
називається комплексно-спряженим числом до комплексного числа 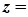
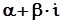 .
.
Дії над комплексними числами. Нехай дано два комплексні числа: 
 та
та 
 . Тоді
. Тоді
1) 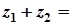
 ;
;
2) 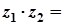
 ;
;
3) 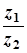 =
= 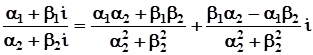 .
.
Для будь-якого комплексного числа 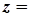
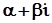 маємо:
маємо: 
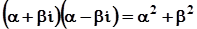 .
.
Величина 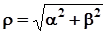 називається модулем комплексного числа. Кут
називається модулем комплексного числа. Кут 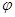 , що визначений наступними рівностями
, що визначений наступними рівностями
 ,
,  , називається аргументом комплексного числа.
, називається аргументом комплексного числа.
Будь-яке комплексне число можна записати в тригонометричній формі:
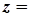
 ,
,
де  .
.
Приклад. Дано комплексне число  . Треба:
. Треба:
записати дане число в алгебраїчній та в тригонометричній формах.
Розв’язання Приведемо комплексне число 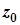 до алгебраїчної форми:
до алгебраїчної форми: 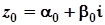 .
.
Для цього помножимо чисельник та знаменник дроби 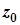 на число
на число  , комплексно-спряжене до знаменника. Отримаємо:
, комплексно-спряжене до знаменника. Отримаємо:
.
Це й є алгебраїчна формакомплексногочисла 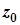 , де
, де 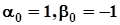 .
.
Приведемо комплексне число 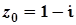 до тригонометричного виду:
до тригонометричного виду:  , де
, де  - модуль комплексного числа
- модуль комплексного числа 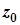 ,
, 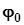 - аргумент цього числа.
- аргумент цього числа.
Знайдемо  . Для знаходження
. Для знаходження 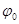 маємо систему:
маємо систему:
 ,
,
або 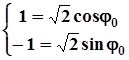 ,
,
і тоді  . Звідси, тригонометрична форма комплексного числа
. Звідси, тригонометрична форма комплексного числа 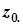 має вигляд:
має вигляд: 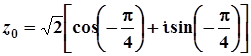 .
.

КОНТРОЛЬНА РОБОТА №1
Тема Матриці. Визначники. Системи лінійних алгебраїчних рівнянь. Елементи векторної алгебри. Аналітична геометрія на площині. Аналітична геометрія у просторі. Функції. Обчислення границь. Диференційованість функцій. Невизначений інтеграл. Комплексні числа
Завдання до контрольної роботи № 1
1. Завдання. Розв’язати систему рівнянь методом Крамера.
1.  6.
6. 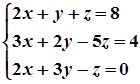
2. 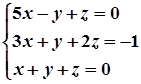 7.
7. 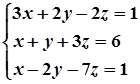
3. 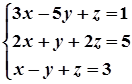 8.
8. 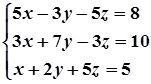
4. 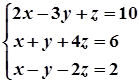 9.
9. 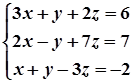
5. 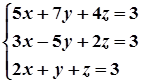 10.
10. 
2. Задача. Задано координати вершини піраміди. Знайти її об’єм.
1..
2..
3..
4..
5..
6..
7..
8..
9..
10..
3. Задача. Задано координати вершин трикутника АВС.
Знайти:
1. Рівняння медіани ВК.
2. Довжину медіани ВК.
3. Рівняння прямої, що проходить через вершину А паралельно стороні ВС.
4. Рівняння висоти АР.
5. Довжину висоти АР.
6. Точку перетину медіани ВК та висоти АР.
7. Кут КВС.
8. Площу трикутника АВС.
| Варіант | 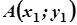
| 
| 
|
| (-4; 2) | (1; 5) | (-1; 5) | |
| (4; 1) | (2; 3) | (1; -2) | |
| (-6; 1) | (3; 7) | (-2; 5) | |
| (-1; 6) | (3; 3) | (8; 0) | |
| (1; -1) | (2; 5) | (4; -1) | |
| (4; -3) | (-1; 5) | (5; -1) | |
| (3; 0) | (1; 6) | (7; -2) | |
| (0; 2) | (-1; 6) | (-4; -2) | |
| (2; 1) | (3; -1) | (9; -1) | |
| (-1; 2) | (1; 8) | (4; 4) |
4. Задача. Побудувати лінію. Знайти довжини осей, координати фокусів, ексцентриситет, рівняння директрис (для еліпса), рівняння асимптот (для гіперболи).
| Варіант | Рівняння лінії | Варіант | Рівняння лінії |

| 
| ||

| 
| ||

| 
| ||

| 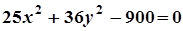
| ||
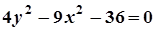
| 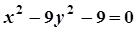
|
5. Задача. Знайти координати центра і радіус кола. Побудувати коло.
| Варіант | Рівняння кола | Варіант | Рівняння кола |
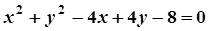
| 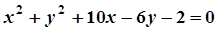
| ||

| 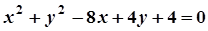
| ||
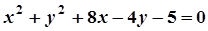
| 
| ||

| 
| ||
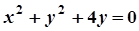
| 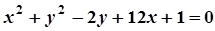
|
6.Завдання. Знайти границі функцій, не користуючись правилами Лопіталя.
1. а) 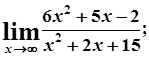 б)
б) 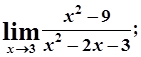
в) 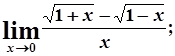 г)
г) 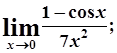
д) 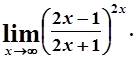
2. а) 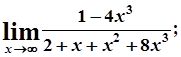 б)
б) 
в) 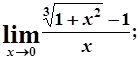 г)
г) 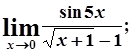 д)
д)  ;
;
3. а)  б)
б) 
в) 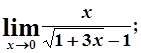 г)
г) 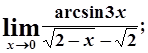
д) 
4. а)  б)
б) 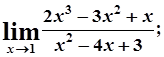
в) 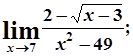 г)
г) 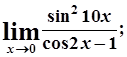
д) 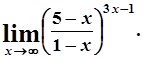
5. а)  б)
б) 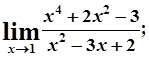
в)  г)
г) 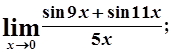
д) 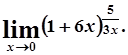
6. а) 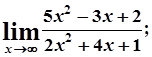 б)
б) 
в) 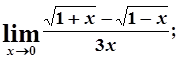 г)
г)  д)
д) 
7. а)  б)
б) 
в)  г)
г) 
д) 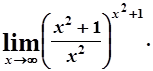
8. а)  б)
б) 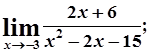
в) 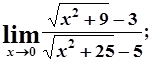 г)
г) 
д) 
9. а) 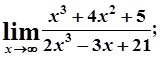 б)
б) 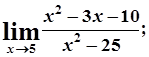
в) 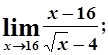 г)
г) 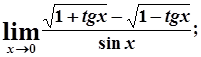
д) 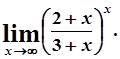
10. а) 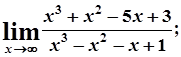 б)
б) 
в) 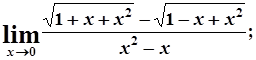 г)
г) 
д) 
7. Завдання. Знайти похідні 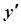 даних функцій.
даних функцій.

| 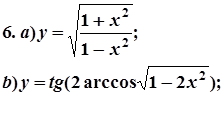
|
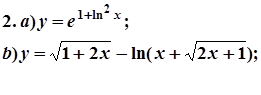
| 
|
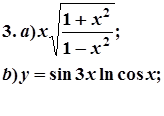
| 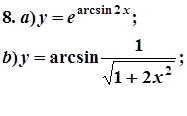
|
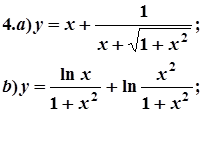
| 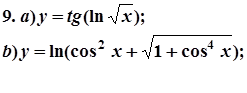
|
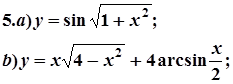
| 
|
8. Завдання. Записати рівняння дотичної та нормалі до лінії, що задана рівнянням y = f(x) в точці х0.
1. 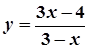 ,
, 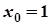 ; 6.
; 6. 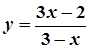 ,
, 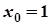 ;
;
2. 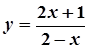 ,
, 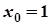 ; 7.
; 7. 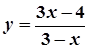 ,
,  ;
;
3. 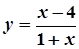 ,
, 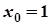 ; 8.
; 8. 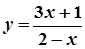 ,
,  ;
;
4.  ,
, 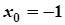 ; 9.
; 9.  ,
,  ;
;
5.,; 10.,.
9. Завдання. Знайти екстремуми функції:
1.  ; 6.
; 6. 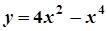 ;
;
2.  ; 7.
; 7. 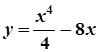 ;
;
3. 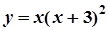 ; 8.
; 8.  ;
;
4.  ; 9.
; 9.  ;
;
5.; 10..
10. Завдання. Знайти невизначені інтеграли:
1. а) 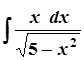 ; 6. а)
; 6. а) 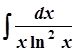 ;
;
б) 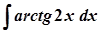 ; б)
; б) 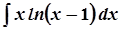 ;
;
в) 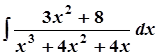 ; в)
; в)  ;
;
2. а) 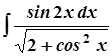 ; 7. а)
; 7. а) 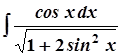 ;
;
б) 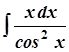 ; б)
; б)  ;
;
в) 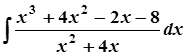 ; в)
; в) 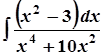 ;
;
3. а)  ; 8. а)
; 8. а) 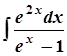 ;
;
б) 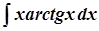 ; б)
; б) 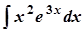 ;
;
в)  ; в)
; в) 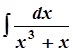 ;
;
4. а)  ; 9. а)
; 9. а) 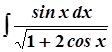 ;
;
б) 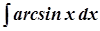 ; б)
; б) 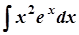 ;
;
в) 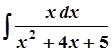 ; в)
; в) 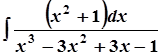 ;
;
5. а) 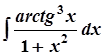 ; 10. а)
; 10. а)  ;
;
б) 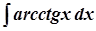 ; б)
; б) 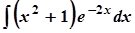 ;
;
в) 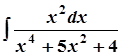 ; в)
; в)  ;
;
11. Завдання. Представити комплексне число в алгебраїчній та тригонометричній формі:
1. 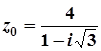 ; 6.
; 6. 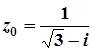 ;
;
2. 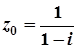 ; 7.
; 7. 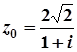 ;
;
3. 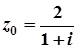 ; 8.
; 8.  ;
;
4.  ; 9.
; 9. 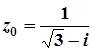 ;
;
5.; 10..
2. ПРОГРАМА ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА”
(2 семестр)






