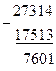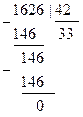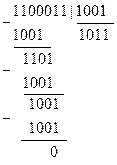При решении числовых задач используются технические средства, объектом преобразования которых является числа. В современных ЭВМ любая информация представляется в виде двоичных кодов, т.е. последовательности цифр 0 и 1. В связи с этим при работе с ЭВМ часто приходится использовать системы счисления, иные от привычной десятичной системы счисления.
Счислением называется порядок построения и записи знаков для изображения количественных характеристик числовой информации. Определенный способ обозначения и написания числовой информации называют системой счисления. В качестве знаков для изображения чисел в настоящее время пользуются преимущественно цифрами, Таким образом, системой счисления называется совокупность приемов записи и наименования действительных чисел посредством цифровых знаков - цифр. Системы счисления играют важную роль при конструировании вычислительной машины. Принцип работы машины зависит во многом от выбора способа изображения чисел.
Система счисления по признаку изменений значений знаков в зависимости от их положения в числе делятся на позиционные и непозиционные.
Непозиционные системы счисления - это системы, у которых количественное значение цифры зависит не от ее положения в ряду чисел, а только от ее написания. Из-за сложности и громоздкости этих систем они не применяются при обработки информации. Например, цифры римской системы счисления. Число III-3, значение каждой I одно и то же независимо от ее позиции в числе.
Позиционная система счисления называется потому, что значение каждой цифры зависит не только от ее написания, но и от места (позиции), которое занимает цифра в записанном числе, Число 929, знаки 9 имеют разное значение. Знак который находится справа характеризует девять единиц, а тот же знак слева показывает девять сотен. Позиционная система счисления строится по определенному основанию и характеризуется использованием фиксированного количества знаков, которое зависит от основания систем.
Основанием (модулем) системы называется число цифр (число единиц) одного разряда. Например, основание десятичной системы- 10, т.к. число цифр в одном разряде этой системы равно 10 (0 до 9) (количество цифр, применяемых для записи чисел в данной системе). Основание показывает во сколько раз изменяется значение цифры при ее переходе в следующий соседний разряд. Основание десятичной системы счисления показывает, что переход цифры в соседний разряд вызывает изменение ее значения в 10 раз. Числа, соответствующие полному набору знаков систем счисления, называются базой системы. Например, база в десятичной системе счисления состоит из десяти последовательных чисел от 0 до 9 (изображение арабскими цифрами).
Запись числа ведется последовательно по позициям (разрядам).
аn,..... a1, a0, a-1,..... а-n
Слева от запятой позиции нумеруется в порядке возрастания (положительные) чисел, справа от запятой в порядке возрастания (отрицательные) чисел Значение цифры в нулевой позиции равно значению числа базы; значение цифры в позиции «один» — в 10 раз больше его, а в позиции «минус один» - в 10 раз меньше. Следовательно, можно записать
an Sn+...+ a1 S1+a0S0 +a1S-1+....+anS-n
Например, 929
9·102 +2·101 +9·100=900+20+9
0,52
0,52=5·10-1 + 2·10-2
В ЭВМ наиболее пригодна система счисления, требующая фиксации только двух цифр в разряде: 0 и 1. При ее применении достигается простота конструкции и компактность арифметического устройства, а также эффективность выполнения вычислений. Двоичная система позволяет применять аппарат математической логики. К недостаткам двоичной системы счисления можно отнести; значительное увеличение, примерно в 3,3 раз, разрядности для изображения чиста, необходимость перевода для обработки чисел из десятичной в двоичную систему, а после обработки - из двоичной в десятичную. Т.к. ЭВМ обрабатывают и хранят данные только в виде набора единиц и нулей (два устойчивых состояния), то команды также представляются в машине в двоичной системе. А поскольку команд в ЭВМ насчитывается от нескольких десятков до 200 с лишним, то машина имеет дело с 6 - 8 разрядными двоичными числами для обозначения кодов операций и значительно большими — для обозначения адресов. Программисту трудно закончить команды (даже коды операции) с таким числом знаков. Поэтому используют систему счисления, которая с одной стороны относительно малозначная и с другой — кратка основанию двоичной системы (представляет степень двойки), т.е. числа легко переводятся. Это восьмеричная и шестнадцатеричная системы счисления.
Шестнадцатеричная система употребляется какпромежуточная при общении с машиной именно для записи чисел. Имеется 16 цифр:
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F (A-10, B-11, C-12, D-13, E-14, F-15).
В восьмеричной системе счисления - число 8 является в виде 10
127=1·102+7·101+7·100 десятичная система счисления
127=1·82+7·81+7·80 восьмеричная система счисления.
В двоичной системе счисления основанием является число 2, которое записывается цифрами 10
1·24+1·23+0·22+0·21+1·20=25
Запись двоичной системы счисления
аn·2n+...+a1·21+a0·20+a1·2-1+...+an·2-n
Кроме того, в ЭВМ применяется двоично-десятичная система счисления. Эта система представляет собой соединение, как двоичной, так и десятичной системы счисления. Каждый разряд десятичного числа представляется в двоичной системе счисления, а запись всего числа производится в десятичной системе, т.е. в виде разрядов единиц десятков, сотен и т.д.
Например, число 769, можно представить в двоично-десятичной системе счисления следующим обрезом
769(10)=011101101001(2-10)
Правила перевода чисел из одной системы счисления в другую.
Чтобы перевести целое число из одной десятичной системы счисления в другую позиционную систему, необходимо число одной системы счисления последовательно делить на основание той системы, в которую переводится данное число. При этом деление производится до тех пор, пока частное не окажется меньше основания получаемой системы счисления. Число в новой системе счисления формируется из остатков от деления, начиная с последнего. Иначе говоря, последнее частное становится высшим разрядом числа
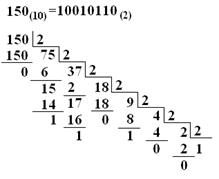

Чтобы перевести правильную дробь из системы счисления с большим основанием, необходимо последовательно умножать дробную часть на основание другой системы счисления. Цифры, стоящие слева от занятой, образуют переведенное число, причем запись их производится сверху вниз. В частном случае последовательное умножение прекращается, когда очередная дробь равна нулю; обычно заранее задается число разрядов после занятой в переведенном числе.
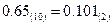
| 
| 
| 
|
Для перевода смешанного числа из одной системы счисления в другую необходимо перевести его целую и дробные части, затем объединить полученные результаты в одно смешанное число в новой системе счисления.
18,65(10)=10010,101(2)
Спрактической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатеричных чисел. Для этого воспользуемся табл. 4.1 чисел от 0 до 15 (в десятичной системе счисления), представленных в других системах счисления.
Таблица 4.1
Соответствие чисел в различных системах счисления
| Десятичная | Шестнадцатеричная | Восьмеричная | Двоичная |
| А | |||
| В | |||
| С | |||
| D | |||
| Е | |||
| F |
Для перевода чисел из двоичной системы счисления в восьмеричную необходимо в двоичном числе направо и налево от занятой выделить триады, после чего каждая триада представляется восьмеричной цифрой

Для перевода чисел из восьмеричной системы счисления в двоичную необходимо каждую цифру восьмеричного числа представить тремя двоичными цифрами (триадами).
| Восьмеричные числа | 4 | |||||||
| Триады |
Сущность перевода из системы счисления с меньшим основанием. Чтобы перевести целое число из системы счисления с меньшим основанием, нужно представить его каксумму произведений цифр числа на основание системы в соответствующей степени и произвести вычисления по правилам системы счисления переведенного числа
376(8)=3·82+7·81+6·80=192+56+6=254(10)
11111110(2)=l·27+1·26+1·25+1·24+1·23+1·22+1·21+0·20=254(10)
1011011101(2)=1335(8)
0,24(8)=2·8-1+4·8-2=2/8+4/64+20/64=0,3125(10)
0,0101(2)=0·2-1+1·2-2+0·2-3+1·2-4=0,3125(10)
0,01101011011(2)=0,3266(8)
Для перевода чисел из десятичной системы счисления в двоично-десятичную необходимо каждую цифру десятичного числа выразить в виде соответствующей тетрады.
| Десятичные-числа | ||||||||||
| Двоично-десятичные |
934,5(10)=100100110100,0101(2-10)

9834(10)=1001100000110100(2-10)
0,3769(10)=0,00110111101101001(2-10)
10011101100111(2-10)=2767(10)
0,001110011000100(2-10) =0,3984(10)
Для перевода чисел из шестнадцатеричной системы счисления в двоичную следует каждую цифру шестнадцатеричного числа представить четырьмя двоичными цифрами (тетрадой).
| шестнадцатеричные числа | 3 | А | B | C | D | Е | F | |||||||||
| Тетрады |
Арифметические операции
Двоичные таблицы сложения вычитания, умножения и деления;
| 0+0=0 | 0-0=0 | 0·0=0 | 1/1=1 |
| 0+1=1 | 1-0=1 | 1·0=0 | 0/1=0 |
| 1+0=1 | 1-1=0 | 0·1=0 | 1 / 0 — нельзя |
| 1+1=10 | 10-1=1 | 1·1=1 |
Восьмеричная система счисления
Таблица умножения
| X | |||||||
| 7 | 34 |
Таблица сложения
Примеры арифметических операций в двойной и восьмеричной системах счисления.