Аксиомы (постулаты) алгебры логики

1. Дизъюнкция двух переменных равна 1, если хотя бы одна из них равна 1 и равна 0, если обе переменные равны 0:

0+0=0;

0+1=1;

1+0=1;

1+1=1.

2. Конъюнкция двух переменных равна 0, если хотя бы одна пе­ременная равна 0 и равна 1, если обе переменные равны 1:

0∙0=0;

0∙1=0;

1∙0=0;

1∙1=1.

3.Инверсия одного значения переменной совпадает с ее другим значением:

1= 0;

0 = 1.

Элементарные булевые функции

Булевой функцией f(x₁, x₂,..., x_n) называется функция, которая принимает два значения 0 или 1 в зависимости от переменных х₁, каждая из которых может также принимать только два значения 0 или 1.

Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов.

Любая булевая функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных, а в правой части - значения функции. Пример такого задания для трех переменных представлен в таблице.

Представление булевой функции

x1	x2	x3	f(х1,х2,х3)

Для формирования столбца значений переменных удобен лексико­графический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100=011+1.

Булевая функция п переменных может иметь 2ⁿ наборов. Поскольку функция принимает только два значения, общее число булевых функций и переменных равно 2²ⁿ. Таким образом, функция одной переменной может иметь четыре значения: у = х; у = -x (отрицание х); у = 0 (константа 0); у = 1 (константа 1).

Из них выделим функцию "отрицание x" (обозначается -x ). Эта функция представлена в таблице

Функция отрицания

x	-x

Булевых функций двух переменных - 16. Те из них, которые имеют специальные названия, представлены в таблице.

Булевы функции двух переменных

x 1 x 2	x 1 Ú x 2	x 1 & x 2	x 1 É x 2	x 1 ~ x 2	x 1 Å x 2	x 1 ¯ x 2	x 1 ½ x 2
0 0
0 1
1 0
1 1

В таблице представлены следующие функции двух переменных:

x ₁ Ú x ₂– дизъюнкция;

x ₁ & x ₂– конъюнкция;

x ₁ É x ₂– импликация;

x ₁ ~ x ₂– эквивалентность;

x ₁ Å x ₂– сложение по модулю 2;

x ₁ ¯ x ₂– стрелка Пирса;

x ₁ ½ x ₂ – штрих Шеффера

Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.

Формулы логики булевых функций

Формула логики булевых функций определяется индуктивно следующим образом:

1. Любая переменная, а также константы 0 и 1 есть формула.

2. Если A и B - формулы, то A, A Ú B, A & B, A É B, A ~ B есть формулы.

3. Ничто, кроме указанного в пунктах 1-2, не есть формула.

Пример 2.1.

Выражение (- x Ú y)&((y É z)~ x) является формулой

Выражение (– x&y É z ~ x) не является формулой

Часть формулы, которая сама является формулой, называется подформулой.

Пример 2.2.

x& (y É z) – формула; y É z – ее подформула.

Функция f есть суперпозиция функций f₁,f₂,...,f_n, если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.

Пример 2.3.

f₁ = х₁&х₂ (конъюнкция); f₂ =-x (отрицание).

Возможны две суперпозиции:

1)f=f₁(f₂) = (—х₁)&(—х₂) - конъюнкция отрицаний;

2)f=f₂(f₁) = -(x₁&х₂) - отрицание конъюнкции.

Порядок подстановки задается формулой.

Всякая формула задает способ вычисления функции, если известны значения переменных.

Пример 2.4.

Построим таблицу значений функции

f (x₁,х₂,х₃)=(х₂ É х₃)~(x₁ Ú х₂).

Вычисление функции f(x₁ х₂, х₃)

x 1	x 2	x 3	x 3	x 2É x 3	(x 2É x 3)	x 1	x 1 Ú x 2	f (x1,х2,х3)

Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций:, &, Ú, É и ~.

Графы и деревья

Такая структура, как граф (в качестве синонима используется также термин «сеть»), имеет самые различные применения в информатике и в смежных приклад­ных областях, поэтому познакомимся с основными понятиями теории графов.

Граф G = (V, Е) задается парой конечных множеств V и Е. Элементы первого множества v1, v2,..., vM называются вершинами графа (при графическом представ­лении им соответствуют точки). Элементы второго множества e1, e2,..., eN называ­ют ребрами. Каждое ребро определяется парой вершин (при графическом представ­лении ребро соединяет две вершины графа). Если ребра графа определяются упоря­доченными парами вершин, то такой граф называют ориентированным – орграфом (на чертеже при изображении ориентированного графа на каждом ребре ставят стрелку, указы­вающую его направление). Ориентированный граф с пятью вершинами и семью ребрами изображен на рис. 3.2.

Рис. 3.2. Пример ориентированного графа

 

Если порядок ребер не имеет значения, то граф называется неориентированным.

Если две вершины соединены двумя или более ребрами, то эти ребра называют параллельными (например, ребра е 4 и е5). Если начало и конец ребра совпадают, то такое ребро называется петлей (например, ребро e7).

Граф без петель и параллель­ных ребер называется простым.

Если ребро е_к определяется вершинами v_i и v_j (будем обозначать этот факт следующим образом: е_k = (v_i, v_j), то говорят, что ребро е_к инцидентно вершинам v_i и v_j.

Граф G(E,U) называется конечным, если множество Е вершин конечно. Граф G(E,U), у которого любые две вершины соединены ребром, называется полным. Если хотя бы две вершины соединены несколь­кими ребрами, то такой граф называется мультиграфом. Две верши­ны е_i, е_j ÎЕ называются смежными, если они соединены ребром. Чис­ло ребер, инцидентных данной вершине е_i, называется локальной степенью этой вершины р(е_i). Число ребер r графа G(E,U) определя­ется выражением

где n — количество вершин в графе.

Рассмотрим граф, изображенный на рис. 3.3.

Рис. 3.3. Ориентированный граф

 

Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество ребер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), (5, 3)}. Ребро (5, 3) — является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных сте­пеней для каждой вершины:

р(1) = 3; р(2) = 2; р(3) = 3; р(4) = 2; р(5) = 2; р = (3+2+3+2+2)/2=6.

Важным в теории графов является понятие части графа G(E,U), который обозначается G'(E',U') Í G(E,U).

Множества вершин и ребер части графа являются подмножества­ми вершин и ребер исходного графа Е'ÍЕ, U' ÍU. Многие задачи на графах состоят в определении частей графа с заданными свойствами. Часть графа G'(E',U')ÍG(E,U) называется подграфом графа G(E,U), если Е'ÍЕ, а подмножество U'ÍU образовано только реб­рами, инцидентными вершинам множества Е'.

Полным графом называется граф G(E,U), у которого каждая вер­шина соединена ребрами с остальными вершинами (рис. 3.4).

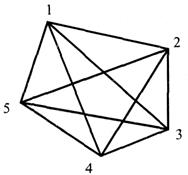
Рис. 3.4. Полный граф

Обязанность графов

Маршрутом графа G называется последовательность ребер S=(u₁,u₂,... u_n), в которой каждые два соседних ребра имеют общую вершину, т.е. u₁= (e₁, e₂); u₂= (e₂, е₃);... u_n= (e_n, е_n+1). Не исключено, что одно и то же ребро может встречаться несколько раз на одном маршруте.

Две вершины е_i и е_j называются связанными, если существует мар­шрут из е_i в е_j.

Компонентой связности графа называется подмножество его вер­шин с инцидентными им ребрами, такое, что любая вершина свя­зана с любой другой вершиной маршрута. Например, из графа на рис. 3.5 можно выделить следующие две компоненты связанности, показанные сплошной линией.

Рис. 3.5. Компоненты связанности графа

Простой цепью, или простым путем, называется маршрут, в ко­тором ни одно ребро не повторяется дважды. Элементарной цепью или элементарным путем называется маршрут, в котором ни одна верши­на не повторяется дважды. Циклом в графе называется маршрут, у которого начальная вершина совпадает с конечной. Например, следу­ющий граф имеет цикл S = (1, 2, 3, 5, 4, 1) (рис. 3.6).

Рис. 3.6. Цикл в графе

Цикл, проходящий по всем ребрам графа только один раз, называется эйлеровым циклом. В теории графов доказывается теорема, определяющая, содержит ли граф эйлеров цикл. Оказывается, конечный граф содержит эйлеров цикл тогда и только тогда, когда он свя­зан, и все его локальные степени вершин четные. Важной приклад­ной задачей теории графов является задача поиска в графе цикла, проходящего через каждую вершину только один раз. Такие циклы называются гамильтоновыми циклами.

Задание графа

Граф может задаваться в виде рисунка, аналитически, в виде матрицы. Выше приводилось задание графа в виде рисунка. Анали­тическое задание состоит в задании элементов множества вершин Е={е₁, е₂,... е_n} и множества ребер U = {u₁, u₂,... u_m}.

Для выполнения различного рода формальных преобразований над графами удобно использовать их матричные задания. Матрица А размерностью n ´ n называется матрицей смежности графа G(E,U), если ее элементы образованы по правилу: элемент матрицы а_ij= m, если вершины е_i и е_j соединены m ребрами, и а_ij=0, если эти вершины не связаны ребрами. Матрица смежности имеет число строк и столбцов, равное количеству вершин графа.

Матрица А размерностью n ´ m называется матрицей инцидент­ности графа G(E,U), если ее элементы образованы по правилу: элемент матрицы b_ij=1, если вершина е_i инцидентна ребру u_j и b_ij=0 в про­тивном случае. Так как каждое ребро инцидентно двум вершинам, то в каждой строке этой матрицы ровно два ненулевых элемента.

Построим матрицы смежности и инцидентности для графа, изображенного на рис. 3.7.

Рис. 3.7. Пример графа.

 

Матрица смежности будет состоять из пяти строк и пяти столбцов.

Матрица инцидентности будет состоять из пяти строк и шести столбцов.

	а	b	с	d	е	f

Анализ приведенных здесь понятий и определений показывает, что в качестве моделей графы удобно использовать в тех случаях, когда рассматривается система каких-либо объектов, между которыми существуют определенные связи, отноше­ния, когда изучается структура системы, возможности ее функционирования. В информатике графы используются в разделах: операционные системы, алгорит­мизация, структуры данных, информационное моделирование и др.

Весьма важным является связанный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны един­ственным путем. Вершина называется концевой, если ей инцидентно не более одного ребра; одна из концевых вершин может быть выбрана в качестве корня.

Лес - это любой граф без циклов. На рис. 3.8 показаны возможные деревья с пятью вершинами.

Рис. 3.8. Примеры деревьев

Деревья бывают также ориентированные и неориентирование.

Нижеследующие определения неориентированного дерева, как легко показать, эквивалентны друг другу. Неориентированное дерево есть связный граф, содержащий п вершин и n-1 ребер, либо связный граф, не имеющий циклов, либо граф, в котором каждая пара вершин соединена одной и только одной простой цепью.

Если G = (X, А) - неориентированный граф с n вершинами, то остовным деревом (или, короче, остовом) графа G называется всякий остовный подграф графа G, являющийся деревом (в смысле приведенного выше определения). Например, если G - граф, показанный на рисунке (а), то граф на рисунке (б) является остовом графа G, как и граф, изображенный на рисунке (в). Из сформулированных выше определений вытекает, что остов графа G можно также рассматривать как минимальный связный остовный подграф графа G, где «минимальность» понимается в том смысле, что никакое собственное подмножество ребер этого остова не образует связный остовный подграф графа G.