Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа 
есть решение уравнения 
Десятичный логарифм числа существует, если 
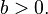Принято обозначать его 
.
Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log e (x) или иногда просто log(x), если основание e подразумевается.
Правила действий с логарифмами
Правила действий с логарифмами (a, b, c > 0)
1) логарифм произведения: 
2) логарифм частного: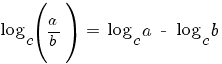 
3) логарифм степени: 
4) логарифм степенного основания: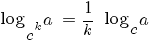 
5) логарифм корня: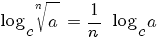 
6) переход к новому основанию: 
Дополнительные формулы:
Логарифмические и показательные уравнения и неравенства обычно решаются путем приведения всех выражений, содержащих логарифмические и показательные функции, к одному основанию и последующей замены неизвестной, сводящей задачу к решению алгебраического уравнения или неравенства.
При решении неравенств используют свойства:
1) 
2) 
Переход к новому основанию
Можно выбрать одно удобное основание, например а, и привести любую степень к основанию а, то есть представить любую степень 
в виде 
при некотором k. Этот коэффициент k и есть логарифм: 
поэтому, обозначая 
через k, мы получим:
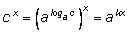
При логарифмировании можно также выбрать одно удобное основание и сводить все логарифмы к этому основанию. Для этого существует специальная формула, которую мы сейчас выведем.
Пусть мы хотим перейти от логарифмов по основанию а к логарифмам по другому основанию b. Запишем основное логарифмическое тождество: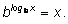 
Прологарифмируемего по основанию а: 
Получаем:
Преобразование алгебраических выражений
Действия с дробями:
| Сложение | Вычитание | Умножение | Деление |
| 
| 
| 
|
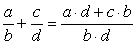
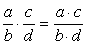
Перестановка членов пропорции:
| 
| 
| 
|
Производные пропорции
Дана пропорция 
, справедливы следующие пропорции:
| 
|
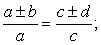
Формулы сокращенного умножения:
| 
|
| 
|
|
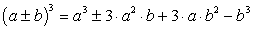
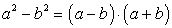
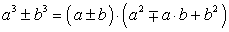
Преобразование рациональных выражений?
a 2−b 2 = (a−b)(a+b);
a−b) 2 = a 2−2ab+b 2;
(a+b) 2 = a 2+2ab+b 2;
a 3−b 3 = (a−b)(a 2+ab+b 2);
a 3+b 3 = (a+b)(a 2−ab+b 2);
(a+b) 3 = a 3+3a 2b+3ab 2+b 3;
(a−b) 3 = a 3−3a 2b+3ab 2−b 3.
Преобразования иррациональных выражений?
Преобразование степенных выражений?
Преобразование показательных?
Преобразование логарифмических выражений?
Предмет стереометрии
Стереометрия - (от др.-греч. στερεός, «стереос» — «твёрдый, пространственный» и μετρέω — «измеряю») — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.
Аксиомы стереометрии
