Целые и рациональные числа
Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью 
, числитель 
— целое число, а знаменатель 
— натуральное число, к примеру 2/3.
Целые числа — расширение множества натуральных чисел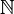 
, получаемое добавлением к 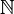нуля и отрицательных чисел вида 
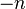. Множество целых чисел обозначается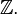 
Иррациональные числа
Иррациональное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби , где — целое число, — натуральное число. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Множество иррациональных чисел обычно обозначается заглавной латинской буквой 
в полужирном начертании без заливки. Таким образом: 
, т. е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
Действительные числа
Это вместе взятые множества рациональных и иррациональных чисел, т. е. любое положительное число, отрицательное число или нуль.
Подмножества множества действительных чисел
Объединение множества рациональных чисел и множества иррациональных чисел называется множеством действительных (или вещественных) чисел.
Множество действительных чисел обозначается символом R.
Очевидно,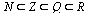 
.
Действительные числа изображаются на числовой оси Ох точками
Приближенное значение величины и погрешности приближений
В практических вычислениях и измерениях часто невозможно получить истинное значение величины. То значение, которое используется вместо истинного с той или иной степенью достоверности называется приближённым значением данной величины.
Примеры
- Продавец взвесил сыр на весах и получил 400 г. Величина 400 г. не является точной, но приближённой, так как весы имеют определённую погрешность измерения.
- При вычислении объёма заготовленной древесины сечения брёвен считают круглыми, а в качестве числа π берут приближённое значение 3,14.
Абсолютная погрешность
Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Относительная погрешность
Относительная погрешность – это число, отражающее степень точности измерения.
Это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Оценка погрешности результатов
