В предлагаемых методических указаниях решены задачи, аналогичные тем, которые даются студентам-заочникам в контрольных работах; обращено внимание на основные трудности и типичные ошибки, которые допускаются при выполнении контрольных работ.
Перед решением каждой задачи предлагаем ознакомиться с основными вопросами теории. Перечисленные ниже вопросы по каждой теме являются основными при защите контрольных работ.
КОНТРОЛЬНАЯ РАБОТА №2
Задачи 1-10
По теме «Введение в анализ» рассмотрите предварительно следующие вопросы о функциях и пределах:
1. Понятие функции, способы задания функции, область ее определения.
2. Основные элементарные функции, их свойства и графики.
3. Понятие предела функции в точке.
4. Понятие бесконечно малой функции 
и ее свойства: 
5. Понятие бесконечно большой функции : 
, ее свойства и связь с бесконечно малой функцией.
6. Теоремы о пределах: предел суммы, разности, произведения, частного функций.
7.Первый замечательный предел:
или 
8. Второй замечательный предел:
или в другой форме:
где e - иррациональное число: 
.
9. Эквивалентные бесконечно малые функции.
10. Виды неопределенностей и способы их раскрытия:
11. Понятие непрерывности функции в точке и на промежутке.
12. Теоремы о непрерывных функциях.
Задача. Найти пределы функций:
1. 
2. 
При 
3. 
4. 
Решение. Прежде всего заметим, что во всех примерах следует найти предел частного. Как известно, предел частного существует и равен частному пределов, если существуют пределы числителя и знаменателя и предел знаменателя не равен нулю.
1.а) 
Предел числителя и предел знаменателя дроби найдем, подставив в них предельное значение аргумента:
Здесь теорема о пределе частного применима.
б) 
При подстановке 
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида «ноль на ноль» 
Такая неопределенность раскрывается сокращением дроби на бесконечно малую функцию 
, в данном случае на 
, которая обращает числитель и знаменатель в нуль. Для этого нужно сначала разложить на множители числитель и знаменатель дроби.
Напомним формулу разложения квадратного трехчлена на множители: 
, где 
и 
-корни квадратного трех-
члена, которые находим из уравнения 
.
Разложим на множители числитель данной дроби:
; 
Следовательно: 
Разложим на множители знаменатель дроби:
;
Следовательно: 4х2+15х-4=4(х+4)(х-1 /4)=(х+4)(4х-1).
Тогда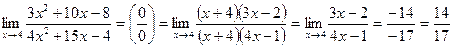 
в)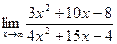 
При 
числитель и знаменатель дроби также стремятся к бесконечности. В этом случае теорема о пределе частного неприменима. Говорят, что имеется неопределенность вида «бесконечность на бесконечность» 
Чтобы ее раскрыть, каждый член числителя и знаменателя дроби разделим на 
в наивысшей для данного примера степени (то есть на 
), от чего величина дроби не изменится. Тогда получим:
так как 
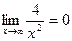
Замечание. Полезно заметить и запомнить, что предел отношения многочленов при равен отношению их коэффициентов при старших степенях.
2.
При подстановке предельного значения 
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Таким образом, перед нами вновь неопределенность вида
которая раскрывается сокращением дроби на бесконечно малую функцию 
. Для этого предварительно умножим числитель и знаменатель дроби на выражение, сопряженное иррациональному выражению в знаменателе, то есть на 
:
При умножении сопряженных выражений в знаменателе было использовано тождество 
З.Для решения примеров под номером 3 используется первый замечательный предел, с помощью которого раскрываются некоторые неопределенности вида
Примеры этого пункта можно решать также с помощью эквивалентных бесконечно малых функций. Две бесконечно малые функции 
и 
называются эквивалентными в точке 
, если предел их отношения в этой точке равен 1:
значит ~ при 
Например, при 
: 
~ 
; 
~ ;
~ ; 
~ .
При вычислении пределов бесконечно малые множители можно заменять на эквивалентные им.
4.Для раскрытия неопределенностей вида (
) применяется второй замечательный предел:
где e - иррациональное число, то есть бесконечная непериодическая десятичная дробь, ее приближенное значение: e ≈ 2,7
Найдем 
Очевидно, что 
Тогда
Задачи 11-20,21-30,31-40
Названные задачи относятся к теме «Дифференциальное исчисление и его приложения». Основные вопросы этой темы:
1. Понятие производной, ее геометрический и механический смысл.
2. Правила дифференцирования суммы, разности, произведения, частного и суперпозиции функций.
3. Формулы дифференцирования основных элементарных функций (таблица производных).
4. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.
5. Признаки возрастания и убывания для функции одной переменной.
6. Экстремумы функции одной переменной. Необходимое и достаточное условия существования экстремумов.
7.Вогнутость и выпуклость графика функции. Признаки выпуклости и вогнутости функции.
8.Точки перегиба. Необходимое и достаточное условия перегиба.
9.0бщая схема исследования функции. Построение графика функции.
Таблица производных
Пусть 
и 
две функции 
, 
, тогда
Заметим, что:
а) производная постоянной равна нулю:
б) постоянный множитель выносится за знак производной: 
в) 
