ряд А) расходится, ряд В) расходится
ряд А) сходится, ряд В) сходится
ряд А) сходится, ряд В) расходится
Решение:
Ряд  расходится, так как
расходится, так как 
Для исследования сходимости знакочередующегося ряда  применим признак сходимости Лейбница. Тогда
применим признак сходимости Лейбница. Тогда
1) вычислим предел 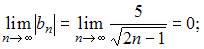
2) для любого натурального  справедливо
справедливо  то есть последовательность
то есть последовательность  монотонно убывает.
монотонно убывает.
Следовательно, ряд 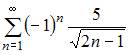 сходится.
сходится.
6. Сумма числового ряда 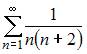 равна …
равна …
 - правильно
- правильно

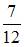

Решение:
Представим общий член этого ряда в виде суммы простейших дробей
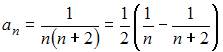 и вычислим n -ую частичную сумму ряда:
и вычислим n -ую частичную сумму ряда:
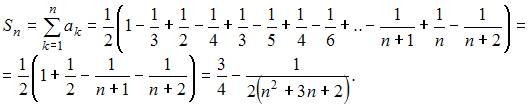
Тогда
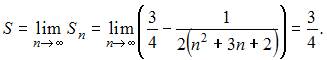
Тема 19: Область сходимости степенного ряда
1. Область сходимости степенного ряда  имеет вид …
имеет вид …
 - правильно
- правильно



Решение:
Вычислим предварительно радиус сходимости этого ряда по формуле  где
где 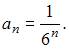 Тогда
Тогда 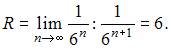 Следовательно, интервал сходимости ряда имеет вид
Следовательно, интервал сходимости ряда имеет вид  или
или 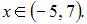
Для того чтобы найти область сходимости степенного ряда, исследуем сходимость ряда в граничных точках.
В точке  ряд примет вид
ряд примет вид  Данный ряд расходится, так как не выполняется необходимое условие сходимости числового ряда:
Данный ряд расходится, так как не выполняется необходимое условие сходимости числового ряда:

В точке  получаем знакочередующийся ряд
получаем знакочередующийся ряд  для которого
для которого  то есть ряд расходится.
то есть ряд расходится.
Таким образом, область сходимости ряда имеет вид 
2. Радиус сходимости степенного ряда  равен …
равен …
 - правильно
- правильно



Решение:
Радиус сходимости этого ряда можно найти по формуле  где
где 
Тогда

3. Радиус сходимости степенного ряда 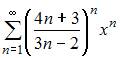 равен …
равен …
 - правильно
- правильно



Решение:
Радиус сходимости этого ряда можно найти по формуле  где
где  Тогда
Тогда 
4. Интервал сходимости степенного ряда  имеет вид …
имеет вид …
 - правильно
- правильно

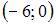

Решение:
Вычислим предварительно предел 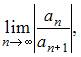 где
где 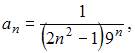 а именно
а именно 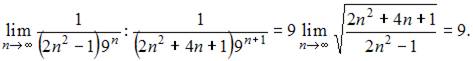
Тогда  и интервал сходимости ряда имеет вид
и интервал сходимости ряда имеет вид  или
или 
5. Для степенного ряда  вычислен предел
вычислен предел 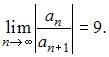 Тогда интервал сходимости данного ряда имеет вид …
Тогда интервал сходимости данного ряда имеет вид …
 - правильно
- правильно

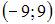

Решение:
Интервал сходимости данного ряда определяется как  где
где 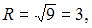
 Тогда интервал сходимости данного ряда определяется как
Тогда интервал сходимости данного ряда определяется как  или
или 
6. Интервал сходимости степенного ряда  имеет вид …
имеет вид …
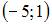 - правильно
- правильно


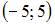
Решение:
Вычислим предварительно радиус сходимости этого ряда по формуле  где
где 
Тогда

Следовательно, интервал сходимости ряда имеет вид  или
или 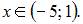
7. Радиус сходимости степенного ряда  равен …
равен …
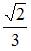 - правильно
- правильно



Тема 20: Ряд Тейлора (Маклорена)
1. Если 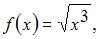 то коэффициент
то коэффициент  разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням  равен …
равен …
 - правильно
- правильно


Решение:
Так как коэффициенты данного ряда Тейлора вычисляются по формуле 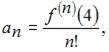 то вычислим последовательно производные:
то вычислим последовательно производные:
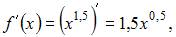

Тогда 
2. Разложение в ряд по степеням  функции
функции  имеет вид …
имеет вид …

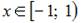 - правильно
- правильно


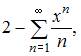

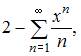

3. Если  то коэффициент
то коэффициент 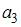 разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням  равен …
равен …
– 8
– 16
– 4
Решение:
Так как коэффициенты данного ряда Тейлора вычисляются по формуле  то вычислим последовательно производные:
то вычислим последовательно производные:
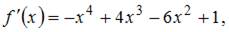

 .
.
Тогда 
4. Если  то коэффициент
то коэффициент  разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням  равен …
равен …

5. Ряд Маклорена для функции 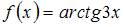 имеет вид …
имеет вид …

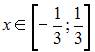 - правильно
- правильно


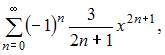
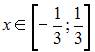
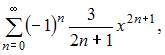

Решение:
Так как ряд Маклорена для функции 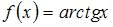 имеет вид
имеет вид

 то
то

при 
6. Если  то коэффициент
то коэффициент  разложения данной функции в ряд Маклорена равен …
разложения данной функции в ряд Маклорена равен …
– 10
– 6
Решение:
Так как разложение в ряд Маклорена функции 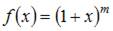 имеет вид
имеет вид
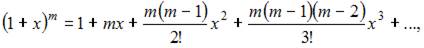 то
то  или, учитывая, что
или, учитывая, что  получаем
получаем 
7. Если  то коэффициент
то коэффициент  разложения данной функции в ряд Тейлора по степеням
разложения данной функции в ряд Тейлора по степеням 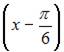 равен …
равен …
 - правильно
- правильно



Решение:
Так как коэффициенты данного ряда Тейлора вычисляются по формуле  то вычислим последовательно производные:
то вычислим последовательно производные:


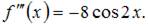
Тогда 
Тема 21: Типы дифференциальных уравнений
1. Уравнение  является …
является …
Уравнением Бернулли
линейным дифференциальным уравнением первого порядка
дифференциальным уравнением с разделяющимися переменными
однородным относительно 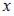 и
и  дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
Решение:
Уравнение  может быть сведено к уравнению вида
может быть сведено к уравнению вида 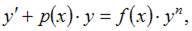 где
где  В данном случае
В данном случае 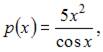

 Следовательно, данное уравнение является уравнением Бернулли.
Следовательно, данное уравнение является уравнением Бернулли.
2. Уравнение  является …
является …
Уравнением Бернулли
линейным дифференциальным уравнением первого порядка
дифференциальным уравнением с разделяющимися переменными
однородным относительно 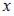 и
и  дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
3. Уравнение  является …
является …






