Разрыва второго рода
разрыва первого рода
непрерывности
устранимого разрыва
3. На отрезке 
непрерывна функция …
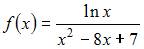- правильно
4. Количество точек разрыва функции 
равно …
Решение:
Точку 
называют точкой разрыва функции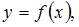 
если она не является непрерывной в этой точке. В частности, точками разрыва данной функции являются точки, в которых знаменатель равен нулю. Тогда
или 
Решив последнее уравнение, получаем три точки разрыва:
5. Точка 
является точкой разрыва функции …
- правильно
Тема 4: Асимптоты графика функции
1. Вертикальная асимптота графика функции 
задается уравнением вида …
- правильно
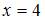
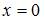
Решение:
Прямая является вертикальной асимптотой графика функции 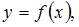если эта функция определена в некоторой окрестности точки и 
или 
Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной функции. Это точки, в которых 
или 
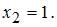Однако точка 
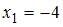не принадлежит области определения функции 
имеющей вид 
Вычислим односторонние пределы функции 
в точке 
и 
Следовательно, прямая будет вертикальной асимптотой.
2. Наклонная асимптота графика функции 
задается уравнением вида …
- правильно
Решение:
Прямая 
является наклонной асимптотой графика функции при 
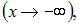если существуют конечные пределы:
или соответственно
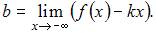
Вычислим эти пределы:
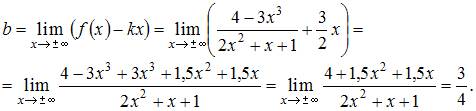
Следовательно, прямая является наклонной асимптотой графика данной функции как при 
так и при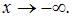 
3. Горизонтальная асимптота графика функции 
задается уравнением вида …
- правильно
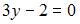
Решение:
Прямая 
является горизонтальной асимптотой графика функции при 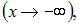если существует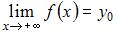 
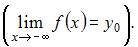
Вычислив предел
получаем уравнение горизонтальной асимптоты 
или 
4. Вертикальная асимптота графика функции 
задается уравнением вида …
- правильно
Решение:
Прямая является вертикальной асимптотой графика функции 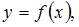если эта функция определена в некоторой окрестности точки и 
или 
Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной функции. Это точки, в которых знаменатель равен нулю, то есть 
или 
Вычислим односторонние пределы функции в точке
Аналогично и 
то есть прямая не является вертикальной асимптотой.
Вычислим односторонние пределы функции в точке 
Следовательно, прямая будет вертикальной асимптотой.
5. Горизонтальная асимптота графика функции 
задается уравнением вида …
- правильно
Решение:
Прямая является горизонтальной асимптотой графика функции при 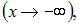если существует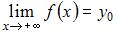
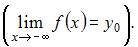
Вычислив предел
получаем уравнение горизонтальной асимптоты 
или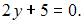 
6. Горизонтальная асимптота графика функции 
задается уравнением вида …
- правильно
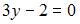
Решение:
Прямая является горизонтальной асимптотой графика функции при 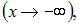если существует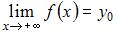
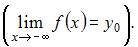
Вычислив предел
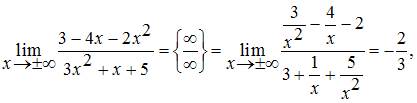
получаем уравнение горизонтальной асимптоты или
7. Наклонная асимптота графика функции 
задается уравнением вида …
- правильно
Тема 5: Производные первого порядка
1. Функция 
задана в параметрическом виде 
Тогда производная первого порядка функции по переменной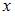 
имеет вид …
- правильно
Решение:
2. Производная функции 
равна …
- правильно
Решение:
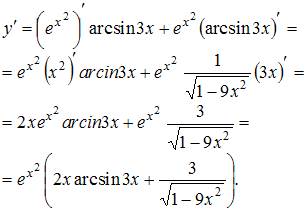
3. Производная функции 
равна …
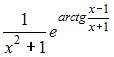- правильно
Решение:
4. Производная функции 
равна …
- правильно
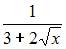
5. Функция задана в неявном виде 
Тогда производная первого порядка функции по переменной 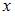имеет вид …
- правильно
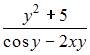
Решение:
Продифференцируем по 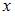обе части уравнения
Тогда
Решив последнее уравнение относительно 
получаем:
6. Производная функции 
равна …
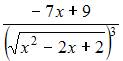- правильно
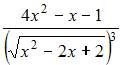
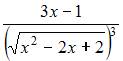
Решение:
Тема 6: Производные высших порядков
1. Производная второго порядка функции 
равна …
- правильно
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
2. Производная второго порядка функции 
равна …
- правильно
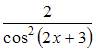
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
3. Производная второго порядка функции 
равна …
- правильно
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
4. Производная второго порядка функции 
равна …
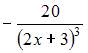- правильно
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
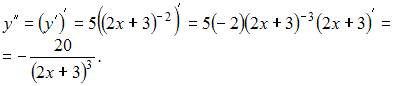
5. Производная второго порядка функции 
равна …
- правильно
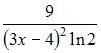
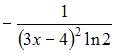
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
6. Производная второго порядка функции 
равна …
- правильно
Решение:
Вычислим производную первого порядка:
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть
Тема 7: Приложения дифференциального исчисления ФОП
1. Точка максимума функции 
равна …
– 3
– 1
Решение:
Определим критические точки функции, для чего вычислим производную первого порядка 
и решим уравнение 
а именно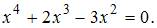 
Тогда 
Определим производную второго порядка 
и вычислим ее значения в критических точках:
Так как 
то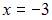 
будет точкой минимума.
2. График функции 
будет выпуклым вниз при …
- правильно
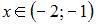
Решение:
График данной функции будет выпуклым вниз при условии, что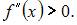 
Вычислим последовательно
и 
Тогда 
при 
3. Материальная точка движется прямолинейно по закону 
Тогда ускорение точки в момент времени 
равно …
– 5
4. Минимум функции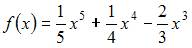 
равен …
- правильно
Решение:
Определим критические точки функции, для чего вычислим производную первого порядка 
и решим уравнение а именно 
Тогда 
Определим производную второго порядка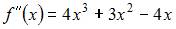 
и вычислим ее значения в критических точках:
Так как 
то 
будет точкой минимума. Следовательно, 
