- правильно
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
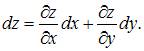
Тогда
5. Полный дифференциал функции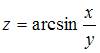 
имеет вид …
- правильно
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
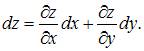
Тогда
6. Приближенное значение функции 
в точке 
вычисленное с помощью полного дифференциала, равно …
0,71
0,41
1,29
0,83
Решение:
Воспользуемся формулой 
где 
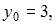
Вычислим последовательно
Тогда
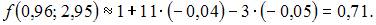
Тема 12: Производная по направлению и градиент
1. Модуль градиента функции нескольких переменных 
в точке 
равен …
- правильно
Решение:
Градиент функции нескольких переменных находится по формуле 
Тогда 
и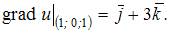 
Следовательно,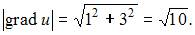 
2. Модуль градиента функции нескольких переменных 
в точке 
равен …
- правильно
Решение:
Градиент функции нескольких переменных находится по формуле
Тогда 
и 
Следовательно, 
3. Производная 
по направлению 
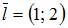функции двух переменных 
в точке 
равна …
- правильно
Решение:
Производная по направлению 
функции двух переменных 
определяется как 
где 
и 
– направляющие косинусы вектора 
.
Вычислим частные производные в точке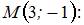 
Определив направляющие косинусы
получаем 
4. Производная 
по направлению 
функции двух переменных 
в точке 
равна …
- правильно
Решение:
Производная по направлению функции двух переменных определяется как где и – направляющие косинусы вектора .
Вычислим частные производные в точке 
Определив направляющие косинусы
получаем 
5. Градиент функции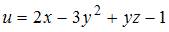 
в точке 
равен …
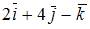- правильно
Решение:
Градиент функции нескольких переменных находится по формуле
Тогда 
и 
6. Градиент функции 
в точке 
равен …
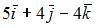- правильно
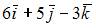
7. Производная по направлению 
функции двух переменных 
в точке 
равна …
– 4,8
– 0,96
Решение:
Производная по направлению 
функции двух переменных определяется как 
где и – направляющие косинусы вектора .
Вычислим частные производные в точке
Определив направляющие косинусы
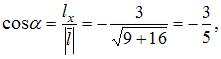
получаем 
Тема 13: Основные методы интегрирования
1. Множество первообразных функции 
имеет вид …
- правильно
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции.
Разложив знаменатель дробно-рациональной функции на линейные множители, получаем
2. Множество первообразных функции 
имеет вид …
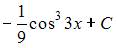- правильно
3. Множество первообразных функции 
имеет вид …
- правильно
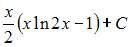
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле 
Тогда
4. Множество первообразных функции 
имеет вид …
- правильно
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
5. Множество первообразных функции 
имеет вид …
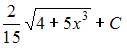- правильно
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
Произведем замену 
6. Множество первообразных функции 
имеет вид …
- правильно
Тема 14: Свойства определенного интеграла
1. Значение определенного интеграла 
принадлежит промежутку …
- правильно
Решение:
Если функция 
интегрируема на 
и 
то 
Определим наименьшее и наибольшее значения функции 
на отрезке 
. Для этого вычислим производную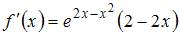 
и решим уравнение 
Тогда 
Вычислив
и 
получаем наименьшее значение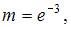 
а наибольшее – 
Следовательно, 
или 
2. Среднее значение функции 
на отрезке 
равно …
- правильно
Решение:
Среднее значение функции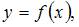 
непрерывной на отрезке 
вычисляется по формуле 
где 
Тогда
3. Для определенного интеграла 
справедливо равенство …
- правильно
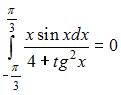
Решение:
Пусть 
Тогда 
то есть функция 
является четной. А определенный интеграл от четной функции по симметричному интервалу 
можно представить как 
4. Значение определенного интеграла 
принадлежит промежутку …
- правильно
Решение:
Если функция интегрируема на 
и то
Определим наименьшее и наибольшее значения функции 
на отрезке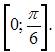 
Так как на этом отрезке справедливо неравенство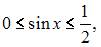 
то с учетом свойств функции 
, можем получить, что 
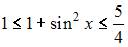и 
То есть наименьшее значение 
а наибольшее – 
Следовательно,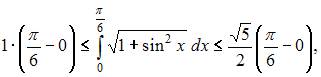 
или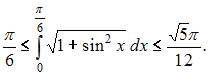 
5. Среднее значение функции 
на отрезке 
равно …
- правильно
6. Если функция непрерывна на отрезке 
то интеграл 
можно представить в виде …
- правильно
7. Определенный интеграл 
равен …
Решение:
Пусть 
Тогда 
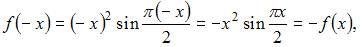то есть функция 
является нечетной. А определенный интеграл от нечетной функции по симметричному интервалу равен нулю.
Тема 15: Методы вычисления определенного интеграла
1. Несобственный интеграл 
…
равен 
равен 
расходится
равен 
2. Определенный интеграл 
равен …
- правильно
