Для виконання роботи необхідно вивчити такий матеріал: явища переносу; теплопровідність.
[ 1, т.1 §§ 15.3; 2, §§ 48; 3, вступ до розд.5, §§ 5.8–5.10; 4, т.1 §§ 112, 113]
Щоб експериментально визначити коефіцієнт теплопровідності l можна використати процес передачі теплоти в твердому тiлi, оскільки закономірності такого процесу завжди пов’язані з коефіцієнтом теплопровідності.
Коефіцієнт теплопровідності можна знайти з основного рівняння, яке описує процес теплопровідності – рівняння Фур’є:
 ,
,
де  – кількість тепла, що передається вздовж осі x крізь елемент площі
– кількість тепла, що передається вздовж осі x крізь елемент площі  за час
за час  при градієнті температури
при градієнті температури  .
.
Звiдси
 .
.
Практичне вимірювання величин, які входять в останнє рівняння, має деякі ускладнення, тому краще розглядати такi процеси, в яких можна легко i точно вимiряти всi величини, що входять до розрахункової формули для визначення  . Один iз таких процесiв – регулярний режим.
. Один iз таких процесiв – регулярний режим.
Нехай нагрiте до деякої температури T тiло розмiщене в середовищi, яке добре проводить тепло (наприклад вода). Температура цього середовища пiдтримується сталою і рівною T 0. Тодi внаслiдок теплопровiдностi рiзниця температур тiла та середовища  постiйно зменшуватиметься i в момент встановлення рiвноваги дорiвнюватиме нулю. Закон цього зменшення, тобто функцiя Δ T = f (t), залежить вiд розмiрiв та форми тiла, його теплофiзичних властивостей, а також вiд того, як було нагрiте тiло (рiвномiрно чи нi) перед початком дослiду. В початковiй стадiї теплообмiну цей закон досить складний.
постiйно зменшуватиметься i в момент встановлення рiвноваги дорiвнюватиме нулю. Закон цього зменшення, тобто функцiя Δ T = f (t), залежить вiд розмiрiв та форми тiла, його теплофiзичних властивостей, а також вiд того, як було нагрiте тiло (рiвномiрно чи нi) перед початком дослiду. В початковiй стадiї теплообмiну цей закон досить складний.
З часом настає так званий регулярний режим нагрiвання (чи охолодження), при якому рiзниця температур мiж будь-якою точкою зразка та навколишнiм середовищем залежить вiд часу за законом:
 . (2.2.1)
. (2.2.1)
Величина a у формулі (2.2.1) називається темпом нагрiвання (чи охолодження) i пов’язана з властивостями тiла:
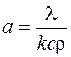 , (2.2.2)
, (2.2.2)
де k – коефiцiєнт форми, що залежить вiд форми та розмiрiв тiла; c – питома теплоємнiсть тiла; r – густина тiла. Для цилiндра:
 , (2.2.3)
, (2.2.3)
де R, h – вiдповiдно радiус i висота цилiндра.
 Таким чином, визначення коефiцiєнта теплопровідностi l цилiндричного зразка з вiдомими густиною речовини r та питомою теплоємнiстю c зводиться до визначення темпу нагрiвання а. З цiєю метою вимiрюють рiзницю температур мiж зразком i зовнiшнiм середовищем у рiзнi моменти часу.
Таким чином, визначення коефiцiєнта теплопровідностi l цилiндричного зразка з вiдомими густиною речовини r та питомою теплоємнiстю c зводиться до визначення темпу нагрiвання а. З цiєю метою вимiрюють рiзницю температур мiж зразком i зовнiшнiм середовищем у рiзнi моменти часу.
Згiдно з (2.2.1)
 . (2.2.4)
. (2.2.4)
|
 після настання регулярного режиму на графіку має вигляд прямої з кутовим коефіцієнтом а (рис. 2.2.1).
після настання регулярного режиму на графіку має вигляд прямої з кутовим коефіцієнтом а (рис. 2.2.1).
Щоб знайти темп нагрівання а,
на прямолiнiйнiй ділянці графіка вибирають довільно (але на досить ве-
ликій відстані одна від одної) точки 1 i 2. Для цих точок визначають моменти часу τ1 та τ2, а також відповідні їм значення логарифмів різниці температур lnΔ T 1 i lnΔ T 2.
Тодi темп нагрівання розраховується за формулою:
 . (2.2.5)
. (2.2.5)
Пiсля визначення темпу нагрiвання можна знайти коефiцiєнт теплопровiдностi:
 . (2.2.6)
. (2.2.6)
За середовище, в якому нагрiвається зразок, доцiльно взяти воду, яка кипить, оскiльки, по-перше, в цьому разi забезпечується достатнiй теплообмiн поверхнi зразка з водою за рахунок перемiшування, по-друге, температура води, що кипить, вiдома та не змiнюється, коли зразок нагрiвається.
Температуру вимiрюють за допомогою диференцiальної термопари та потенцiометра постiйного струму або самозаписувача.
Хiд роботи
1. Ознайомитися з установкою. Увiмкнути нагрiвник та довести воду у посудинi до кипiння. Пiдтримувати температуру води протягом усього дослiду.
2. Вимiряти радіус R та висоту зразка h. За формулою (2.2.3) обчислити коефiцiєнт форми k.
3. 
 Занурити цилiндр у воду та увiмкнути самозаписувач. Протягом 15-20 хв отримати діаграму залежності температури зразка від часу
Занурити цилiндр у воду та увiмкнути самозаписувач. Протягом 15-20 хв отримати діаграму залежності температури зразка від часу  (рис.2.2.2).
(рис.2.2.2).
4. Для визначення темпу нагрівання опрацювати діаграмну стрічку. Для цього:
а) нанести на діаграму шкалу температур (мінімальна температура зразка – кімнатна, а максимальна – 100 оС);
б) знаючи швидкість руху діаграмної стрічки, нанести на діаграму шкалу часу;
в) через кожні 120 с одержати значення температури зразка t оС. Значення температури та часу занести до таблиці 2.2.1.
5. Розрахувати різницю між температурою зразка та киплячою водою (Т 0 = 100 ºС)  і занести її в табл. 2.2.1.
і занести її в табл. 2.2.1.
6. Побудувати графік залежності  .
.
7. За формулою (2.2.5) визначити темп нагрівання а.
8. За формулою (2.2.6) розрахувати коефіцієнт теплопровідності ебоніту  .
.
Таблиця 2.2.1
| № пор. | 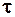 , с , с
| t оC | ∆ T, K | ln ∆ T |  , Вт/(м∙К) , Вт/(м∙К)
|
Темп нагріву зразка а можна визначити дещо змінюючи засіб обробки температурної залежності зразка від часу  .
.
 При всякому відображенні температури на папері (машинному: автоматичний вимір і друк температури за допомогою самописців або ручному: побудова діаграм і графіків) виконується співвідношення пропорційної залежності між значенням температури Т і значенням координати l, яка відповідає цьому значенню температури (рис. 2.2.3).
При всякому відображенні температури на папері (машинному: автоматичний вимір і друк температури за допомогою самописців або ручному: побудова діаграм і графіків) виконується співвідношення пропорційної залежності між значенням температури Т і значенням координати l, яка відповідає цьому значенню температури (рис. 2.2.3).
Тобто:
 ~
~ 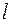 ;
;  ;
; 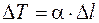 ;
;  .
.
Різниця логарифмів

відповідає логарифму відношення
 .
.
Коефіцієнт пропорційності  скорочується і відношення температур відповідає відношенню координат.
скорочується і відношення температур відповідає відношенню координат.
Обробка графіка залежності температури зразка від часу  виконується у такій послідовності:
виконується у такій послідовності:
1. Для кожного з вибраних значень часу  виміряти лінійкою різницю координат, які відповідають температурі киплячої води та температурі зразка
виміряти лінійкою різницю координат, які відповідають температурі киплячої води та температурі зразка  , де Δ l T1 відповідно TК – T1 (рис. 2.2.4).
, де Δ l T1 відповідно TК – T1 (рис. 2.2.4).
 2. Отримані значення різниць (
2. Отримані значення різниць ( ;
;  ;
; 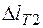 ;...), виміряних в мм, прологарифмувати:
;...), виміряних в мм, прологарифмувати:
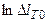 ;
;  ;
; 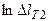 ;....
;....
3. На підставі значень часу 0, τ1, τ2,… і відповідних значень  , побудувати графік залежності
, побудувати графік залежності  . Лінію графіка визначити прямою лінією. Зовнішній вигляд графіка співпадає з рисунком 2.2.1.
. Лінію графіка визначити прямою лінією. Зовнішній вигляд графіка співпадає з рисунком 2.2.1.
4. На графіку вибрати дві точки на початку і в кінці досліду. По вибраних точках визначити значення їх координат.
5. Використовуючи данні обробки графіка, визначити темп нагрівання за формулою:
 .
.
Контрольні запитання
1. Які явища переносу Вам відомі?
2. Дайте означення явища теплопровідності.
3. Запишіть закон Фур’є для теплопровідності.
4. Що називається коефіцієнтом теплопровідності? Його фізичний зміст.
5. Від чого залежить теплопровідність тіл?
6. Дайте означення градієнта температури.
7. Поясніть фізичний зміст знака мінус („-”) в законі Фур’є.
8. Що таке регулярний режим нагрівання? Запишіть закон зміни температури від часу при регулярному режимі.
9. Поясніть практичне значення коефіцієнта теплопровідності будівельних матеріалів.






