| t, мин | 0,5 | ||||||||
m  мг* мг*
| 2–1 | ||||||||
Q  % %
| 20,0 | 27,5 | 37,5 | 52,5 | 65,0 | 72,5 | 85,0 | 95,0 | 100,0 |
* m  – масса осадка без чашечки весов.
– масса осадка без чашечки весов.
Условия опыта: h = 0,09 м;  = 1 • 10
= 1 • 10  3 Па с;
3 Па с;
 = 2,72 • 103 кг/м3;
= 2,72 • 103 кг/м3;  = 1,00 • 103 кг/м3.
= 1,00 • 103 кг/м3.
Очевидно, что абсолютные массы осадка в разные моменты времени будут зависеть от исходной массы, поэтому рассчитывают относительные массы в процентах от исходной массы. Из данных таблицы 15.1 видно, что начиная с 18 – й минуты масса осадка на чашечках весов не изменяется, следовательно, к этому моменту времени выпал весь осадок, его массу принимают за максимальную:
 = 40 мг.
= 40 мг.
 В нижней строке таблицы указаны относительные массы выпавшего осадка (Q
В нижней строке таблицы указаны относительные массы выпавшего осадка (Q  , %) в соответствующие моменты времени: Q=
, %) в соответствующие моменты времени: Q=  100%. Строим седиментационную кривую Q=f (t) (рис 15.5)
100%. Строим седиментационную кривую Q=f (t) (рис 15.5)
Из графика видно, что чем дольше идет осаждение, тем меньше прирост массы осадка. В начальный момент времени частицы разных размеров равномерно распределены в жидкости (перед началом эксперимента суспензия тщательно перемешивается). Чем крупнее частица, тем быстрее она оседает, но мелкие частицы, находящиеся вблизи чашечки весов, осядут скорее, чем крупные, находящиеся у поверхности жидкости, т.е, на расстоянии h от чашечки весов. В результате на чашечке весов будут собираться частицы всех размеров. Поэтому кривая седиментации всегда начинается с прямолинейной зависимости и выходит из начала координат.
Однако через некоторое время t  ,нужное, чтобы самые крупные частицы прошли расстояние h, этих частиц в Суспензии не останется. Поэтому в дальнейшем прирост массы осадка уменьшится – линия станет кривой, выпуклой к оси ординат. Время t
,нужное, чтобы самые крупные частицы прошли расстояние h, этих частиц в Суспензии не останется. Поэтому в дальнейшем прирост массы осадка уменьшится – линия станет кривой, выпуклой к оси ординат. Время t  дает возможность рассчитать радиус самой крупной частицы:
дает возможность рассчитать радиус самой крупной частицы:
r 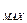 =K
=K  ,
,
где K=  .
.
Рассчитаем значение постоянной К, подставив в уравнение данные из условий опыта:


Определим единицы измерения К. Так как

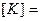
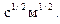
По графику (рис. 15.5) находим t min = 0,2 мин. Тогда


В дальнейшем скорость накопления осадка будет уменьшаться, график будет оставаться криволинейным вплоть до установления постоянной массы осадка. В нашем примере это произойдет через t max =18 мин. Такое время потребовалось, чтобы самая маленькая частица, имеющая радиус rmin с поверхности жидкости осела на чашечку весов, т. е, прошла расстояние h.
Теперь мы можем рассчитать радиус самой мелкой частицы:
r min =K 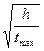 =
= 
 =
= 
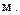
Таким образом, мы установили минимальный и максимальный радиусы частиц. Теперь важно установить, в каком соотношении присутствуют частицы разных размеров, т.е. установить фракционный состав порошка. Для этого на основе седиментационной кривой надо построить интегральную и дифференциальную кривые распределения частиц.
Построение интегральной кривой распределения Qo,i = f(r). Общее количество порошка, осевшего к произвольному моменту времени t 1 равно Q 1. Проведем касательную к кривой в этой точке. Она отсечет на оси ординат отрезок Q0,t Ордината Q1 окажется разделенной на две части: Q0,1 – масса частиц во фракциях, нацело выпавших к моменту t1 и g1 – масса частиц во фракциях, выпавших лишь частично: Q1= Q0,1 + g1
Рассчитаем радиус частиц, прошедших за время t1 всю высоту суспензии до чашечки весов:  =
= 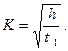
Следовательно, Q0,1 – это масса частиц, имеющих радиусы  . Аналогично Q0,2 – масса порошка, радиусычастиц которого
. Аналогично Q0,2 – масса порошка, радиусычастиц которого 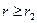 ,
,  =
=  .
.
Обычно касательные проводят к наиболее выпуклым точкам кривой седиментации. Однако часто их проводят к точкам, отвечающим моментам времени, когда измерялась масса осадка. Все необходимые данные для построения кривых распределения приведены в таблице 15.2.
На рис. 15.6 представлена интегральная кривая распределения. Каждая ордината указывает процентное содержание частиц, обладающих радиусом, равным или больше указанного на оси абсцисс.
Интегральная кривая распределения позволяет определить процентное содержание фракций. Например; для фракции, содержащей частицы с радиусами от  до
до  , оно равно
, оно равно 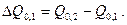
Таблица 15,2
Результаты обработки данных седиментации талька в воде
t  , мин , мин
| Q  ,% ,%
| Qo,i,% | r  *м *м
| 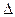 Qo,i,% Qo,i,%
| 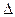 r r  м м
| 
| r  м м
|
| 0,5 | 20,0 | 9,0 | 2,83 | 9,0 | 1,64 | 3,65 | |
| 27,5 | 14,5 | 2,00 | 5,5 | 0,83 | 6,63 | 2,42 | |
| 37,5 | 19,5 | 1,41 | 5,0 | 0,59 | 8,5 | 1,71 | |
| 52,5 | 25,5 | 1,00 | 6,0 | 0,41 | 14,6 | 1,21 | |
| 65,0 | 37,0 | 0,82 | 11,5 | 0,18 | 63,9 | 0,91 | |
| 72,5 | 42,5 | 0,71 | 5,5 | 0,11 | 50,0 | 0,77 | |
| 85,0 | 51,6 | 0,58 | 9,1 | 0,13 | 70,0 | 0,65 | |
| 95,0 | 57,8 | 0,50 | 6,2 | 0,08 | 77,5 | 0,54 | |
| 0,47 | 42,2 | 0,03 | 0,49 |

Наглядное представление о
распределении частиц по размерам
дает дифференциальная кривая распре –
деления.
Построение дифференциальной
кривой распределения F% = f(r).
Дифференциальная кривая распределе –
ния частиц представляет собой зависи –
мость массовой функции распределения
 радиуса частиц.
радиуса частиц.
Для построения графика функц –
ии F% = f(r) можно использовать инте –
гральную кривую, определяя приращение
 для серий фракций
для серий фракций  . Полученное значение F относят к среднему для данной фракции радиусу.
. Полученное значение F относят к среднему для данной фракции радиусу.
Дифференциальную кривую можно построить и непосредственно из кривой седиментации, определяя  как отрезки, отсекаемые соседними касательными на оси ординат, например,
как отрезки, отсекаемые соседними касательными на оси ординат, например, 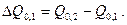 Для нахождения
Для нахождения  необходимо определить радиусы частиц, осевших к моментам времени t 1и t 2.
необходимо определить радиусы частиц, осевших к моментам времени t 1и t 2.
Воспользуемся таблицей 15.2. Столбец 5 в ней 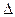 Qo,i – разница масс фракций, полностью осевших к определенным моментам времени.
Qo,i – разница масс фракций, полностью осевших к определенным моментам времени.
Столбец 6 – разница радиусов наименьших частиц в этих фракциях.
Столбец 7 – значение функции.
Столбец 8 – средний радиус данной фракции, именно к нему относят F.
Например, 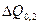 = 14,5 – 9,0 = 5,5;
= 14,5 – 9,0 = 5,5;  = (2,38 – 2,00) • 10
= (2,38 – 2,00) • 10  5 = 0,83 • 10
5 = 0,83 • 10 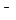 5
5
r ср.2 = 
 0,3 = 19,5 - 14,5 = 5,0;
0,3 = 19,5 - 14,5 = 5,0;
 3 = (2,00 – 1,41) • 10
3 = (2,00 – 1,41) • 10 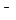 5 = 0,59 • 10
5 = 0,59 • 10 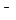 5
5
r ср.3 =  = 1,71 • 10
= 1,71 • 10 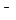 5 и т.д.
5 и т.д.

Дифференциальная кривая представлена
на рис. 15.7.
Площадь под всей кривой равна
массе всех частиц в системе (100%).
Радиус, отвечающий максимуму на
кривой, показывает, какого радиуса
частицы наиболее распространены в
данной системе. Чем более четко вы –
ражен максимум на кривой, тем более
неравномерно распределены частицы по
размерам. Для того чтобы определить
процентное содержание фракций частиц
с заданными радиусами, надо провести
вертикаль до пересечения с кривой.
Площади под кривой, ограниченные
этими линиями, характеризуют процентное содержание соответствующих фракций.
В результате седиментационного анализа данной системы мы установили, что
1) минимальный радиус частиц составляет 0,47 • 10 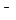 5 м;
5 м;
2) максимальный радиус равен 4,47 • 10  5 м;
5 м;
8) процентное содержание отдельных фракций с радиусом частиц:
 • от 0,47 • 10
• от 0,47 • 10 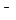 5м до 1,0 • 10
5м до 1,0 • 10 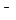 5м составляет 72,5%;
5м составляет 72,5%;
11Указаны значения самого маленького радиуса среди частиц, полностью выпавших в осадок к данному моменту.
• от 1,0 • 10 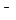 5м до 1,5 • 10
5м до 1,5 • 10 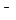 5 м составляет 10%;
5 м составляет 10%;
• от 1,5 • 10 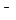 5 м до 2,0 • 10
5 м до 2,0 • 10 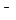 5 м составляет 4%;
5 м составляет 4%;
• от 2,0 • 10 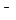 5 м до 2,5 • 10
5 м до 2,5 • 10 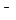 5 м составляет 3%;
5 м составляет 3%;
• больше 2,5 • 10 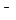 5м составляет 10,5%.
5м составляет 10,5%.






