Санкт-Петербург
Методические указания к выполнению контрольных работ
1. За время обучения физике студент должен выполнить четыре контрольные работы.
2. Каждые два варианта (1 и 2, 3 и 4) содержат пять задач.
3. Каждую контрольную работу надо выполнять в отдельной школьной тетради, на обложке которой указать номер контрольной работы, наименование дисциплины (физика), фамилию и инициалы студента, номер зачетной книжки, номер группы (для студентов дневной и вечерней форм обучения), домашний адрес (для студентов заочной формы обучения).
4. Контрольную работу следует выполнять аккуратно, оставляя поля для замечаний преподавателя.
5. Задачи своего варианта переписывать полностью, а заданные физические величины выписать отдельно, при этом все числовые величины должны быть выражены в СИ.
6. Для пояснения решения задачи, где это нужно, аккуратно сделать чертеж.
7. Решения задач и используемые формулы должны сопровождаться пояснениями.
8. Приводить вывод расчетной формулы, которая нужна для решения конкретной задачи.
9. Решение задачи рекомендуется сначала сделать в общем виде, т. е. только в буквенных обозначениях.
10.Вычисления следует проводить путем подстановки заданных величин в расчетную формулу.
11. Проверить размерность полученных величин по расчетной формуле и тем самым подтвердить ее правильность.
Контрольные работы, представленные без соблюдения вышеперечисленных указаний, зачитываться не будут.
При представлении работы на повторную проверку обязательно предъявлять первоначальную работу с замечаниями преподавателя.
Методические рекомендации студентам при самостоятельной подготовке к экзаменам
1. Сначала необходимо изучить данное определение и аналитическую запись рассматриваемого закона. При этом необходимо знать физический смысл всех входящих в формулу букв и символов, знать их размерность.
2. Запомнить самый простой, пусть даже не совсем корректный вид формулы данного закона, а затем научиться усложнять его до полной точной формулировки в аналитическом виде.
3. Для улучшения запоминания формулы уметь видеть и находить сходство в записи различных законов, например, кинетическая энергия поступательного и вращательного движений и энергия заряженного конденсатора записываются одинаково.
4. На простых, качественных примерах рассмотреть основные положения данного закона, что способствует запоминанию и пониманию его формулировки. Примеры дает лектор, либо необходимо их придумать самому. Подобные задачи составляют систему опорных сигналов, облегчающих понимание и запоминание закона.
5. Не продолжать разбирать лекции, если возник вопрос, на который нет ответа. Искать ответ либо в конспекте (лучше додуматься самостоятельно), либо использовать дополнительную литературу, но обязательно ответить на этот вопрос, даже если на это уйдет много времени. В крайнем случае, задать этот вопрос на консультации перед экзаменом. Не пропускать консультации.
6. При разборе лекции все математические действия должны быть полностью понятными. Уметь задавать себе вопросы, которые содержатся в лекции в неявном виде. И уметь отвечать на эти вопросы.
7. По возможности не пропускать лекции, даже если есть способ иметь потом конспект на руках. На лекции следить за логикой рассуждений, а не записывать автоматически без понимания.
8. Уметь видеть общие положения, с которых всегда начинается рассмотрение нового вопроса или задачи.
Примеры решения задач
| Пример 1.При фотоэффекте с платиновой поверхности электроны полностью задерживаются разностью потенциалов Uз = 0,8 В. Найти длину волны l используемого облучения. | ||
| Дано: Uз = 0,8 В | Решение Из формулы Эйнштейна для фотоэффекта следует | |
| l =? |

| |
или, с учетом формулы
 имеем
имеем
 ,
откуда ,
откуда
 (Из справочника мы взяли для платины А = 5,29 эВ)
(Из справочника мы взяли для платины А = 5,29 эВ)
| ||
Пример 2.Частица движется со скоростью  , где a = 1 м/с2. Найти средние значения скорости , где a = 1 м/с2. Найти средние значения скорости  и ее модуля и ее модуля 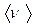 за промежуток времени от t1 =1c до t2 =3c. за промежуток времени от t1 =1c до t2 =3c.
| ||
Дано:
 a = 1 м/с2
t1 = 1c
t2 = 3c
a = 1 м/с2
t1 = 1c
t2 = 3c
| Решение
Среднее значение скалярной или векторной величины a(t) за промежуток времени t2 - t1 находят по формуле
 , (2.1) , (2.1)
| |
 -? -?
 -? -?
| где a(t) – зависимость физической величины от времени. Среднее значение скорости найдем по формуле | |

|  , (2.2)
где , (2.2)
где  - зависимость скорости от времени. По условию задачи - зависимость скорости от времени. По условию задачи  . (2.3)
Подставляя выражение (2.3) в соотношение (2.2), находим . (2.3)
Подставляя выражение (2.3) в соотношение (2.2), находим
 Среднее значение модуля скорости
Среднее значение модуля скорости  найдем по формуле (2.1), подставив найдем по формуле (2.1), подставив 
 Ответ:
Ответ:  (м/с), (м/с), 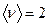 м/с. м/с.
| |
| Пример 3.В баллоне объемом V = 10 л находится гелий под давлением Р1 = 1 М Па и при температуре Т1 = 300 К. После того, как из баллона было выпущено М = 10 г гелия, температура в баллоне понизилась до Т2 = 290 К. Определить давление Р2 гелия, оставшегося в баллоне. | ||
| Дано: V = 10 л P1 = 1 МПа Т1 = 300 К М = 10 г Т2 = 290 К | Решение
Запишем уравнения состояния идеального газа до выпуска газа
 (3.1)
и после выпуска газа (3.1)
и после выпуска газа
| |
| P2 =? | 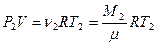 , (3.2) , (3.2)
| |
где М1 и М2 – масса гелия в баллоне до и после выпуска соответственно.
Так как по условию задачи М2 =М1 – М, перепишем уравнение (2.2) в виде
  . (3.3)
Решим систему уравнений (3.1) и (3.3) относительно искомого давления Р2. . (3.3)
Решим систему уравнений (3.1) и (3.3) относительно искомого давления Р2.
 . .
 Ответ: Р2 = 0,36 МПа.
Ответ: Р2 = 0,36 МПа.
| ||
| Пример 4. Два точечных электрических заряда q1 = 1 нКл и q2 = -2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Определить напряженность Е электрического поля, создаваемого этими зарядами в точке, удаленной от заряда q1 на расстояние r1 = 9 см и от заряда q2 на r2 = 7 см. | ||
| Дано: q1 = 1 нКл q2 = -2 нКл d = 10 см r1 = 9 см r2 = 7 см | Решение
Согласно принципу суперпозиции электрических полей напряженность поля, создаваемого зарядами q1 и q2 в интересующей нас точке
 . (4.1) . (4.1)
| |
| Е -? | ||
 Рис. 4.1
Из рис. 4.1 видно, что по теореме косинусов
Рис. 4.1
Из рис. 4.1 видно, что по теореме косинусов
 , (4.2) , (4.2)
 . (4.3)
Из выражения (4.3) найдем . (4.3)
Из выражения (4.3) найдем
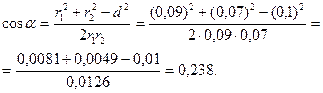 (4.4) (4.4)
 Кроме того,
Кроме того,
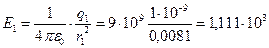 В/м, (4.5) В/м, (4.5)
 В/м. (4.6)
Подставляя числовые значения (4.4), (4.5) и (4.6) в соотношение (4.2), получаем В/м. (4.6)
Подставляя числовые значения (4.4), (4.5) и (4.6) в соотношение (4.2), получаем  В2/м2.
Откуда В2/м2.
Откуда
 В/м = 3,57 кВ/м.
Ответ: В/м = 3,57 кВ/м.
Ответ:  кВ/м. кВ/м.
| ||
Контрольные задания 1 - 2
Вариант 1
1.  Зависимость радиус–вектора частицы от времени дается законом
Зависимость радиус–вектора частицы от времени дается законом  , где a и b – положительные постоянные. Найти уравнение траектории в параметрической форме x = x(t), y = y(t).
, где a и b – положительные постоянные. Найти уравнение траектории в параметрической форме x = x(t), y = y(t).
2.  Обруч и диск одинаковых масс m1 = m2 = m катятся без скольжения с одной и той же скоростью v. Кинетическая энергия обруча Т1= 39,24 Дж. Найти кинетическую энергию Т2 диска.
Обруч и диск одинаковых масс m1 = m2 = m катятся без скольжения с одной и той же скоростью v. Кинетическая энергия обруча Т1= 39,24 Дж. Найти кинетическую энергию Т2 диска.
3.  На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М = 60 кг, масса доски m = 20 кг. Найти, на какое расстояние d передвинется тележка, если человек перейдет на другой конец доски. Длина доски l = 2 м. Массой колес пренебречь. Трение не учитывать.
На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М = 60 кг, масса доски m = 20 кг. Найти, на какое расстояние d передвинется тележка, если человек перейдет на другой конец доски. Длина доски l = 2 м. Массой колес пренебречь. Трение не учитывать.
4.  Уравнение затухающих колебаний дано в виде
Уравнение затухающих колебаний дано в виде  . Найти скорость v колеблющейся частицы в момент t = 4Т, где Т – период колебаний.
. Найти скорость v колеблющейся частицы в момент t = 4Т, где Т – период колебаний.
5.  Считая, что температура и молярная масса воздуха, а также ускорение свободного падения не зависят от высоты, найти разность высот, на которых плотности воздуха при температуре 0оС отличаются в «e» раз.
Считая, что температура и молярная масса воздуха, а также ускорение свободного падения не зависят от высоты, найти разность высот, на которых плотности воздуха при температуре 0оС отличаются в «e» раз.
Контрольные задания 3 - 4
Вариант 1
1.  Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут равномерно распределенные заряды соответственно q1 = 1 нКл и q2 = -0,5 нКл. Найти напряженность поля в точке, отстоящей от центра сфер на расстоянии r = 9 см, используя теорему Гаусса.
Две концентрические проводящие сферы радиусами R1 = 6 см и R2 = 10 см несут равномерно распределенные заряды соответственно q1 = 1 нКл и q2 = -0,5 нКл. Найти напряженность поля в точке, отстоящей от центра сфер на расстоянии r = 9 см, используя теорему Гаусса.
2.  Какая мощность выделяется в единице объема проводника длиной l = 0,2 м, если на его концах поддерживается разность потенциалов U = 4 В? Удельное сопротивление проводника r = 1 мкОм×м.
Какая мощность выделяется в единице объема проводника длиной l = 0,2 м, если на его концах поддерживается разность потенциалов U = 4 В? Удельное сопротивление проводника r = 1 мкОм×м.
3.  Проводник имеет форму бесконечно длинного цилиндра с внешним радиусом R1 и внутренним радиусом R2. Текущий по такому проводнику ток J равномерно распределен по его сечению. Определить индукцию. В магнитного поля в точках на расстоянии r < R2 от оси цилиндра.
Проводник имеет форму бесконечно длинного цилиндра с внешним радиусом R1 и внутренним радиусом R2. Текущий по такому проводнику ток J равномерно распределен по его сечению. Определить индукцию. В магнитного поля в точках на расстоянии r < R2 от оси цилиндра.
4. Найти длину волны де Бройля l для пучка протонов, прошедших ускоряющую разность потенциалов Dj = 100 В.
5. Фотон с длиной волны l = 6 пм рассеялся под прямым углом на покоившемся свободном электроне. Найти частоту рассеянного фотона.
Контрольные задания 1 - 2
Вариант 2
1.  Зависимость радиус – вектора частицы от времени дается законом
Зависимость радиус – вектора частицы от времени дается законом  , где a и b – положительные постоянные. Найти уравнение траектории в виде зависимости y(x).
, где a и b – положительные постоянные. Найти уравнение траектории в виде зависимости y(x).
2.  Однородный цилиндр радиусом R = 0,2 м и массой m = 5 кг вращается вокруг своей оси. Зависимость угловой скорости w вращения цилиндра от времени t дается уравнением w = A + Bt, где В = 8 рад/с2. Найти касательную силу F, приложенную к боковой поверхности цилиндра перпендикулярно его оси.
Однородный цилиндр радиусом R = 0,2 м и массой m = 5 кг вращается вокруг своей оси. Зависимость угловой скорости w вращения цилиндра от времени t дается уравнением w = A + Bt, где В = 8 рад/с2. Найти касательную силу F, приложенную к боковой поверхности цилиндра перпендикулярно его оси.
3.  В лодке массой М = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью
В лодке массой М = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью 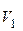 = 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью
= 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью 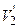 = 4 м/с относительно лодки. Найти скорость U движения лодки после прыжка человека, если прыжок совершен в сторону, противоположную движению лодки.
= 4 м/с относительно лодки. Найти скорость U движения лодки после прыжка человека, если прыжок совершен в сторону, противоположную движению лодки.
4.  Частица массой m = 5 г гармонически колеблется с частотой n = 5 Гц и амплитудой А = 3 см. Найти модуль скорости v частицы в момент времени, когда ее смещение x = 1,5 см.
Частица массой m = 5 г гармонически колеблется с частотой n = 5 Гц и амплитудой А = 3 см. Найти модуль скорости v частицы в момент времени, когда ее смещение x = 1,5 см.
5.  Пусть h0 – отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а h – соответствующее отношение на высоте h = 3000 м. Найти отношение h/h0 при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты.
Пусть h0 – отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а h – соответствующее отношение на высоте h = 3000 м. Найти отношение h/h0 при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты.
Контрольные задания 3 - 4
Вариант 2
1.  Расстояние между точечными зарядами +32 мкКл и -32 мкКл равно 12 см. Определить напряженность поля в точке, удаленной на 8 см как от первого, так и от второго заряда.
Расстояние между точечными зарядами +32 мкКл и -32 мкКл равно 12 см. Определить напряженность поля в точке, удаленной на 8 см как от первого, так и от второго заряда.
2.  В проводнике за промежуток времени Dt = 10 c при равномерном возрастании силы тока от J1 = 1 А до J2 = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.
В проводнике за промежуток времени Dt = 10 c при равномерном возрастании силы тока от J1 = 1 А до J2 = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.
3.  По бесконечному прямому полому круговому цилиндру параллельно оси цилиндра проходит постоянный ток силой J = 30 А, который равномерно распределен по его поверхности. Найти магнитную индукцию В в точке вне цилиндра, находящейся на расстоянии r = 20 см от его оси.
По бесконечному прямому полому круговому цилиндру параллельно оси цилиндра проходит постоянный ток силой J = 30 А, который равномерно распределен по его поверхности. Найти магнитную индукцию В в точке вне цилиндра, находящейся на расстоянии r = 20 см от его оси.
4. Фотоэлектрический порог для некоторого металла l0 = 275 нм. Найти максимальную скорость vm электронов, вырываемых из металла светом с длиной волны l = 180 нм.
5. Черное тело имеет температуру Т1 = 500 К. Какова будет температура Т2 этого тела, если в результате его нагревания поток Ф излучения увеличится в n = 5 раз?
Контрольные задания 1 - 2
Вариант 3
1.  Радиус-вектор частицы определяется выражением
Радиус-вектор частицы определяется выражением  . Вычислить путь S, пройденный частицей за первые 10 с движения.
. Вычислить путь S, пройденный частицей за первые 10 с движения.
2.  Сила
Сила  , Н приложена к частице, радиус-вектор которой
, Н приложена к частице, радиус-вектор которой 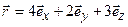 , м. Найти момент силы
, м. Найти момент силы  относительно начала координат.
относительно начала координат.
3.  Шар без трения скатывается с наклонной плоскости высотой h = 90 см. Найти его скорость у основания наклонной плоскости.
Шар без трения скатывается с наклонной плоскости высотой h = 90 см. Найти его скорость у основания наклонной плоскости.
4.  Записать выражение для плоской волны с амплитудой А, частотой w, длиной волны l и начальной фазой p/4, распространяющейся в непоглощающей среде вдоль оси y.
Записать выражение для плоской волны с амплитудой А, частотой w, длиной волны l и начальной фазой p/4, распространяющейся в непоглощающей среде вдоль оси y.
5. Один моль кислорода, находившегося при температуре Т1 = 290 К, адиабатически сжали так, что его давление возросло в h раз. Найти работу, которая была совершена над газом.
Контрольные задания 3 – 4
Вариант 3
1. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда d. Определить напряженность Е электрического поля этой плоскости. Использовать теорему Гаусса.
2. Сила тока в проводнике изменяется со временем по закону J = 4 + 2t. Какое количество электричества проходит через поперечное сечение проводника за промежуток времени от t1 = 1 c до t2 = 4 с?
3. В магнитном поле, индукция которого изменяется по закону B = a + bt2, где a = 0,1 Тл, b = 0,01 Тл/с, расположена квадратная рамка со стороной a = 20 см, причем плоскость рамки перпендикулярна вектору 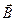 . Определить ЭДС. индукции в рамке в момент времени t = 5 с.
. Определить ЭДС. индукции в рамке в момент времени t = 5 с.
4. Найти длину волны де Бройля l для электрона, имеющего кинетическую энергию Т = 1 МэВ.
5. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, lm = 580 нм. Найти энергетическую светимость  поверхности тела.
поверхности тела.
Контрольные задания 1 - 2
Вариант 4
1. Радиус – вектор частицы меняется со временем по закону
 , где a и b – положительные постоянные. Найти уравнение траектории частицы y(x).
, где a и b – положительные постоянные. Найти уравнение траектории частицы y(x).
2.  Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси z, проходящей через его центр. Уравнение вращения шара имеет вид j = А + Вt2 + Ct3, где В = 4 рад/с2, С = -1 рад/с3. Определить момент сил Мz в момент времени t = 2 c.
Шар массой m = 10 кг и радиусом R = 20 см вращается вокруг оси z, проходящей через его центр. Уравнение вращения шара имеет вид j = А + Вt2 + Ct3, где В = 4 рад/с2, С = -1 рад/с3. Определить момент сил Мz в момент времени t = 2 c.
3.  Частица массой 1 г, двигавшаяся со скоростью
Частица массой 1 г, двигавшаяся со скоростью  , испытала абсолютно неупругое столкновение с другой частицей, масса которой 2 г и скорость
, испытала абсолютно неупругое столкновение с другой частицей, масса которой 2 г и скорость  . Найти скорость
. Найти скорость  образовавшейся частицы.
образовавшейся частицы.
4.  Найти круговую частоту w гармонических колебаний частицы, если при смещении х1 и х2 от положения равновесия ее скорости равны v1 и v2 соответственно.
Найти круговую частоту w гармонических колебаний частицы, если при смещении х1 и х2 от положения равновесия ее скорости равны v1 и v2 соответственно.
5.  В сосуде объемом V = 2 м3 находится смесь гелия массой М1 = 4 кг и водорода массой М2 = 2 кг при температуре t = 27 оС. Определить молярную массу и давление смеси газов.
В сосуде объемом V = 2 м3 находится смесь гелия массой М1 = 4 кг и водорода массой М2 = 2 кг при температуре t = 27 оС. Определить молярную массу и давление смеси газов.
Контрольные задания 3 - 4
Вариант 4
1. Два точечных заряда q1 = 7,5 нКл и q2 = -14,7 нКл расположены на расстоянии l = 5 см. Найти напряженность электрического поля в точке, находящейся на расстоянии а=3 см от положительного заряда и на расстоянии b = 4 см от отрицательного заряда.
2. В медном проводнике объемом V = 6 см3 при прохождении по нему постоянного тока за время t = 1 мин выделилось количество теплоты Q = 216 Дж. Вычислить напряженность электрического поля в проводнике.
3. Протон и электрон, имеющие равные скорости, попадают в однородное магнитное поле перпендикулярно его направлению. Во сколько раз радиус кривизны траектории движения протона в этом магнитном поле больше радиуса кривизны траектории электрона?
4. Температура черного тела изменилась при его нагревании от 1000 до 3000 К. Во сколько раз увеличилась при этом энергетическая светимость тела  ?
?
5. Найти задерживающую разность потенциалов Uз для электронов, вырываемых при освещении калия светом с длиной волны l = 330 нм.
Контрольные задания 1 - 2
Вариант 5
1.  Радиус-вектор частицы определяется выражением
Радиус-вектор частицы определяется выражением  (м). Вычислить модуль перемещения за первые 10 с движения.
(м). Вычислить модуль перемещения за первые 10 с движения.
2. Первоначальная энергия тела Е1 = 10 Дж, конечная энергия Е2 = 8 Дж. Найти приращение энергии DЕ.
3.  Человек массой m стоит на краю горизонтального, однородного диска массой М, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент времени человек начал двигаться по краю диска и совершил перемещение на угол
Человек массой m стоит на краю горизонтального, однородного диска массой М, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент времени человек начал двигаться по краю диска и совершил перемещение на угол  относительно диска, после чего остановился. Пренебрегая размерами человека, найти угол
относительно диска, после чего остановился. Пренебрегая размерами человека, найти угол  , на который повернулся диск относительно неподвижной системы отсчета к моменту остановки человека.
, на который повернулся диск относительно неподвижной системы отсчета к моменту остановки человека.
4. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению движения электрона. Скорость электрона v = 4 ∙ 107 м/с. Индукция магнитного поля В = 1 мТ. Найти тангенциальное аτ и нормальное аn ускорение электрона в магнитном поле.
5. В баллоне объемом V = 10 л находится гелий под давлением Р1 = 1 МПа и при температуре Т1 = 300 К. После того как из баллона было выпущено М = 10 г гелия, температура в баллоне понизилась до Т2 = 290 К. Определить давление Р2 гелия, оставшегося в баллоне.
Контрольные задания 3 - 4
Вариант 5
1. Две концентрические проводящие сферы радиусами R1 = 6 см и
R2 = 10 см несут равномерно распределенные по поверхности заряды соответственно q1 = 1 нКл и q2= -0,5 нКл. Найти напряженность поля в точке, отстоящей от центра сфер на расстояние r = 15 см, используя теорему Гаусса.
2. Сила тока в проводнике равномерно увеличивается от J0 = 0 до некоторого максимального значения в течение времени t = 10 с. За это время в проводнике выделилось количество теплоты Q = 1 кДж. Найти скорость нарастания силы тока в проводнике, если его сопротивление R равно 3 Ом.
3. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению движения электрона. Скорость электрона v = 4×107 м/с. Индукция магнитного поля В = 1 мТ. Найти тангенциальное at и нормальное an ускорения электрона в поле.
4. На металл направлен пучок ультрафиолетового излучения (l = 0,25 мкм). Фототок прекращается при напряжении Uз = 1 В. Какова работа выхода А электрона из этого металла?
5. Зачерненный шарик остывает от температуры Т1 = 300 К до Т2 = 293 К. На сколько изменилась при этом длина волны lm, соответствующая максимуму спектральной плотности энергетической светимости?
Контрольные задания 1 - 2
Вариант 6
1.  Частица движется в плоскости xy по закону: x = at, y = at(1-at), где a и a - положительные постоянные, t – время. Найти уравнение траектории частицы y(x).
Частица движется в плоскости xy по закону: x = at, y = at(1-at), где a и a - положительные постоянные, t – время. Найти уравнение траектории частицы y(x).
2.  Находясь под действием постоянной силы с компонентами (3, 10, 8) Н, частица переместилась из точки 1 с координатами (1, 2, 3) м в точку 2 с координатами (3, 2, 1) м. Какая при этом совершена работа?
Находясь под действием постоянной силы с компонентами (3, 10, 8) Н, частица переместилась из точки 1 с координатами (1, 2, 3) м в точку 2 с координатами (3, 2, 1) м. Какая при этом совершена работа?
3. Столб высотой h = 3 м падает из вертикального положения на горизонтальную поверхность. Вычислить скорость V верхнего конца столба в момент его удара.
4. Частица массой m = 50 г колеблется по закону x = Acoswt, где А = 10 см и w = 5 c-1. Найти силу Fx, действующую на частицу в момент, когда фаза колебаний wt = p / 3.
5. Два моля аргона в закрытом сосуде охладили на DТ = 10 К. Найти количество отданного газом тепла.
Контрольные задания 3 - 4
Вариант 6
1. Электрическое поле образовано бесконечно длинной нитью, равномерно заряженной с линейной плотностью l = 4 нКл/м. Найти разность потенциалов двух точек поля, расположенных на расстояниях r1 = 2 см и r2 = 3 см от нити.
2. Определить заряд, протекший по проводу с сопротивлением R = 3 Ом при равномерном нарастании напряжения на концах провода от U0 = 2 В до U = 4 В в течение t = 20 c.
3. Катушка длиной l = 20 см и диаметром D = 3 см состоит из N = 400 витков. Определить индуктивность катушки.
4. При поочередном освещении поверхности некоторого металла светом с длинами волн l1 = 0,35 мкм и l2 = 0,54 мкм соответствующие максимальные скорости фотоэлектронов отличаются в 2 раза. Найти работу выхода А электронов с поверхности этого металла.
5. Вычислить энергию W, излучаемую за 1 мин c площади в 1 см2 черного тела, температура которого Т = 103 К.
Контрольные задания 1 - 2
Вариант 7
1. Частица движется со скоростью  , где a = 1 м/с2. Найти модуль скорости в момент времени t = 1c.
, где a = 1 м/с2. Найти модуль скорости в момент времени t = 1c.
2. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой m = 40 кг приложена сила F = 1кН. Определить угловое ускорение b и частоту вращения n маховика через промежуток времени t = 10 с после начала действия силы, если радиус r шкива маховика равен 12 см.
3. Человек массой М = 60 кг переходит со скоростью V’ = 1 м/с с одного конца доски-тележки на другой. Масса тележки 20 кг. Найти скорость тележки.






