Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами

1. Записываем характеристическое уравнение k² + p ⋅ k + q = 0.
2. Находим корни характеристического уравнения k₁ и k₂.
3. В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:
• , если ;
• , если ;
• , если .

2.4)

Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x) соответствуюшего однородного уравнения и частного решения y 1(x) неоднородного уравнения: Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений. Метод вариации постоянных Если общее решение y 0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение 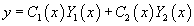удовлетворяло неоднородному уравнению с правой частью f (x). Неизвестные функции C 1(x) и C 2(x) определяются из системы двух уравнений: 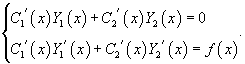Метод неопределенных коэффициентов Правая часть f (x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как   где Pn (x) и Qm (x) − многочлены степени n и m, соответственно. В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Принцип суперпозиции Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

2.5)

Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С ₁, С ₂, …, С_n определенные числовые значения.

3.1)