Лабораторные работы проводятся с помощью обучающей компьютерной системы "Теория графов". В лабораторных работах используются следующие разделы этой системы: "Основные понятия теории графов", "Экстремальные пути в графах".
Чтобы приступить к выполнению лабораторной работы необходимо запустить систему с помощью файла run.bat; выбрать в главном меню пункт "Обучающие программы"; указать раздел; выбрать пункт "Упражнения".
В процессе работы возможно обращение к теоретическому материалу, используя соответствующие пункты меню, а также алфавитный указатель.
Лабораторная работа №1. Основные понятия. Ориентированные графы
Для выполнения этой работы требуется изучить следующие понятия для ориентированного графа: определения дуги, пути, контура, односторонней и сильной связности, компоненты сильной связности, матриц смежности, инцидентности, сильной связности.
Лабораторная работа №2. Основные понятия. Неориентированные графы
Для выполнения этой работы требуется изучить следующие понятия для неориентированного графа: определения ребра, маршрута, цикла, связности, компоненты связности, матриц смежности, инцидентности, связности.
Лабораторная работа №3. Экстремальные пути в графах
Для выполнения этой работы требуется изучить определения нагруженного графа, минимального пути, максимального пути, кратчайшего пути, а также алгоритм Форда – Беллмана.
Контрольные задания по курсу "Дискретная математика".
1. Раздел «Множества»
Вариант № 1
1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В, С. Продукцию всех трех видов выпускают 10 предприятий, продукцию А и В – 18 предприятий, продукцию А и С – 15 предприятий, продукцию В и С – 21 предприятие. Число предприятий, выпускающих продукцию А равно числу предприятий, выпускающих продукцию В и равно числу предприятий, выпускающих продукцию С. Найти число всех предприятий.
2. Упростить: 
È 
È 
.
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А È В = С.
5. Эквивалентны ли множества A = { x: x 2 – 8 x + 15= 0} и B = {2, 3}?
Вариант № 2
1. В группе спортсменов 30 человек. Из них 20 занимаются плаванием, 18 – легкой атлетикой и 10 – лыжами. Плаванием и легкой атлетикой занимаются 11 человек, плаванием и лыжами – 8, легкой атлетикой и лыжами – 6 человек. Сколько спортсменов занимаются всеми тремя видами спорта?
2. Упростить: A Ç(A È B).
3. В каком случае А 
А Ç В?
4. Нарисовать диаграмму Эйлера-Венна для множества È .
5. Какое из множеств A = {1, 4, 9, 16, 25,…} и B = {1, 1/2, 1/4, 1/6, 1/8,…} имеет большую мощность?
Вариант № 3
1. В студенческой группе 20 человек. Из них 10 имеют оценку “отлично” по английскому языку, 8 - по математике, 7 - по физике, 4 - по английскому языку и по математике, 5 - по английскому языку и по физике, 4 - по математике и по физике, 3 - по английскому языку, по математике и по физике. Сколько студентов группе не имеют отличных оценок?
2. Упростить: (A \ B) È (A \ B).
3. Найти все подмножества множества A = {1, 2, 3, 4).
4
4. Пусть A n = {0, 1/2n}. Найти U A n.
n=1
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 4
1. В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной пятерки, 6 учеников получили 5 по истории, 5 – по математике и 4 – по литературе; 2 - по истории и математике, 2 - по истории и литературе, 1 - по математике и литературе. Сколько учеников получили 5 по всем предметам?
2. Упростить: (A Ç B) È (A Ç B).
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) Ç С
5. Эквивалентны ли множества A = {2 x, 0< x < ¥} и B = {2n, n = 1, 2, …}?
Вариант № 5
1. В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.
2. Упростить: (A È B) È(A È B).
3. Найти все подмножества множества A = {1, 2, 3, 4).
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 6
1. Группе студентов предложено три спецкурса: по мультимедиа, искусственному интеллекту и имитационному моделированию. 22 студента записались на спецкурс по мультимедиа, 18 – на спецкурс по искусственному интеллекту, 10 – на спецкурс по имитационному моделированию, 8 – на спецкурсы по мультимедиа и искусственному интеллекту, 15 – на спецкурсы по мультимедиа и имитационному моделированию, 7 – на спецкурсы по искусственному интеллекту и имитационному моделированию. 5 студентов записались на все три спецкурса. Сколько студентов в группе?
2. Верно или неверно равенство: (A \ B) È(A Ç B) = A?
3. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А È В = С.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È (А \ С).
5. Эквивалентны ли множества A = { x: x 2-8 x +15= 0} и B = {2, 3}?
Вариант № 7
1. Во время сессии 24 студента группы должны сдать три зачета: по физике, математике и программированию. 20 студентов сдали зачет по физике, 10 – по математике, 5 – по программированию, 7 – по физике и математике, 3 – по физике и программированию, 2 – по математике и программированию. Сколько студентов сдали все три зачета?
2. Упростить: (A È B) È (A Ç B).
3. Доказать, что множество точек A = {(x, y): y = ½ x ½, -, – 1 £ x £ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С.
5. Эквивалентны ли множества A = { y: y = x 3, 1< x <2} и B = { y: y = 3 x, 3< x < ¥}?
Вариант № 8
В группе переводчиков 15 человек владеет английским языком, 19 – французским, 8 – немецким. 9 переводчиков владеют английским и французским языком, 7 – английским и немецким, 6 – французским и немецким. 4 переводчика владеют всеми тремя языками. Сколько переводчиков в группе?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) È С?
3. В каком случае А А Ç В?
4. Нарисовать диаграмму Эйлера-Венна для множества ( È ) \ (A È B).
5. Эквивалентны ли множества A = { x: x 2 –3 x + 2 = 0} и B = {1, 3}?
Вариант № 9
1. Опрос группы студентов показал, что 70% из них любят ходить в кино, 60% в театр, 30% на концерты. В кино и театр ходят 40% студентов, в кино и на концерты – 20%, в театр и на концерты – 10%. Сколько студентов (в %) ходят в кино, театр и на концерты?
2. Верно или неверно равенство: (A Ç B) Ç (A È В) = В?
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества А \ (В Ç С).
5. Эквивалентны ли множества A = { x: x 3 – 1 = 0} и B = { x: x 2 – 3 x + 2 = 0}?
Вариант № 10
1. В группе 20 учеников. После медицинского осмотра на дополнительное обследование 14 учеников были направлены к терапевту, 6 – к окулисту, 5 – к ортопеду. К терапевту и окулисту были направлены 3 ученика, к терапевту и ортопеду –3, к окулисту и ортопеду – 2. Сколько учеников были направлены к терапевту, окулисту и ортопеду?
2. Упростить: 
( È ) \ (A È B).
3. Нарисовать диаграмму Эйлера-Венна для множества (A Ç B) È (C \ (A È B)).
4. Найти все подмножества множества A = { a, b, c, d }.
5. Эквивалентны ли множества A = {(x, y): y = ln x, 0 < x < ¥} и B = {(x, y): y = sin x, –¥ < x < ¥}?
Вариант № 11
1. При обследовании рынка спроса инспектор указал в опросном листе следующие данные. Из 1000 опрошенных 811 покупают жевательную резинку "Дирол", 752 – "Орбит", 418 – "Стиморол", 570 – "Дирол" и "Орбит", 356 – "Дирол" и "Стиморол", 348 – "Орбит" и "Стиморол", 297 – все виды жевательной резинки. Показать, что инспектор ошибся.
2. Упростить: È(B \ (A È B)).
3. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А – конечное множество, В и С – счетные множества.
4. Нарисовать диаграмму Эйлера-Венна для множества A Ç (B È C).
5. Пусть A – множество целых чисел, а B – множество четных чисел. Какие из следующих отношений справедливы: а) A = B; б) A ~ B; в) A ÉB; г) A ÊB; д) A ËB; е) A Î B.
Вариант № 12
1. Всем участникам автопробега не повезло. 12 из них увязли в песке – пришлось толкать машину, 8 понадобилась замена колеса, у шестерых перегрелся мотор, пятеро и толкали машину и меняли колесо, четверо толкали машину и остужали мотор, трое меняли колесо и остужали мотор. Одному пришлось испытать все виды неполадок. Сколько было участников?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В Ç С) = (А \ В) Ç С?
3. Доказать, что множество точек A = { y: y = 2n, n = 1, 2, …} счетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) Ç С.
5. Эквивалентны ли множества A = {(x, y): y = x 3, 1< x <2} и B = {(x, y): y = 3 x, 3< x < ¥}?
Вариант № 13
1. Из 10 участников ансамбля шестеро умеют играть на гитаре, пятеро – на ударных инструментах, пятеро – на духовых. Двумя инструментами владеют: гитарой и ударными – трое, ударными и духовыми – двое, гитарой и духовыми – четверо. Один человек играет на всех трех инструментах. Остальные участники ансамбля только поют. Сколько певцов в ансамбле?
2. Верно или неверно равенство: Ç С) = Ç С È Ç С?
3. Записать решение системы неравенств
x-2 > 0
x-5 < 0
в виде пересечения двух множеств.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç(B È C).
5. Доказать, что множества A = {(x, y): y = x 3, 1< x <2} и B = { y: y = 3 x, 3< x < ¥} эквивалентны.
Вариант № 14
1. В одной студенческой группе 10 человек могут работать на Дельфи, 10 – на Паскале, 6 – на Си. По два языка знают: 6 человек – Дельфи и Паскаль, 4 – Паскаль и Си, 3 – Дельфи и Си. Один человек знает все три языка. Сколько студентов в группе?
2. Верно или неверно соотношение: A Ç Ç C Ì A È В?
3. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А, В, и С – счетные множества.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç С).
5. Эквивалентны ли множества A = { y: y = 3 x, 0< x < ¥} и B = { y: y = 3n, n = 1, 2, …}?
Вариант № 15
1. В день авиации на аэродроме всех желающих катали на самолете, планере, дельтаплане. На самолете прокатились 30 человек, на планере – 20, на дельтаплане – 15. И на самолете, и на планере каталось 10 человек, на самолете и дельтаплане – 12, На планере и дельтаплане – 5. Два человека прокатились и на самолете, и на планере, и на дельтаплане. Сколько было желающих прокатиться?
2. Верно или неверно равенство: (A È B) \ A = B \ A?
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç С È Ç С.
5. Доказать, что множества A = { y: y = ln x, 0 < x < ¥} и B = { y: y = sin x, –¥ < x < ¥} эквивалентны.
Вариант № 16
1. Все грибники вернулись домой с полными корзинами. У десятерых из них в корзинах были белые грибы, у восемнадцати – подберезовики, у двенадцати – лисички. Белые и подберезовики были в шести корзинах, белые и лисички – в четырех, Подберезовики и лисички – в пяти. Все три вида грибов были у двух грибников. Сколько было грибников?
2. Верно или неверно равенство: (A È B) \ (A Ç B) = A Ç 
È Ç B?
3. Доказать, что множество точек A = {(x, y): y = ½ x ½, -, – 1 £ x £ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç (B È C).
5. Пусть A – множество точек отрезка [0, 1], а B – множество всех точек числовой оси. Какие из следующих отношений справедливы: а) A = B; б) A ~ B; в) A ÉB; г) A ÊB; д) A ËB; е) A Î B.
Вариант № 17
1. Все туристы взяли в поход консервы. Шесть человек взяли тушенку, пять – сгущенку, восемь – кашу (с мясом). У троих в рюкзаках была тушенка и сгущенка, у двоих – тушенка и каша, у троих – сгущенка и каша, и только в одном рюкзаке лежали все три вида консервов. Сколько было туристов?
2. Верно или неверно равенство: Ç С = С \ (С Ç (A È B))?
3. Пусть A – множество решений уравнения x 2 – 3 x + 2 = 0. Записать это множество двумя различными способами.
4. Нарисовать диаграмму Эйлера-Венна для множества (B Ç C) \ A.
5. Эквивалентны ли множества A = { x: x 2 –3 x + 2 = 0} и B = {2, 3}?
Вариант № 18
1. Было опрошено 70 человек. В результате опроса выяснили, что 45 человек знают английский язык, 29 – немецкий и 9 – оба языка. Сколько человек из опрошенных не знает ни английского, ни немецкого языков?
2. Верно или неверно равенство: (A È B) \ (A Ç B) = A Ç È Ç B?
3. Найти все подмножества множества A = { x, y, z }.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç С.
5. Счетно ли множество {(x, y): y = 3 x, 0< x < ¥}?
Вариант № 19
1. В туристической группе 10 человек знают английский язык, 10 – итальянский, 6 – испанский. По два языка знают: 6 человек – английский и итальянский, 4 – английский и испанский, 3 – итальянский и испанский. Один человек знает все три языка. Сколько туристов в группе?
2. Упростить 
.
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества С \ (С Ç (A È B)).
5. Эквивалентны ли множества A = { 2 n, n = 1, 2, …} и B = { n 2, n = 1, 2, …}?
Вариант № 20
1. Предприятие объявило набор рабочих на должности токаря, слесаря и сварщика. В отдел кадров обратились 25 человек. Из них 10 человек владели профессией токаря, 15 – слесаря, 12 – сварщика. Профессией и токаря и слесаря владели 6 человек, и токаря, и сварщика – 5 человек, и слесаря и сварщика – 3 человека. Сколько человек владеют всеми тремя профессиями?
2. Верно или неверно равенство: 
\ = \ 
?
3. Привести примеры множеств А, В и С, для которых одновременно выполняются равенства А È В È С = А и А Ç В Ç С = С.
4. Нарисовать диаграмму Эйлера-Венна для множества \ .
5. Можно ли построить взаимно-однозначное соответствие между множеством рациональных чисел отрезка [0, 1] и множеством рациональных чисел из этого интервала? Ответ обосновать.
Вариант № 21
1. Оказалось, что в группе туристов 15 человек были раньше во Франции, 19 – в Италии, 8 – в Германии. 9 туристов были во Франции и в Италии, 7 – во Франции и в Германии, 6 – и в Италии, и в Германии. 4 туриста были во всех трех странах. Сколько туристов были хотя бы в одной из трех стран?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В Ç С) = (А \ В) Ç ?
3. Привести примеры множеств А и В, для которых равенство È В =
а) выполняется; б) не выполняется.
4. Нарисовать диаграмму Эйлера-Венна для множества А Ç (В È ).
5. Найти мощность множества точек окружности с центром в точке (0, 0) и радиусом 1.
Вариант № 22
1. Группе студентов из 30 человек была предложена контрольная работа из трех задач. Первую задачу решили 15 студентов, вторую – 13, третью – 12. Первую и вторую задачи решили 7 человек, первую и третью – 6, вторую и третью – 5 человек. Все три задачи решили 2 студента. Сколько студентов из группы не решили ни одной задачи?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) Ç ?
3. Привести пример двух бесконечных множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества А Ç В Ç .
5. Найти мощность множества точек гиперболы y = 
при x Î (3, ¥).
Вариант № 23
1. Анализ историй болезней группы из 20 детей показало, что 10 детей болели ветрянкой, 6 – корью, 5 – свинкой. Ветрянкой и корью болели 3 ребенка, ветрянкой и свинкой – 3, корью и свинкой – 2. Всеми тремя болезнями болел один ребенок. Сколько детей не болели ни одной из перечисленных болезней?
2. Верно или неверно равенство: Ç С) = Ç Ç С?
3. Доказать, что множество точек A = {(x, y): y = ½ x +1½, – 1 £ x £ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (B Ç C) \ A.
5. Пусть A – множество точек отрезка [1, 2], а B – множество точек интервала (0, 3). Какие из следующих отношений справедливы: а) A = B; б) A ~ B; в) A Ì B; г) A Ê B; д) A ËB; е) A Î B.
Вариант № 24
1. В книжный киоск привезли для продажи 100 книг Пушкина, Лермонтова и Тургенева. Книги Пушкина купили 60 человек, книги Лермонтова – 50, книги Тургенева – 30 человек. Книги Пушкина и Лермонтова купили 40 человек, книги Пушкина и Тургенева – 20, книги Лермонтова и Тургенева – 10 человек. Пять человек купили книги всех трех писателей. Сколько человек не купили ни одной из перечисленных книг?
2. Верно или неверно равенство: \ = \ ?
3. Привести примеры множеств А, В и С таких, что равенство А È В È С = С
а) справедливо; б) несправедливо.
4. Нарисовать диаграмму Эйлера-Венна для множества \ .
5. Можно ли построить взаимно-однозначное соответствие между множеством натуральных чисел N и множеством действительных чисел отрезка [0, 1]? Ответ обосновать.
Вариант № 25
1. Группа научных работников состоит из 100 человек. Из них 70 человек владеют английским языком, 50 – немецким, 40 – французским, 30 – английским и немецким, 25 – английским и французским, 15 – французским и немецким. Хотя бы один язык знает каждый научный работник. Сколько человек владеют всеми тремя языками?
2. Упростить: (A \ (A Ç B)) È В.
3. Привести примеры множеств А, В и С так, чтобы A Î B, В Ì С.
4. Нарисовать диаграмму Эйлера-Венна для множества \ .
5. Можно ли утверждать, что множество всех положительных пятизначных чисел счетно? Ответ обосновать.
Вариант № 26
1. На курсы иностранных языков записалось 100 человек. Оказалось, что 70 человек будут изучать английский язык, 60 человек – французский и 30 человек - немецкий. Английский и французский собираются изучать 40 человек, английский и немецкий – 20, французский и немецкий – 10. Сколько студентов будут изучать все три языка?
2. Упростить равенство: (A Ç С)\ (С Ç (A È B)).
3. Привести пример двух различных бесконечных множеств А и В, таких, что мощность множества А равна мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç С).
5. Эквивалентны ли множества A = { x: x 3 – 1 = 0} и B = { x: x 2 – 3 x + 2 = 0}?
Вариант № 27
В команде бегунов десять спортсменов бегают на длинные дистанции, восемнадцать – на средние, двенадцать – на короткие. На длинные и средние дистанции бегают пять спортсменов, на средние и короткие – шесть. На длинные и короткие дистанции не бегает никто. Сколько бегунов в команде?
2. Верно или неверно равенство: 
È С) = È È С?
3. В каком случае A È B = А Ç В?
4. Нарисовать диаграмму Эйлера-Венна для множества È(B Ç C).
5. Можно ли утверждать, что множество всех положительных чисел имеет меньшую мощность, чем множество всех действительных чисел? Ответ обосновать.
Вариант № 28
1. В студенческой группе 25 человек. Чтобы получить допуск на экзамен по данному курсу необходимо защитить курсовую работу, выполнить лабораторную работу и сдать зачет. 15 студентов защитили курсовую работу, 20 выполнили лабораторную работу, 17 сдали зачет. Защитили курсовую работу и выполнили лабораторную работу 12 человек. Защитили курсовую работу и сдали зачет 13 человек. Выполнили лабораторную работу и сдали зачет 16 человек. Сколько студентов допущено к экзамену?
2. Упростить: Ç ( È ).
3. Привести пример двух бесконечных множеств А и В, таких, что мощность множества А меньше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества \ .
5. Эквивалентны ли множество рациональных чисел отрезка [0, 1] и множество рациональных чисел из этого интервала? Ответ обосновать.
Вариант № 29
1. В классе 20 детей. Из них 10 дополнительно занимаются в музыкальной школе, 6 – теннисом, 5 – китайским языком. Музыкальную школу и занятия по теннису посещают три ребенка, музыкой и китайским языком занимаются трое, теннисом и китайским языком двое. Всеми тремя видами дополнительных занятий занимается один ребенок. Сколько детей не занимается ни одним из перечисленных занятий?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) Ç ?
3. Доказать, что множество точек A = { y: y = 2n, n = 1, 2, …} счетно.
4. Нарисовать диаграмму Эйлера-Венна для множества A Ç È Ç B.
5. Эквивалентны ли множества A = {(x, y): y = x 2, 1< x <2} и B = {(x, y): y = 2 x, 3< x < ¥}?
Вариант № 30
1. В цеху имеется 25 станков, которые могут выполнять три вида операций: А, В и С. Из них 10 станков выполняют операцию А, 15 – В, 12 – С. Операции А и В могут быть выполнены на 6 станках, А и С – на 5, В и С – на 3 станках. Сколько станков могут выполнять все три операции?
2. Верно или неверно равенство: \ = \ ?
3. Привести примеры множеств А, В и С, для которых одновременно выполняются равенства А È В È С = А и А Ç В Ç С = С.
4. Нарисовать диаграмму Эйлера-Венна для множества Ç С.
5. Можно ли построить взаимно-однозначное соответствие между множеством действительных чисел отрезка [0, 1] и множеством действительных чисел интервала (0, 1)? Ответ обосновать.
2. Раздел «Отношения. Функции»
Вариант № 1
1. Задано бинарное отношение r = {<1, 1>, <1, 3>, <3, 1>, <3, 4>, <4, 3>}.
Найти D (r), R (r), r 
r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и транзитивного.
3. Дана функция f (x) = x 2 + ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 2
1. Задано бинарное отношение r = {<1, 3>, <3, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, но рефлексивного и транзитивного.
3. Дана функция f (x) = x 2 + e - x , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 3
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 1>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, но рефлексивного и симметричного.
3. Дана функция f (x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 4
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x 2 + y 2 = 25?
3. Дана функция f (x) = x 3 + e x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 5
1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, не рефлексивного и транзитивного.
3. Дана функция f (x) = x + e -- x , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 6
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 1>, <4, 1>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f (x) = x + e x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 7
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f (x) = x 2 +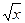 
, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 8
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f (x) = x + 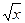, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 9
1. Задано бинарное отношение r = {<1, 2>, <2, 3>, <1, 3>, <1, 1>, <2, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и симметричного.
3. Дана функция f (x) = sinx + 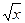, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 10
1. Задано бинарное отношение r = {<1, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = 2 y?
3. Дана функция f (x) = lnx + 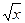, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 11
1. Задано бинарное отношение r = {<1, 1>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, инъективной, биективной.
Вариант № 12
1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x + y = 100?
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 13
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.
Вариант № 14
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f (x) = x 2 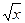, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 15
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f (x) = x 2 + 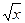, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 16
1. Задано бинарное отношение r = {< b, b >, < b, c >, < c, b >, < c, a >, < d, a >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве целых чисел..
3. Дана функция f (x) = x 2 + lnx, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 17
1. Задано бинарное отношение r = {< x, x >, < y, z >, < x, z >, < z, x >, < z, y >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного и симметричного.
3. Дана функция f (x) = x +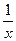 
, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 18.
1. Задано бинарное отношение r = {<1, 1>, <1, a >, < a, 1>, < a, 4>, <4, a >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного и транзитивного.
3. Дана функция f (x) = x 2 + 2 x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 19
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 3>, <3, 2>, <3, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x 2 – y 2 = 0?
3. Дана функция f (x) = 2 x + 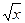, отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 20
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и не транзитивного.
3. Дана функция f (x) = x 3 ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 21
1. Задано бинарное отношение r = {<1, 3>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве треугольников на плоскости.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 22
1. Задано бинарное отношение r = {<1, 2>, <2, 2>, <2, 1>, <2, 3>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = – y?
3. Дана функция f (x) = lnx + 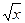, отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 23
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 3>, <3, 2>, <3, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением частичного полрядка на множестве действительных чисел отношение xry, задаваемое неравенством x 2 – y 2 £ 0?
3. Дана функция f (x) = ex + 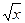, отображающая множество положительных действительных чисел на множество положительных действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 24
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <3, 2> <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество неотрицательных действительных чисел, R ® [0, ¥) и являющейся сюръективной, но не инъективной.
Вариант № 25
1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое неравенством x £ y?
3. Дана функция f (x) = lnx + 2 x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 26
1. Задано бинарное отношение r = {<2, 2>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной и неинъективной.
Вариант № 27
1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством xy = 100?
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 28
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <3, 3>, <3, 1>, <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.
Вариант № 29
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <4, 4>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка.
3. Дана функция f (x) = x 2 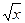, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 30
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f (x) = x 2 + 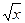, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
3. Раздел «Графы»
1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности).
2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из x 1 в x 7 в ориентированном графе, заданном матрицей весов.
3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер.
Варианты заданий
1. 1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 4 6
1 0 0 0 1 0 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 2 ¥ 10 12
0 1 0 0 1 0 ¥ ¥ ¥ ¥ 10 9 ¥ 20 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
2. 1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5
0 0 1 1 1 0 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 ¥ 1
0 0 0 0 0 0 ¥ ¥ ¥ 2 ¥ 1 ¥ ¥ 2 ¥ 1 1
1 0 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
3. 1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
4. 1.0 0 0 0 0 1 2. ¥ ¥ 5 4 2 2 9 3. ¥ 7 2 11 7
1 0 1 0 1 1 ¥ ¥ 1 1 ¥ 1 1 7 ¥ 3 ¥ 4
1 0 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 0 1 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
0 1 1 1 0 0 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
0 0 1 0 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
5. 1. 0 0 0 1 1 0 2. ¥ 4 ¥ ¥ 3 1 ¥ 3. ¥ 2 ¥ 5 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 0 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 5 ¥ 10 ¥ 13
1 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
