МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МГАПИ
УТВЕРЖДАЮ
Проректор по УР
____________ Соколов В.В.
«___» ___________ 2002 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению контрольных заданий
И лабораторных работ по дисциплине
«Дискретная математика
Рекомендуется для направления подготовки
Дипломированного специалиста
654600 – «Информатика и вычислительная техника»
специальности – 22.02.00.
Автоматизированные системы обработки
Информации и управления.
Москва 2002
АННОТАЦИЯ
Методические указания соответствуют программе курса “Дискретная математика” для студентов специальности 22.02.03. Рассматриваются следующие понятия: множества, отношения, функции, графы, булевы (переключательные) функции. Эти понятия иллюстрируются многочисленными примерами. Целью методических указаний является помощь студентам при выполнении лабораторных и контрольных работ.
Авторы: Казаков С.А., Правоторова Н.А.
Научный редактор: проф. Петров О.М.
Рецензент:____________________________________ О.М. Петров
Рассмотрено и одобрено на заседании кафедры ИТ-7
"__"____________2002 г. Зав. кафедрой __________О.М. Петров
Ответственный от кафедры за выпуск учебно-методических материалов
доц. Правоторова Н.А.
СОДЕРЖАНИЕ
Введение
Тема 1. Множества
1.1. Основные понятия
1.2. Операции над множествами
1.3. Геометрическое моделирование множеств. Диаграммы Эйлера – Венна.
1.4. Алгебра множеств. Основные тождества алгебры множеств
1.5. Эквивалентность множеств
1.6. Счетные множества
1.7. Множества мощности континуума
Контрольные вопросы к теме 1
Тема 2. Отношения. Функции.
2.1. Отношения. Основные понятия и определения
2.2. Операции над отношениями
2.3. Свойства отношений
2.4. Функции. Основные понятия и определения
Контрольные вопросы к теме 2
Тема 3. Графы.
3.1. Основные характеристики графов
3.2. Матричные способы задания графов
3.3. Изоморфизм графов
3.4. Маршруты, циклы в неориентированном графе
3.5. Пути, контуры в ориентированном графе
3.6. Связность графа
3.7. Экстремальные пути в нагруженных ориентированных графах
3.8. Алгоритм Форда – Беллмана нахождения минимального пути
3.9. Алгоритм нахождения максимального пути
3.10. Деревья. Основные определения
3.11. Минимальные остовные деревья нагруженных графов
Контрольные вопросы к теме 3
Тема 4. Булевы функции
4.1. Определение булевой функции
4.2. Формулы логики булевых функций
4.3. Равносильные преобразования формул
4.4. Двойственность. Принцип двойственности.
4.5. Булева алгебра (алгебра логики). Полные системы булевых функций
4.6. Нормальные формы
4.7. Разложение булевой функции по переменным
4.8. Минимизация формул булевых функций в классе дизъюнктивных
нормальных форм
4.9. Применение алгебры булевых функций к релейно-контактным схемам
Контрольные вопросы к теме 4
Ответы на контрольные вопросы
Указания к выполнению лабораторных работ
Вопросы к экзамену по дисциплине «Дискретная математика»
Список литературы
Краткие сведения о математиках
ТЕМА 1. МНОЖЕСТВА
Основные понятия
Определение 1.1. Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое".
Пример 1.1.
Следующие совокупности объектов являются множествами: множество деревьев в лесу, множество целых чисел, множество корней уравнения exsinx = 0.5.
Всякое множество состоит из элементов. Множества обозначают большими буквами, например А. В, С, а элементы – маленькими буквами, например, а, b, c.
Множество и его элементы обозначаются следующим образом:
А = { a 1, a 2, a 3} – множество, состоящее из трех элементов;
А = { a 1, a 2, …} – множество, состоящее из бесконечного числа элементов.
Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент a и множество, состоящее из единственного элемента a.
Пример 1.2.
Множество А = {1, 2} состоит из двух элементов 1, 2; но множество { А } состоит из одного элемента А.
Если элемент a принадлежит множеству А, это записывается следующим образом:
a Î А. Если элемент a непринадлежит множеству А, то записывают так: a Ï А.
Пример 1.3.
Пусть А 1 – множество простых чисел, А 2 – множество целых чисел, a = 4. Тогда
a Î А 2, a Ï А 1.
Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А = В.
Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В,и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А.
Если А Í В и В Í А, то по ранее введенному определению А = В.
Если А Í В и А ¹ В, то А есть собственное подмножество В, А Ì В. Если А не является собственным подмножеством В, то записывают А Ë В.
Пример 1.4.
Пусть А – множество четных чисел, В – множество целых чисел, С –множество нечетных чисел. Тогда
А Ì В, С Ì В, А Ë С, В Ë А.
Не надо смешивать отношение принадлежности (Î) и отношение включения (Í).
Пример 1.5.
Пусть А = {2} – множество, состоящее из одного элемента, В = {{2}, {4}} – множество, состоящее из двух элементов, каждое из которых является одноэлементным множеством. Тогда имеют место следующие соотношения:
2 Î {2};
{2} Ì {{2}, {4}};
2 Ï {{2}, {4}}.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. 
Принято считать, что пустое множество является подмножеством любого множества, Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.
Пример 1.6.
Множество корней уравнения sinx = 2 является пустым.
Множество всех подмножеств данного множества А называется множеством-степенью и обозначается P (A). Множество P (A) состоит из 2 n элементов (доказать самостоятельно).
Пример 1.7.
Пусть множество А = {1, 2} состоит из двух элементов 1, 2. Тогда множество P (A) включает в себя пустое множество Æ, два одноэлементных множества {1} и {2} и само множество А = {1, 2}, т. е.
P (A) = {Æ, {1}, {2}, {1, 2}}.
Мы видим, что множество P (A) состоит из четырех элементов (4 = 22).
Существуют следующие способы задания множеств.
1. Перечислением элементов множества. Например:
A = {1, 3, 5, 7, 9} – конечное множество;
B = {1, 2, …, n, …} – бесконечное множество.
2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: A = { a çуказание свойства элементов}. Здесь a является элементом множества A, a Î А. Например:
A = { a ç a – простое число} – множество простых чисел;
B = { b ç b 2 – 1 = 0, b – действительное число} – множество, состоящее из двух элементов, B = {– 1, 1};
Z = { x ç 
= 1}– множество, состоящее из одного числа, x = 0.
Операции над множествами
Рассмотрим основные операции над множествами.
Объединением множеств А и В называется множество А È В, все элементы которого являются элементами хотя бы одного из множеств А или В:
А È В = { x ç x Î А или x Î В }.
Из определения следует, что А Í А È В и В Í А È В.
Аналогично определяется объединение нескольких множеств
Пример 1.8.
а) Пусть А = {4, 5, 6}, В = {2, 4, 6}.
Тогда А È В = {2, 4, 5, 6}.
б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3:
А = {2, 4, 6, …}, В = {3, 6, 9, …}.
Тогда А È В множество чисел, которые делятся на 2 или на 3:
А È В = {2, 3, 4, 6, 8, 9, 10, …}.
Пересечением множеств А и В называется множество А Ç В, все элементы которого являются элементами обоих множеств А и В:
А Ç В = { x ç x Î А и x Î В }.
Из определения следует, что А Ç В Í А, А Ç В Í В и А Ç В Í А È В.
Аналогично определяется пересечение нескольких множеств.
Пример 1.9.
Рассмотрим данные из примера 1.8.
а) Пусть А = {4, 5, 6}, В = {2, 4, 6}.
Тогда А Ç В = {4, 6}.
б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3:
А = {2, 4, 6, …}, В = {3, 6, 9, …}.
Тогда А Ç В множество чисел, которые делятся и на 2 и на 3:
А È В = {6, 12, 18, …}.
Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество.
Пример 1.10.
Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}.
Тогда А Ç В Ç C =Æ.
Относительным дополнением множества В до множества А называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В:
А \ В = { x ç x Î А и x Ï В }.
Пример 1.11.
Рассмотрим данные из примера 1.8.
а) А = {4, 5, 6}, В = {2, 4, 6}.
А \ В = {4, 5}, В \ А = {2}.
б) А = {2, 4, 6, …}, В = {3, 6, 9, …}.
Тогда А \ В –множество чисел, которые делятся на 2, но не делятся на 3, а В \ А – множество чисел, которые делятся на 3, но не делятся на 2:
А \ В = {2, 4, 8, 10, 14, …}.
В \ А = {3, 9, 15, 21, 27, …}.
Симметрической разностью множеств А и В называется множество А + В:
А + В = (А \ В) È (В \ А).
Пример 1.12.
Рассмотрим данные из примера 1.11.
а) А = {4, 5, 6}, В = {2, 4, 6}.
А \ В = {4, 5}, В \ А = {2}, А + В = {2, 4, 5}.
б) А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}.
В \ А = {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}.
Универсальным множеством называется такое множество U, что все рассматриваемые в данной задаче множества являются его подмножествами.
Абсолютным дополнением множества А называется множество 
всех таких элементов x Î U, которые не принадлежат множеству А: = U \ A.
Пример 1.13.
Пусть А – множество положительных четных чисел.
Тогда U – множество всех натуральных чисел и - множество положительных нечетных чисел.
Геометрическое моделирование множеств. Диаграммы Венна
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис 1.1а)).
С помощью диаграмм Венна удобно иллюстрировать операции над множествами.
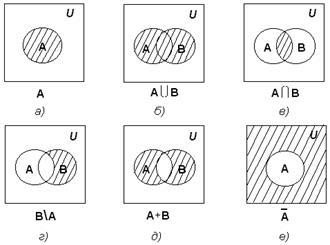
Рис.1.1
