К широкополочным сигналом относятся и сигналы с внутриимпульсной линейной частотой модуляции (ЛЧМ). Его можно представлен в виде
, (4.100)
где φ(t) – полная фаза.
Частота внутри импульса меняется по следующему закону
,
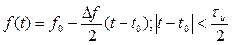где Δf – девиация частоты.
Полная фаза в момент времени t получится путем интегрирования частоты:
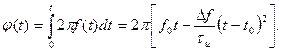
Таким образом, полная фаза сигнала изменяется по квадратичному закону. С учетом полной фазы ЛЧМ – сигнал можно записать в следующем виде
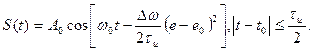(4.101)
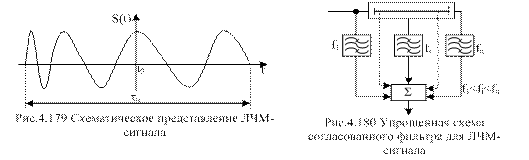
База сигнала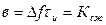 
. Внешний вид ЛЧМ – сигнала изображен на рис.4.179.
Оптимальная обработка ЛЧМ - сигнала предполагает наличие согласованного фильтра с характеристикой, зеркальной по отношению к сигналу. Из аналоговых фильтров – это дисперсионная линия задержки, у которой время задержки зависит от частоты.
Упрощенная схема согласованного фильтра для ЛЧМ – сигнала изображена на рис.4.180.
Спектр сигнала на выходе согласованного фильтра найдем по формуле
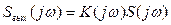
где K(jω) –передающая функция согласованного фильтра;
S(jω) – спектр внешнего ЛЧМ – сигнала.
Внешний вид спектра S(jω) изображен на рис.4.181
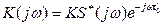
где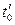 
- момент появления максимума выходного сигнала;
К – константа.
Пологая модуль спектральной плотности равным постоянной величине, получим
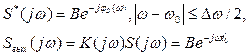
где В – амплитуда спектральных составляющих.
В соответствии с теоремой Парсеваля
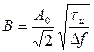, (4.102)
Сигнал на выходе согласованного фильтра во временной области найдем, используя преобразования Фурье спектральной плоскости
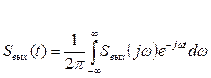
Интегрируя по положительным частотам и выделяя действующую часть получим
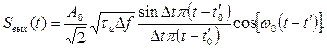(4.103)
Таким образом, выходной импульс стал в Ксж раз уже, чем входной, а его амплитуда возросла в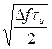 
раз.
Внешний вид импульса изображен на рис.4.172
Ширина главного лепестка по нулям равна 2/Δf, а по уровню 0,64-1/Δf. Коэффициент сжатия по этому уровню будет равен
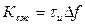
Диаграмма неопределенности ЛЧМ – сигнала изображена на рис.4.183.
При занимаемой полосе частот ЛЧМ – сигнал лучший для разрешения по времени.
Механизм сжатия сигнала в оптимальном фильтре можно пояснить следующим образом. Оптимальный фильтр осуществляет задержку спектральных компонент на время:
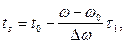(4.104)
где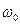 
- средняя частота;
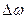- девиация частоты;
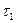- длительность импульса;
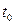- время достижения максимума сжатого импульса.
Зависимость времени задержки от частоты (4.104) изображена на рис.4.184. Время задержки является линейно убывающей функцией частоты. Зависимость времени задержки от частоты называется дисперсией.
В момент времени t мгновенная частота сигнала на входе фильтра равна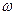 
. Колебание этой частоты поступает на выход фильтра с задержкой на 
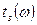, т.е. в момент 
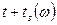. Определим этот момент:
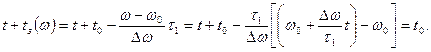
Следовательно, все спектральные составляющие сигнала (независимо от величины их частоты) задерживаются в фильтре на такое время, что поступают на его выход одновременно в момент времени 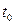. В результате арифметического сложения формируется пиковый выброс сигнала.(рис.4.185)
Форма сжатого радиоимпульса при отсутствии рассогласования по частоте определяется амплитудно-частотным спектром входного сигнала. Фазочастотный спектр, в этом случае, компенсируется фазочастотной характеристикой фильтра и не влияет на форму входного сигнала. Компенсация фазочастотного спектра сигнала является основной причиной
временного сжатия, приводя к согласованному наложению гармонических составляющих.
Обработка ФКМ – сигнала
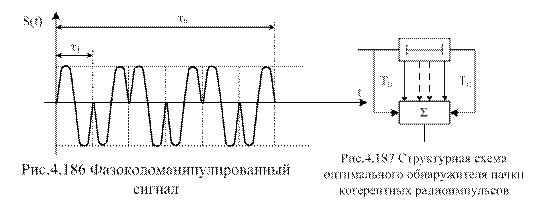
Фазокодоманипулированный сигнал – импульсный сигнал, разбитый на параллельные импульсы, у каждого из которых своя начальная фаза (рис.4.186)
Для такого сигнала имеет место соотношение
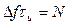
где N –количество парциальных импульсов в сигнале;
Δf – ширина спектра сигнала.
Коды фазы обычно бинарные, но могут быть и более сложные. ФКМ – сигнал может быть представлен как пачку когерентных импульсов. Для подобной пачки оптимальный обнаружитель изображен на рис.4.187
Особенности схемы следующие:
· Задержка между соседними отводами линии, задержки должны быть равны длительности парциального импульса τ1;
· В некоторые отводы линии задержки должны быть включены фазовращатели, обеспечивающие синфазное суммирование сигналов.
Структурная схема оптимального обнаружителя ФКМ – сигнала изображена на рис.4.188
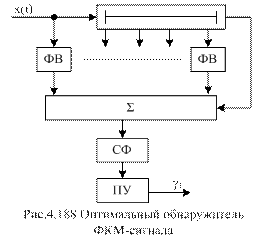
На схеме обозначены: ФВ – фазовращатели; СФ – согласованный фильтр. На рис.4.189 и 4.190 изображены схемы оптимального обнаружителя и эпюры напряжений для сигнала, состоящего из трех парциальных импульсов.
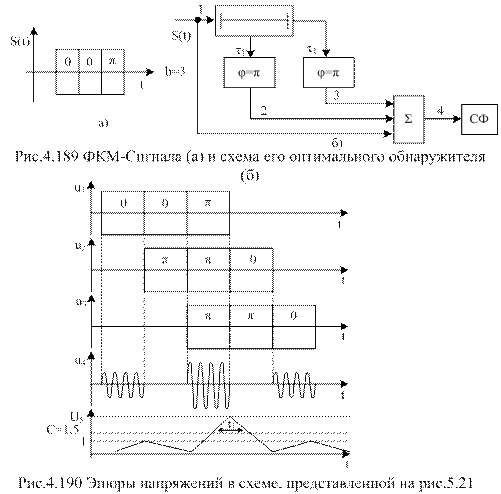
Одним из основных параметров, характеризующих радиолокационную систему является коэффициент различимости, который определяется как отношение минимальной мощности сигнала на входе приемника Pмин к мощности шума
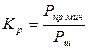
Характеристики обнаружения зависят от энергии сигнала
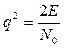
где E=NE1 (N – количество импульсов в пачке; Е1 – энергия
одиночного импульса)
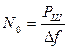
Подстановка дает следующий результат
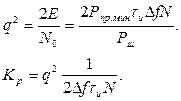(4.105)
Таким образом отношение сигнал/шум по мощности на выходе приемного устройства Кр может быть малым (в частности и меньше единицы) если производится оптимальная обработка достаточно длинной пачки радиоимпульсов либо одиночного радиоимпульса с достаточно большой базой.
