В качестве сложного сигнала возьмем сначала ЛЧМ импульс. Оптимальный фильтр для такого сигнала состоит из полосового фильтра ПФ и дисперсионной линии задержки ДЛЗ, которая фактически выполняет функции фазового компенсатора ФК. Пусть этот фильтр располагается после ограничителя, которому предшествует лишь широкополосный фильтр (рис.4.155,а).
Поскольку полосовой фильтр можно рассматривать в качестве узкополосного, то схема до фазового компенсатора представляет собой схему ШОУ с шириной полосы «узкополосного» фильтра DFy = Df, где Df —девиация частоты ЛЧМ сигнала. Поэтому на ее выходе, т. е. на входе фазового компенсатора, отношение сигнал-шум составляет 
, а отношение помеха-шум
(4.75)
Амплитуда ЛЧМ сигнала увеличивается в ДУЛЗ фазовом компенсаторе в 
раз, а мощность шума не претерпевает изменений. Поэтому на выходе фазового компенсатора отношение сигнал-шум составляет 
. При длительности помехи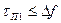 
меньшей длительности сжатого в ДЛЗ ЛЧМ
импульса, длительность ее на выходе полосового фильтра равна 1/Df. На выходе ДЛЗ помеха в этом случае расширяется до длительности ЛЧМ импульса t1, а ее амплитуда уменьшается в 
раз. Поэтому
При длительности помехи, меньшей длительности переходного процесса в ДЛЗ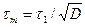 
, помеха расширяется в ДЛЗ до 
и амплитуда ее на
выходе уменьшается в 
раз. В этом случае (при 
) отношение помеха-шум составляет
При tП1 > tm помеха проходит через ДЛЗ, не изменяя своей длительности и амплитуды. Поэтому отношение помеха-шум на выходе ДЛЗ совпадает с этим отношением на выходе полосового фильтра, которое равно 
.
Следовательно, отношение помеха-шум на выходе
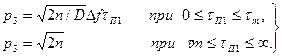
Поскольку n >1, отношение помеха-шум будет меньше единицы, если ее длительность удовлетворяет условию
(4.76)
Это условие нормирования помехи к уровню шума.
Далее пусть сложным сигналом является рассмотренный ФМ сигнал общей длительности t1 составленный из радиоимпульсов длительностью t0 = t1/N,
которые различаются временным положением и могут различаться начальной фазой 
. Последняя принимает одно из двух значении: 0 и p. Тогда полосовой фильтр ПФ на схеме (см. рис.4.154) который будем считать «узкополосным», представляет собой оптимальный 
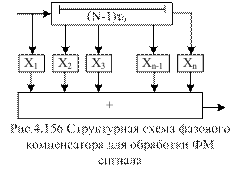
фильтр для радиоимпульса длительностью t0, а фазовый компенсатор ФК — совокупность линии задержки на время (N—1) t0 с (N—2)-мя равномерно расположенными отводами, N фазовращателей на угол 
сумматора (рис.4.156).
Тогда на входе фазового компенсатора, как на выходе схемы ШОУ,
отношение сигнал-шум составит , а отношение помеха-шум
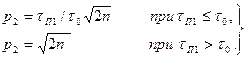, (4.77)
где в данном случае n = DFшt0.
Шум после прохождения полосового фильтра, являющегося оптимальным фильтром для радиоимпульса длительностью t0, будет иметь треугольную АКФ с шириной основания 2т0. Поэтому шумы на входах сумматора не коррелированы и суммируются в нем по мощности, ввиду чего 
. Поскольку сигнал возрастает в фазовом компенсаторе в N раз по амплитуде и в N2 раз по мощности, то отношение сигнал-шум на его выходе составит
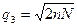. (4.78)
Помеха малой длительности (tП1< t0) растягивается полосовым фильтром до длительности t0 элементарного импульса, а если длительность помехи превышает указанное значение, то фильтр оставит ее без изменения.
Поэтому при тП1 < t0 помехи на входах сумматора могут накладываются друг на друга только фронтами, что не приведет к увеличению амплитуды помехи на выходе. Вследствие этого и того, что мощность шумов возрастает, отношение помеха-шум на выходе фазового компенсатора уменьшится в 
раз:
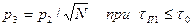
Если длительность помехи не менее длительности сигнала (tП1 > t1 = Nt0), то помехи на входах сумматора будут перекрываться, вследствие чего амплитуда помехи на выходе будет больше в раз, чем на входе. Суммирование помех по мощности, а не по напряжению объясняется квазислучайным законом изменения коэффициентов передачи фазовращателей, который обусловлен псевдослучайным характером используемого кода. Вследствие того, что в данном случае и помеха, и шум возрастают в одинаковой степени, их отношения не меняются:
По-видимому, в промежуточном случае 
имеем
Отношение помеха-шум на выходе
. (4.79)
Поскольку при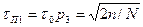 
, то отношение помеха-шум не больше единицы, если длительность этой помехи удовлетворяет условию
Это условие нормирования помех к уровню шума. Оно выполняется только для достаточно коротких помех.
Таким образом, рассматриваемая система обработки (см. рис. 6.94,а) с оптимальной фильтрацией после ограничения нормирует к уровню шума только достаточно короткие импульсные помехи. В этом и заключается ее существенный недостаток, который объясняется тем, что помехи, ограниченные до уровня шума в ограничителе, накапливаются в узкополосном полосовом фильтре. Поэтому устранить указанный недостаток можно только путем ликвидации этого накопления (интегрирования) помех.
Поскольку совсем убрать полосовой фильтр ПФ невозможно, ибо он осуществляет абсолютно необходимую оптимальную частотную фильтрацию сигналов от шумов, то поставим его перед ограничителем (см. рис. 6.94, б). При таком построении схемы необходимость в применении широкополосного фильтра отпадает. Указанный полосовой фильтр осуществляет первую основную операцию оптимальной фильтрации — частотную фильтрацию. Вторая операция — компенсация фазовых сдвигов между спектральными составляющими сигнала — производится фазовым компенсатором. Полоса пропускания последнего может быть неограниченно большой. Поэтому накопление помех (и сигналов) в нем можно полностью устранить, ввиду чего его вполне можно поставить после ограничителя.
Рассмотрим действие сигнала, помех и шумов на систему, в которой полосовой фильтр предшествует ограничителю, а фазовый компенсатор стоит после него (см. рис. 6.94,6).
Так как уровни сигнала, шума и помехи на выходе ограничителя одинаковы, то отношение сигнал-шум и отношение помеха-шум составляют
В случае ЛЧМ сигнала его амплитуда увеличивается фазовым компенсатором в раз, а уровень шума остается неизменным. Поэтому отношение сигнал-шум на выходе 
. В случае ФМ сигнала его амплитуда возрастает в фазовом компенсаторе в раз, а среднеквадратическое значение шума — в N раз, ввиду чего отношение сигнал-шум на выходе 
.
Как следует из предыдущего, фазовый компенсатор может только оставить без изменения или даже уменьшить отношение помеха-шум 
.
Следовательно, система обработки сложного сигнала, состоящая из узкополосного полосового фильтра, ограничителя и широкополосного фазового компенсатора, позволяет нормировать к уровню шума импульсные помехи любой длительности. В этом и заключается ее несомненное достоинство. Она реализует одно из основных преимуществ системы со сложными сигналами — ее помехозащищенность, обусловленную сложной фазовой структурой этих сигналов.
