Характеристики сигналов РЛС
Сигналы используемые в РЛС определяют степень разрешения по различным параметрам (координатам).
Относительно потенциальной разрешающей способности по дальности следует сказать следующее, рассматривая случай двух узкополосных сигналов S(t) и S(t-τ).
В соответствии с положением введенным Ф.М. Вудвортом, сигналы S(t) и S(t-τ) разрешаются, если мера различия между ними ε2 достаточно велика.
, (4.91)
где Е – энергия сигнала на нагрузке в 1 Ом.
При этом сигнале S(t) представлен в следующей форме
где 
- комплексная амплитуда сигнала.
Если сигналы узкополосные, член 
осциллирует быстрее, чем изменяется функция 
По этой причине учитывать его при оценке разрешающей способности нецелесообразно. Тогда
, (4.92)
где 
Функция 
получила название функции неопределенности по дальности. Ее значение при различных временных сдвигах сигналов τ определяет меру различимости между ними.
Какова должна быть минимальная разница между сигналами ε2, чтобы они различались? Следуя Вудворду, потенциальная разрешающая способность 
определяется как основание прямоугольника высотой 
, равновеликого площади под кривой 
(рис.4.165):
Используя преобразование Фурье
, (4.93)
где 
- эффективная ширина спектра сигнала. Таким образом, потенциальная разрешающая способность по времени (а следовательно, и по дальности) обратно пропорциональна эффективной ширине спектра сигнала.
На практике алгоритм разрешения реализуется согласованными фильтрами (рис.4.166)
При движении цели относительно РЛС принимаемые сигналы имеют Доплеровское смещение частоты.
В этом случае
,
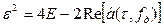где 
- функция неопределенности по дальности и радиальной скорости.
В общем случае - сложная функция двух аргументов.
Пологая в частном случае fд=0 получим
В другом частном случае τ=0, получаем
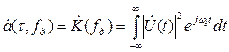
Функция 
носит название функции неопределенности по частоте (по скорости).
Потенциальная размещающая способность по частоте определяется следующим образом
На рис.4.167. изображен квадрат модуля функции неопределенности по скорости
, (4.94)
где τэ – эффективная длительность сигнала.
Функцию 
можно представить как поверхность в трехмерном пространстве, которая называется поверхностью неопределенности, а ограниченная ее фигура – телом неопределенности (рис.4.168)
Потенциальная совместная разрешающая способность по времени и частоте находится как площадь основания цилиндра, имеющего такой же объем и такую же высоту, что и тело неопределенности
Фактически 
представляет собой площадь области высокой корреляции (рис.4.169).
