Одноканальное измерение угловой координаты

 

Системы измерения угловых координат q(q = b или q=e), иначе системы пеленгации, могут содержать один или несколько приемных каналов. Соответственно этому методы пеленгации де­лятся на одноканальные и многоканальные.

Одноканальные методы пеленгации основаны на использовании зависимости амплитуды принятого сигнала от разности углов (q_М —q_Ц) между направлением максимума результирующей диаграммы и направлением прихода отраженных сигналов.

Пусть обзор по угловой координате q производится с постоянной скоростью W_А, так что положение максимума результирующей ди­аграммы q_М = W_Аt. При этом амплитуда отраженного сигнала на входе приемника

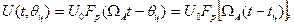(3.4)

где t_ц = q_ц/W_А — момент пересечения максимумом диаграммы на­правления на цель.

В случае импульсного излучения на входе приемника образует­ся пачка радиоимпульсов с огибающей (3.4).

Вначале рассмотрим обработку нефлюктуирующей пачки импульсов со случайными начальными фазами. Полагая угловую коор­динату цели равной q_Ц = W_Аt_ц ло­гарифм отношения правдоподобия представим в виде

 

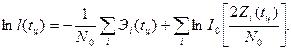(3.5)

В приведенном выражении Э_i(t_ц) и Z_i(t_ц) — энергия и модуль корреляционного интеграла для i-го импульса пачки, время запаз­дывания огибающей которой равно t_ц. Пусть форма импульсов сигнала описывается функцией U(t). Поскольку огибающая форми­руется в соответствии с результирующей диаграммой направлен­ности 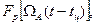, выражение для комплексной амплитуды i-го радиоимпульса может быть представлено в виде

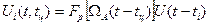, (3.6)

где t_i — момент прихода i-го импульса.

Считая, что импульсы имеют малую длительность и форма их огибающей не искажается из-за перемещения диаграммы направлен­ности за время этой длительности, заменим в (3.6) разность (t — t_ц) на (t_i — t_ц). Тогда получим

.

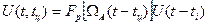Величины Э_i (t_ц) и Z_i (t_ц) в выражении (3.5) можно при этом представить в виде

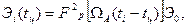(3.7)

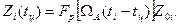
Здесь Э₀ —энергия одного радиоимпульса, рассчитанная для слу­чая, когда цель расположена на оси диаграммы направленности ан­тенны; Z_0i — модуль корреляционного интеграла, который выра­батывается без учета модуляции диаграммой направленности антенны,

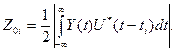
Оптимальная оценка времени запаздывания пачки 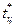определяется из условия

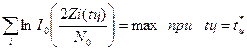, (3.8)

где N₀ – спектральная плотность шума;

I₀- модифицированная функция Бесселя первого рода нулевого порядка.

Позволяя синтезировать схему обработки, условие (3.8) приводит, однако, к слишком сложному ее виду. Схема упрощается, если амплитуды импульсов достаточно большие или малые .

Рассмотрим вначале первый случай 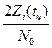>>1 случай силь­ного сигнала. Пользуясь линейным асимптотическим представле­нием ln I₀ (и) 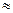u при и >> 1, условие оптимальности оценки в со­ответствии с выражением (3.8) приведем к виду

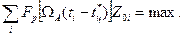(3.9)

Выражение (3.9) соответствует проведению оптимальной обработ­ки в два этапа. На первом этапе (рис. 3.13) радиоимпульсы пачки усиливаются линейной частью оптимального для них приемника. В результате детектирования получаются видеоимпульсы с ампли­тудами Z_0i. На втором этапе вводятся весовые коэффициенты Si= 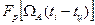. В зависимости от предполагаемых оценок ве­личины t_ц составляются весовые суммы и устанавливается такое 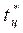, для которого сумма максимальна.

 

По способу образования весовых сумм последетекторная обработ­ка может быть корреляционной или фильтровой. При корреляционной обработке приемник стробируется по дальности (рис. 3.13) для вы­деления сигналов от интересующей цели и исключения шумов между радиоимпульсами. Снимаемая с выхода детектора стробированная пачка видеоимпульсов с амплитудами Z_0i подается на параллельные каналы, рассчитанные на различные значения t_ц. В каждом канале значения Z_0i

(i = 1,2,..., М) умножаются на соответствующие коэф­фициенты S_i = F_p[W_A(t_i—t_ц)] и результаты суммируются. В ка­честве оценки времени запаздывания пачки t_ц принимается значе­ние t_ц канала, для которого весовая сумма максимальна. Сущест­венным недостатком корреляционной схемы является ее многоканальность.

Фильтровая схема в отличие от корреляционной позволяет ве­сти одноканальную обработку пачек видеоимпульсов

Видеоимпульсы с выхода приемника запоминаются с последующим воспроизведением. Воспроизводимые сигналы усиливаются, а затем суммируются. Число усилителей должно соответствовать числу импульсов в пачке М. Значения коэффициента усиления к₁,к₂…к_м весовых усилителей выбираются в соответствии с результирующей диаграммой направленности антенны. Максимальная амплитуда выходного сигнала получается в момент времени 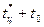, где t₀- время запаздывания максимума огибающей пачки в схеме обработки. Рассмотренный метод обработки называют методом симметричных весовых коэффициентов.

 

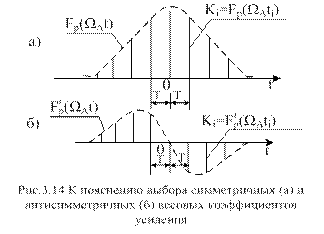
Учитывая, что производная гладкой функции в точке максимума равна нулю, видоизменим условие (3.9) оптимума оценки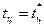

,

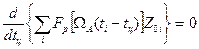или

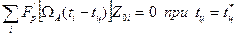. (3.10)

Весовая сумма (3.10) реализуется рассмотренными схемами корре­ляционной или фильтровой обработки, если четную функцию веса заменить нечетной

(рис. 3.14, б). Оценка времени запаздывания пачки 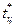определяется при этом из условия минимума суммы (3.10). Рассмотренный метод обработки называется методом антисимметричных весовых коэффициентов.

При слабом сигнале квадратичный детектор теоретически более предпочтителен, чем линейный. Оптимальная функция веса при этом соответствует квадрату результирующей диаграммы направленности при методе симметричных или производной квадрата при методе антисимметричных весовых коэффициентов. Однако разница в эффективности обработки с квадратичным и линейным детектором, мала.

Большинство результатов распространяется на пачку импульсов с независимыми случайными амплитудами и начальными фазами.

Таким образом, во всех основных случаях оптимальной является обработка по методу симметричных или антисимметричных весовых коэффициентов.

Ввиду сложности долговременного запоминания многие практические методы определения положения центра пачки основаны на кратковременном запоминании с использованием основных идей весовой обработки.

В основе практических методов определения углового положения центра пачки лежит использование квазиоптимальных весовых функций и сокращение объема памяти при незначительном возрастании погрешностей измерения. Могут использоваться как симметричные, так и антисимметричные квазиоптимальные весовые функции (рис. 3.15). К числу основных методов определения центра пачки при этом относят методы интегрирования импульсов, сравнения площадей, счета импульсов, а также методы «вилки», максимума и минимума.

Методы интегрирования импульсов основаны на использовании симметричной прямоугольной весовой функции (рис. 3.15, а), которая близка к оптимальной при независимых флюктуациях амплитуд импульсов пачки и большом отношении сигнала к шуму. Оценка времени запаздывания t*_ц в этом случае определяется из условия . С учетом

 

запаздывания в системе обработки она соответствует моменту максимума напряжения на выходе сумматора. При одинаковых длительностях весовой функции и пачки это напряжение пропорционально сумме всех ее импульсов. Если длительность весовой функции меньше длительности пачки, суммируется только часть импульсов.

Методы сравнения площадей основаны на применении антисим­метричных весовых функций (рис. 3.15, е, ж). Использование весовой функции (рис. 3.15, е) заключается в следующем. Видеоимпульсы от выбранной цели подаются на схему сравнения площадей, содержащую в данном случае только два весовых усилителя, один из которых является инвертором. Площадь видеоимпульсов (рис. 3.16, а) в момент оптимального отсчета разбивается на две равновеликие части.

Отсчет угловой координаты цели производится в момент времени, когда напряжение на выходе сумматора равно нулю с учетом запаздывания в схеме обработки. Обработка пачки импульсов при весовой функции, изображенной на

рис. 3.15, ж, отличается от рассмотренной тем, что площади части импульсов не суммируются (рис. 3.16,. б).

При сравнении площадей возможно образование зоны нечувст­вительности. Поэтому от разбиения площади видеоимпульсов переходят к разбиению площади под огибающей пачки (рис. 3.16, в). Для этого видеоимпульсы выбранной цели сначала подают на схему выделения огибающей и только после этого на схему сравнения площадей, например, временной дискриминатор.

 

 

Определение угловой координаты по центру отметки на экране индикатора также может быть отнесено к сравнению площадей. Накопление яркостей в отдельных точках экрана соответствует при этом первой ступени интегрирования. Основное интегрирование — по промежуткам времени, составляющим половину длительности пачки, производится оператором визуально — при определении центра дужки.

Методы счета импульсов, превышающих порог, также сводятся к интегрированию импульсов, но аналоговое суммирование заменяется цифровым. Для измерения положения оси антенны не обязательно запоминать момент прихода каждого импульса пачки. Могут запоминаться только моменты ее начала и конца.

Запоминающее устройство при этом существенно упрощается. Счет числа импульсов, превышающих порог, ведется на временном интервале, составляющем часть общей длительности пачки. Угловая координата цели определяется как среднее арифметическое значений координат оси антенны, соответствующих началу и концу пачки. Для ослабления влияния ложных импульсов и пропусков сигнала на точность измерения начало и конец пачки определяются по специальному критерию (логике). В качестве критерия может быть выбран, в частности, следующий. Если за три последовательных периода повторения обнаружен один импульс, он считается ложным (рис. 3.17), если два — они считаются началом пачки.

 

 

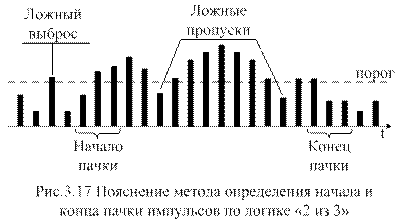
Конец пачки отмечается, если в трех последовательных периодах после начала когда впервые обнаружен пропуск двух импульсов (пропуск только од­ного импульса считается ложным).

В общем случае может использоваться логика «п из m». Логики могут быть целыми (п = т) и дробными (п <m). Для определения начала и конца пачки могут использоваться одинаковые логики, либо различные. При использовании различных логик менее жест­кая определяет конец пачки, чтобы исключить ее дробление вслед­ствие флюктуационного выпадения отдельных импульсов. Пусть для определения начала пачки используется логика «3 из 3» (3/3). Тогда дробление пачки менее вероятно, когда ее конец определяется логикой «2 из 3» (2/3) или какой-либо другой менее жесткой логи­кой. Ею может быть логика «3 из 3» с дополнительным условием, чтобы в конце пачки следовало два нуля подряд (логика 3/3-00).

Методы вилки, максимума и минимума являются исторически одними из первых методов измерения угловых координат. Метод вилки состоит в oопределении координаты по двум засечкам q₁ и q₂, соответствующим одинаковым значениям амплитуды сигнала при отвороте антенны в ту и другую сторону от направления на цель. Искомая координата находится как среднее арифметическое q*=(q₁+q₂)/2. Метод вилки эквивалентен использованию антисимметричной весовой функции (рис.3.15, д).

При методах максимума и минимума используется, по существу, весовая функция, изображенная на рис. 3.15, г (метод максимума) или противоположная ей по знаку (метод минимума). Диаграмма направленности антенны радиолокатора при методе минимума выбирается с резко выраженным провалом (рис. 3.18).

 

 

Оценка угловой координаты цели производится по положению антенны, соответствующему максимуму или минимуму сигнала. В первых ра­диолокаторах, поворачивая антенную систему, оператор следил за изменением амплитуды сигнала по экрану индикатора. Когда амплитуда оказывалась максимальной или минимальной, производился отсчет по шкале, связанной с поворотным механизмом антенны. Недостатком метода максимума является его малая точность вследствие слабого изменения амплитуды сигнала в окрестности максимума. При остром провале в диаграмме направленности метод минимума обеспечивает более высокую точность, чем метод максимума, однако его возможности снижаются из-за низкого уровня сигнала в рабочей точке. Поэтому область использования методов максимума и минимума сужается.

 

Методы радиопеленгации

 

Измерение угловых координат основано на определении угла прихода радиоволн, излученных или отраженных объектом. Для этого используют радиопеленгаторы. Важной характеристикой радиопеленгатора является его пеленгационная характеристика u(a) –зависимость нормированного выходного напряжения приемника от направления прихода радиоволн. В зависимости от того, какой параметр радиосигнала оказывает основное влияние на формирование пеленгационной характеристики, методы углометрии (пеленгации) подразделяют на амплитудные, фазовые, частотные и комбинированные (амплитудно-фазовые). Основными из этих методов, нашедшими распространение на практике, являются первые два.

Амплитудные методы. Амплитудные методы пеленгации основаны на использовании направленных свойств антенн. Если используются направленные свойства только приемной антенны, ДН которой равна f_пр(a), то пеленгационная характеристика радиопеленгатора u(a)=к×f_пр(a), где к – коэффициент пропорциональности.

При использовании направленных свойств как приемной, так и передающей антенны u(a)=к·f_пр(a)· f_пер(a), где f_пер(a) – ДН передающей антенны. Если на передачу и прием работает одна антенна, то f_пер(a) = f_пр(a) = f(a), при этом u(a)=к·f ²(a).

Среди амплитудных методов пеленгации различают методы максимума, минимума и сравнения. Пеленгация методом максимума (рис. 3.19, а) осуществляется путем совмещения направления максимума пеленгационной характеристики a с направлением на пеленгуемый объект a₀ в результате плавного вращения ДН антенны; пеленг отсчитывается в тот момент, когда напряжение на выходе приемника становится максимальным. Достоинства метода максимума: простота технической реализации, получение наибольшего отношения сигнал-шум в момент отсчета пеленга. Недостатки метода: низкая пеленгационная чувствительность и, как следствие, низкая точность пеленгации.

 

 

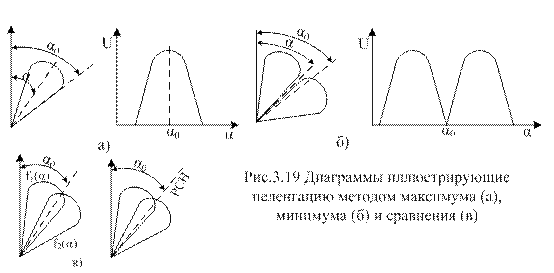
Пеленгационная чувствительность – это способность радиопеленгатора измерять напряжение на выходе приемника при изменении положения ДН антенны относительно направления на объект. Чем больше изменение напряжения при заданном изменении угла, тем выше пеленгационная чувствительность. Количественной мерой пеленгационной чувствительности является крутизна пеленгационной характеристики

.

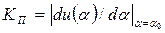Если Δu – минимальное изменение выходного напряжения приемника, которое может зафиксировать измеритель, то абсолютная погрешность измерения угловой координаты Δa ≈ Δu/K_П. Таким образом, чем больше крутизна пеленгационной характеристики, тем выше пеленгационная чувствительность и тем меньше погрешность измерения угла.

Так как максимум ДН антенны обычно «тупой», то пеленгационная чувствительность при пеленгации методом максимума мала и, следовательно, погрешность измерения невысока.

Пеленгация методом минимума (рис. 3.19, б) осуществляется путем плавного вращения ДН с резким провалом. Угол отсчитывается в тот момент, когда направление минимума пеленгационной характеристики a совпадает с направлением на объект a₀, при этом напряжение на выходе приемника минимально. Крутизна пеленгационной характеристики в этом случае выше, чем при методе максимума, поэтому выше и точность пеленгации. Однако амплитуда принимаемого сигнала вблизи направления на объект мала и, следовательно, использование метода минимума в активной радиолокации нецелесообразно. Этот метод применяется главным образом в радионавигации при пеленгации источников мощного собственного излучения.

При пеленгации методом сравнения (рис. 3.19, в) угол определяется по соотношению амплитуд двух принимаемых сигналов, соответствующих двум пересекающимся диаграммам направленности f₁(a) и f₂(a). Приемник в этом случае двухканальный, причем напряжения на выходе каналов пропорциональны значениям f₁(a₀) и f₂(a₀):

.

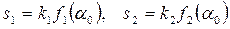Сравнивая эти сигналы, например путем деления, находим

.

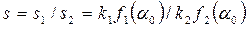Измерив отношение s и решив уравнение относительно a₀, найдем искомый угол. Достоинством метода сравнения является возможность быстрого определения направления на объект (в течение одного импульса) в пределах сравнительно широкого сектора при неподвижных антеннах. Однако точность измерения может иногда оказаться низкой в зависимости от вида и взаимного положения ДН антенн и угла прихода радиоволн.

В том случае, когда отношение сигналов s₁/s₂ стремятся сделать равным единице, приходим к равносигнальному методу пеленгации. При этом методе ДН антенной системы поворачивается до тех пор, пока объект не окажется на равносигнальном направлении РСН (см. правый рис. 3.19, в), когда s = s₁/s₂ = 1. Достоинство равносигнального метода – сравнительно высокая точность пеленгации, так как при измерении используется та часть ДН, которая обладает большой крутизной. Данный метод применяется при автоматическом слежении по угловым координатам за движущимся объектом. В этом случае удобнее формировать не отношение сигналов, а их разность s = s₁–s₂. Система управления поворачивает антенну (или ДН при неподвижной антенне) в ту или иную сторону (в зависимости от знака величины s), стремясь свести рассогласование s к нулю. При этом равносигнальное направление будет отслеживать изменение направления на объект. В системах посадки равносигнальные направления задают направления курса и глиссады.

Методы сравнения, в частности равносигнальный, используют в многоканальных (моноимпульсных) радиопеленгаторах и в одноканальных. В первом случае благодаря многоканальности приемной системы сравнение сигналов происходит в один и тот же момент времени. Во втором случае нужно периодически менять положение ДН антенны в пространстве, при этом сравниваются между собой сигналы, принятые в разные моменты времени при различных положениях ДН. Одноканальные радиопеленгаторы проще многоканальных, однако менее помехозащищены и обеспечивают меньшую точность.

Фазовый метод. Фазовый метод пеленгации основан на измерении разности фаз электромагнитных колебаний, принятых на две разнесенные антенны. Пусть в точках А и В, расстояние между которыми d (рис. 3.20), расположены приемные антенны. Разность фаз принимаемых колебаний φ_р = (2π/λ)(R_A – R_B), где R_A, R_B — расстояния от антенн до объекта. При R_A >> d, R_B >> d имеем

, (3.11)

где a – угол между нормалью к базе и направлением на объект.

Измерив разность фаз φ_р, найдем

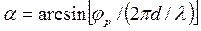. (3.12)

При пеленгации объекта не на плоскости, а в пространстве, когда требуется определять две угловые координаты, нужна вторая пара антенн, база которых пересекается с базой первой пары.

В качестве фазочувствительного элемента можно использовать фазовый детектор. Напряжение на его выходе пропорционально косинусу разности фаз:

s = к· cos φ_р. Пеленгационная характеристика u(a) = cos[(2π/λ)d sina].

При малых углах sina ≈ a, поэтому u(a) = cos[(2π/λ)da] (1 на рис. 3.21). Так как в окрестности a = 0 крутизна пеленгационной характеристики мала, то и точность пеленгации будет низкой. Кроме того, поскольку рассматриваемая пеленгационная характеристика является четной функцией угла, то его определение будет двузначным, т.е. нельзя будет определить

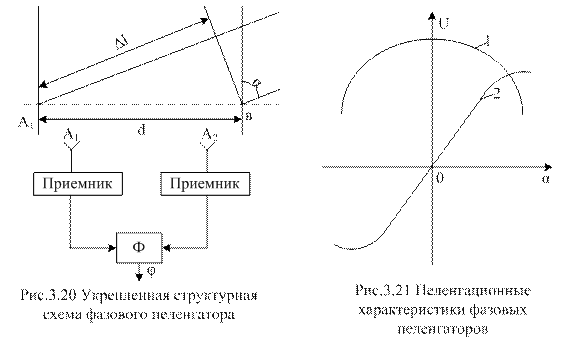
направление смещения объекта от перпендикуляра к базе.

Эти недостатки устраняются, если ввести в один из приемных каналов после резонансного усилителя РУ фазовращатель ФВ на π/2 (рис. 3.22). Напряжение на выходе фазового детектора ФД измеряется вольтметром В. Благодаря смещению фазы сигнала в одном из каналов на π/2 пеленгационная характеристика становится нечетной функцией (2 на рис. 3.21)

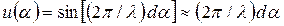, (3.13)

при этом ее крутизна K_П = 2πd/λ. Как видим, пеленгационная чувствительность, следовательно, точность пеленгации растет с увеличением отношения d/λ. Однако при этом будет уменьшаться диапазон однозначного измерения угла Δa_max. Действительно, поскольку для однозначного измерения разности фаз с помощью фазового детектора необходимо, чтобы φ ≤ π, а при малых a согласно φ_р ≈ 2πda/λ, то Δa_max = λ/2d.

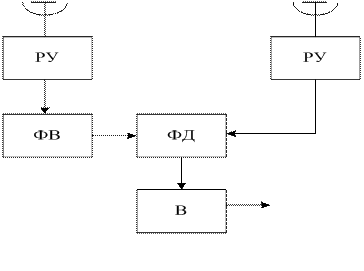
Рис.3.22 Структурная схема фазового пеленгатора

 

Для обеспечения высокой точности и в то же время однозначности измерений можно применить многошкальный метод (подобно фазовой дальнометрии). При двухшкальном методе вводят третью антенну и создают большую и малую базы. Пара антенн с малой базой обеспечивает грубое, но однозначное измерение угла (в диапазоне Δa_max). Антенны с большой базой дают более точный отсчет.

Неоднозначность пеленгации можно устранить также, применив антенны с достаточно узкими ДН: их ширина a_а не должна превышать диапазон однозначной пеленгации, т.е. a_а ≤ Δa_max. Кроме того, остронаправленные антенны обеспечивают разрешение объектов по угловым координатам.