Задача 1. РРрРРассмотрим отображение f: 
. Выяснить, какие из приведенных ниже отображений являются инъективными, сюръективными: 1) f(x)=x4; 2) f(x)=3-x; 3) f(x)=x2-x3; 4) f(x)=x+x3; 5) f(x)=|x|; 6) f(x)=x3+6; 7) x+|x|.
Задача 2. На множестве людей L рассмотрим отображение f: L®L, сопоставляющее каждому человеку его мать. Является ли оно инъективным? Сюръективным?
Задача 3. На множестве точек плоскости рассмотрим отображение симметрии точки относительно начала координат. Будет ли оно инъективным? Сюръективным?
Задача 4. На множестве точек плоскости рассмотрим отображение проектирования точки на ось Ох. Является ли оно инъективным?
Мощность множества
Мощностью конечного множества А называется количество элементов в нем. Мощность принято обозначать card A.
Декартовым произведением множеств А и В называется множество АхВ, состоящее из всех упорядоченных пар {(а, b), а ÎА, b ÎВ}.
Правило произведения: для любых конечных множеств А и В card AxB=cardA×card B.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Заданы множества А{1,2}, В={3,4}. Выписать все элементы множества АхВ.
Решение. АхВ={(1,3),(1,4),(2,3),(2,4)}.
Задача 2. Верно ли, что мощность разности двух множеств равна разности их мощностей? В каких случаях это верно?
Решение. Рассмотрим множества А и В. card (A\B)=cardA\cardB верно в следующих случаях:
1. Если В=Æ, например, А={ a,b,c }, B=Æ. По определению А\В={ a,b,c }, card A=3, card B=0, card (A\B)=3. Итак, card (A\B)= card A - card В.
2. Если А£В, А={ a,b,c }, B={ a,b }, А\B={ с }Þ card (A\B)=1, card A - card B=3-2=1.
Итак, card (A\B)= card A - card B. Пусть А={ a,b,c }, В={ a,b,c }, А\В=ÆÞ card (A\B)=0. card A=3, card B=3. card A - card B=3-3=0. Итак, card (A\B)=0. card A - card B.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. Заданы множества А и В. Выписать все элементы множества АхВ. 1) А={ a,b,c }, B={ d,t }, 2) A={1,2,3}, B={2,3,6}.
Задача 2*. Верно ли, что мощность объединения двух множеств равна сумме их мощностей? В каких случаях это верно?
Задача 3*. Верно ли, что мощность пересечения двух множеств равна произведению их мощностей? В каких случаях это верно?
Основы комбинаторики
Комбинаторика – раздел математики, который занимается подсчетом числа способов (вариантов) совершить то или иное действие.
Основы формулы комбинаторики
| Формулы | Без повторений | С повторениями |
| Размещения | 
| 
|
| Перестановки |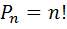 
| 
|
| Сочетания |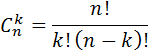 
| 
|
Правило суммы: если объект А может быть выбран m способами, объект В другими n способами и их одновременный выбор невозможен, то выбор «А или В» можно выбрать m+n способами.
Правило произведения: если объект А может быть выбран m способами, при любом выборе А объект В может быть выбран n способами, то выбор А и В можно выбрать m x n способами.
ПРИМЕР РЕШЕНИЯ ЗАДАЧ
Задача 1. Бросают две игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков?
Решение. Пусть m – число возможностей для выпадения четного числа на одной кости, n – число возможностей для выпадения нечетного числа. Здесь m=n=3. По правилу произведения количество выпадения четных чисел, как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных и двух нечетных чисел будет 18.
Задача 2. Сколько существует способов, чтобы расположить на полке 10 различных книг?
Решение. При выборе 10 различных книг для расположения на полке важен порядок, то есть речь идет о перестановках без повторений, следовательно, используем формулу Pn=n! n=10 Þ P10=10!=10×9×8×7×6×5×4×3×2×1=3628800.
Задача 3. Группа из 15 человек выиграла 3 различные книги. Сколькими способами можно распределить эти книги среди группы?
Решение. Выиграны три различные книги и при их распределении среди участников группы важен порядок. Это размещение без повторений, используем формулу
, n=15, k=3. Итак, 
Задача 4. Группа из 15 человек выиграла 3 одинаковые книги. Сколькими способами можно распределить эти книги?
Решение. При распределении книг (они одинаковые) между участниками группы порядок не важен. Мы имеем дело с сочетаниями без повторений. Используем формулу
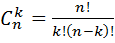n=15, k=3. Итак, 
Задача 5. Сколько различных слов можно получить, переставляя буквы в слове «м а т е м а т и к а»?
Решение. Имеется 10 букв: букв «м» - 2, «а» - 3, «т» - 2, «е» - 1, «к» - 1. Итак, имеют место перестановки с повторениями, следовательно, используем формулу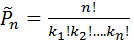 
для подсчета количества слов, составленных из букв слова «м а т е м а т и к а». n=10, k1=2, k2=3, k3=2, k4=1, k5=1, k6=1, 
.
Задача 6. Сколько пятизначных чисел можно составить, используя цифры: 1) 3,5,7,9; 2) 0;1;2.
Решение. 1. Все пятизначные числа, составленные из цифр 3,5,7,9, отличаются друг от друга либо порядком их следования (35579 и 53579), либо самими цифрами (35795 и 57733). Следовательно, они являются размещениями из 4 элементов по 5 с повторениями, т.е. 
. Итак, искомое число пятизначных чисел равно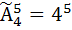 
=1024.
2. Если пятизначные числа состоят из цифр 0,1,2, то первую цифру слева можно выбрать либо 1, либо 3 (0 не может занимать первую позицию). Таким образом, таких чисел будет 
=162.
Задача 7. На почте пять видов открыток к Новому году. Сколькими способами из них можно выбрать семь открыток?
Решение. Рассматриваемое множество состоит из 5 различных элементов, а выборки имеют объем, равный 7. Поскольку порядок выбора открыток к Новому году не играет роли, то искомое число возможностей составит набор поздравительных открыток к Новому году равно числу сочетаний с повторениями:
n=5, k=7. 
=330.
