ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Любое движение твердого тела может быть представлено как наложение двух основных видов движения – поступательного и вращательного.
При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие этого скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому для описания движения тела достаточно знать движение одной его точки, например, центра масс.
При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Для описания вращательного движения необходимо знать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
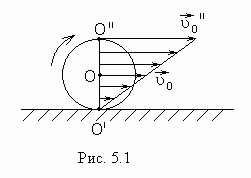Рассмотрим плоское движение твердого тела (при таком движении все точки тела перемещаются в параллельных плоскостях). Примером такого движения является качение цилиндра по плоскости (рис.5.1).
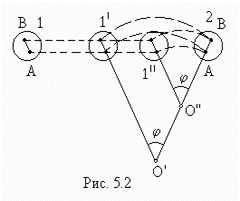Произвольное перемещение твердого тела из положения 1 в положение 2 (рис.5.2) можно представить как сумму двух перемещений -–поступательного перемещения из положения 1 в положение 1¢ или 1² и поворота вокруг оси О¢ или О². Такое разбиение перемещения на поступательное и вращательное может быть осуществлено бесчисленным множеством способов, однако в любом случае производится поворот на один и тот же угол 
.
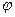Элементарное перемещение любой точки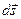 
равно векторной сумме поступательного 
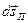и вращательного 
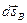перемещений: 
.
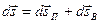При этом 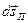для всех точек тело одинаково. Разделив обе части на промежуток времени 
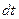, за который совершено перемещение 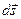, получаем скорость выбранной точки относительно неподвижной системы отсчета
где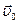 
- одинаковая для всех точек тела скорость поступательного движения, 
- различная для разных точек тела скорость, обусловленная вращением. Для точки с радиус-вектором 
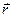эта скорость равна 
. Тогда скорость точки при сложном движении равна 
Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг некоторой оси, называемой мгновенной осью вращения. Эта ось может лежать в пределах тела, либо вне его. Положение мгновенной оси вращения относительно неподвижной системы отсчета и относительно самого тела меняется со временем. В случае катящегося цилиндра (рис.5.1) мгновенная ось О ¢ совпадает с линией касания цилиндра с плоскостью. При качении цилиндра мгновенная ось перемещается по плоскости (т.е. относительно неподвижной системы отсчета) и по поверхности цилиндра.
Скорости всех точек тела для каждого момента времени можно считать обусловленными вращением вокруг соответствующей мгновенной оси. Тогда плоское движение можно рассматривать как ряд последовательных элементарных вращений вокруг мгновенных осей.
При неплоском движении элементарное перемещение тела можно представить как поворот вокруг мгновенной оси лишь в том случае, когда векторы 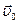и 
взаимно перпендикулярны. Если угол между этими векторами отличен от 
, движение тела в каждый момент времени является наложением двух движений – вращения вокруг некоторой оси и поступательного движения вдоль этой оси.
