Изучите теоретический материал по учебной литературе: [1, с.269–281]; [2, с.324–631]; [3, с.293–300] и ответьте на следующие вопросы:
1. Какие цепи относятся к цепям с распределенными параметрами?
2. Какие длинные линии называются однородными?
3. Что такое первичные параметры?
4. Как записать систему уравнений однородной длинной линии для мгновенных значений токов и напряжений.
5. Какими параметрами характеризуют однородную длинную линию в установившемся синусоидальном режиме?
6. Что такое вторичные параметры однородной длинной линии?
7. Как связано значение волнового сопротивления однородной длинной линии с ее первичными параметрами?
8. Как связано значение коэффициента распространения однородной длинной линии с ее первичными параметрами?
9. Какой физический смысл имеют вещественная и мнимая составляющие коэффициента распространения?
10. Как записать выражение для мгновенного значения бегущей волны напряжения и тока?
11. В каком случае в этих выражениях будут отсутствовать составляющие, определяющие отражение волны напряжения или тока?
12. Какие однородные длинные линии называются неискажающими?
13. Как для неискажающей длинной линии волновое сопротивление связано со значениями ее первичных параметров?
14. Как связано значение коэффициента затухания (ослабления) неискажающей длинной линии со значениями ее первичных параметров?
15. Как связано значение коэффициента фазы неискажающей длинной линии со значениями ее первичных параметров?
16. Как записать выражение, определяющее зависимость входного напряжения от выходного напряжения для однородной линии, разомкнутой на конце?
17. Как записать выражения, определяющие связь входных значений напряжения и тока с током на выходе линии, короткозамкнутой на конце?
18. Как связано входное сопротивление линии, разомкнутой на конце, со значениями ее вторичных параметров?
В качестве подготовительной рекомендуется выполнить задачу 13.1.
При изучении теоретических вопросов следует обратить внимание на то, что в данных методических указаниях в качестве цепи с распределенными параметрами рассматривается однородная двухпроводная линия, параметры которой равномерно распределены вдоль всей длины линии.
Распределенные параметры однородной линии на единицу ее длины обозначены как 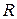 – активное сопротивление двух проводов,
– активное сопротивление двух проводов,  – индуктивность,
– индуктивность, 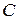 – емкость,
– емкость,  – проводимость изоляции между проводами. Эти параметры носят название первичных параметров.
– проводимость изоляции между проводами. Эти параметры носят название первичных параметров.
В установившемся синусоидальном режиме однородная линия может быть охарактеризована с помощью вторичных параметров: волнового сопротивления 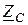 и коэффициента распространения
и коэффициента распространения 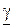 .
.
Волновое сопротивление – это отношение комплексного напряжения к комплексному току бегущей вдоль линии прямой (пр) или обратной (об) электромагнитной волны, Ом
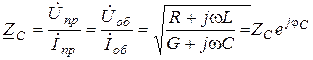 . (13.1)
. (13.1)
Коэффициент распространения, км 
 . (13.2)
. (13.2)
Этот коэффициент характеризует изменение модуля и аргумента комплексной амплитуды бегущей вдоль линии синусоидальной волны тока или напряжения при перемещении волны на единицу длины линии. Вещественная часть этого коэффициента  – коэффициент затухания (ослабления) показывает уменьшение амплитуды бегущей волны тока или напряжения на единицу длины. Коэффициент фазы
– коэффициент затухания (ослабления) показывает уменьшение амплитуды бегущей волны тока или напряжения на единицу длины. Коэффициент фазы  характеризует изменение фазы бегущей волны тока или напряжения на единицу длины и определяет такие параметры бегущих волн, как фазовая скорость
характеризует изменение фазы бегущей волны тока или напряжения на единицу длины и определяет такие параметры бегущих волн, как фазовая скорость 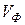 и длина волны
и длина волны 
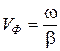 , (13.3)
, (13.3)
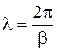 . (13.4)
. (13.4)
Анализ соотношений (13.1) и (13.2) показывает элементарную связь вторичных параметров с первичными. Действительно,
 , (13.5)
, (13.5)
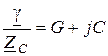 . (13.6)
. (13.6)
Напряжение и ток в любой точке линии можно рассчитать по следующим уравнениям
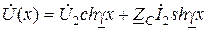 ,
, 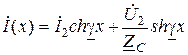 , (13.7)
, (13.7)
где x – расстояние, отсчитываемое от конца линии;
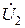 и
и 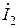 – напряжение и ток нагрузки.
– напряжение и ток нагрузки.
Входное сопротивление линии можно определить как отношение комплексного значения напряжения к комплексному значению тока в начале линии
 , (13.8)
, (13.8)
где 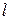 – длина линии;
– длина линии;
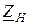 – комплексное сопротивление нагрузки.
– комплексное сопротивление нагрузки.
Входное сопротивление линии длиной 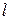 в режиме короткого замыкания (к.з.)
в режиме короткого замыкания (к.з.) 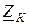 можно определить как
можно определить как
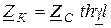 , (13.9)
, (13.9)
а входное сопротивление этой линии в режиме холостого хода 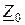 :
:
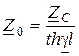 . (13.10)
. (13.10)
Анализ соотношений (13.9) и (13.10) показывает возможность нахождения вторичных параметров линии 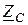 и
и 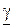 через ее входные сопротивления в режимах холостого хода и короткого замыкания:
через ее входные сопротивления в режимах холостого хода и короткого замыкания:
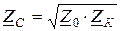 , (13.11)
, (13.11)
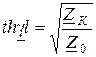 . (13.12)
. (13.12)
Неискажающая линия – это линия, в которой коэффициент ослабления и фазовая скорость не зависят от частоты синусоидального тока. Это обеспечивается определенным соотношением между первичными параметрами
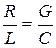 . (13.13)
. (13.13)
При этом волновое сопротивление 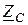 – вещественное число:
– вещественное число:
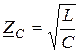 ,
, 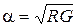 ,
, 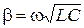 ,
, 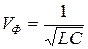 . (13.14)
. (13.14)
Линия без потерь – это линия, в которой параметры 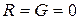 .
.
Для такой линии:
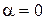 ,
, 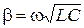 ,
, 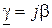 ,
, 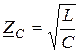 ,
, 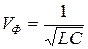 . (13.15)
. (13.15)
В уравнениях, описывающих распределение напряжения и тока вдоль линии, гиперболические функции заменяются круговыми:
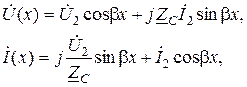 (13.16)
(13.16)
а входное сопротивление линии определяется как
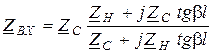 . (13.17)
. (13.17)
В выражении коэффициента распространения 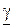 коэффициент ослабления
коэффициент ослабления  измеряется в неперах, а коэффициент фазы
измеряется в неперах, а коэффициент фазы  – в радианах. При вычислении круговых функций аргумент удобно иногда вычислять в градусах, тогда делается пересчет: 1 рад – 57,3
– в радианах. При вычислении круговых функций аргумент удобно иногда вычислять в градусах, тогда делается пересчет: 1 рад – 57,3 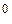 .
.
Обратим внимание на то, что при анализе различных режимов работы длинных линий с потерями приходится сталкиваться с необходимостью вычисления гиперболических функций с комплексными аргументами.
Приведем для удобства некоторые формулы.
Гиперболический синус
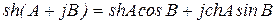 . (13.18)
. (13.18)
Гиперболический косинус
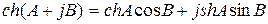 . (13.19)
. (13.19)
Гиперболический тангенс
 . (13.20)
. (13.20)
Результат, полученный при таком способе вычисления гиперболического тангенса, можно использовать для определения комплексного аргумента 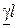 по известному значению гиперболического тангенса. Действительно, из формулы (13.20) следует
по известному значению гиперболического тангенса. Действительно, из формулы (13.20) следует
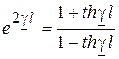 . (13.21)
. (13.21)
Иногда удобно гиперболический тангенс комплексного аргумента представить
 , (13.22)
, (13.22)
где
 ,
, 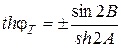 . (13.23)
. (13.23)
З а д а ч а 13. 1
По заданным в табл. 13.1 первичным параметрам длинной однородной линии определите волновое сопротивление и коэффициент распространения. Эти первичные параметры соответствуют параметрам воздушных двухпроводных линий связи с медными или стальными проводами и коаксиальных кабелей с медными жилами.
З а д а ч а 13. 2
По первичным параметрам высоковольтных линий электропередач, приведенным в табл. 13.2, определите их волновое сопротивление и коэффициенты распространения. Частота питающего напряжения  =50 Гц.
=50 Гц.
Таблица 13.1
Исходные данные к задаче 13.1
| Вариант | 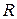
| 
| 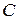
| 
| 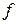
|
| Ом/км | мГн/км | нФ/км | мкСм/км | Гц | |
| 8,4 | 7,8 | 0,5 | |||
| 8,3 | 8,1 | 0,6 | |||
| 8,0 | 8,2 | 0,6 | |||
| 7,9 | 8,3 | 0,6 | |||
| 6,0 | 6,0 | 0,7 | |||
| 5,8 | 5,9 | 0,65 | |||
| 5,6 | 5,9 | 0,8 | |||
| 8,9 | 6,3 | 0,7 | |||
| 8,8 | 6,0 | 0,75 | |||
| 8,5 | 6,5 | 0,72 | |||
| 8,4 | 6,2 | 0,71 | |||
| 3,4 | 6,2 | 0,65 | |||
| 0,6 | 32,5 | 0,7 | |||
| 0,65 | 0,65 | ||||
| 0,65 | 0,7 | ||||
| 0,7 | 0,7 | ||||
| 0,55 | 0,65 | ||||
| 2,84 | 1,94 | 6,35 | 0,7 | ||
| 2,80 | 1,9 | 6,0 | 0,7 | ||
| 2,90 | 1,95 | 6,5 | 0,7 | ||
| 2,80 | 1,89 | 5,9 | 0,65 | ||
| 2,85 | 1,75 | 5,95 | 0,67 | ||
| 2,95 | 1,98 | 6,9 | 0,69 | ||
| 2,99 | 1,99 | 6,89 | 0,68 | ||
| 3,00 | 2,05 | 7,05 | 0,72 | ||
| 2,85 | 2,15 | 7,12 | 0,75 | ||
| 8,8 | 6,3 | 0,7 | |||
| 8,9 | 6,35 | 0,72 | |||
| 8,75 | 6,25 | 0,72 | |||
| 0,6 | 0,7 |
З а д а ч а 13. 3
Определите первичные параметры однородной линии, если известны ее волновое сопротивление 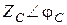 , коэффициент распространения
, коэффициент распространения 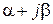 и частота
и частота 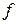 . Данные приведены в табл. 13.3.
. Данные приведены в табл. 13.3.
Таблица 13.2
Исходные данные к задаче 13.2
| Вариант | 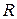
| 
| 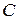
| 
|
| Ом/км | мГн/км | нФ/км | мкСм/км | |
| 0,08 | 1,27 | 8,3 | 0,04 | |
| 0,09 | 1,26 | 8,36 | 0,041 | |
| 0,085 | 1,28 | 8,23 | 0,045 | |
| 0,09 | 1,27 | 8,3 | 0,044 | |
| 0,095 | 1,29 | 8,17 | 0,048 | |
| 0,1 | 1,30 | 8,1 | 0,05 | |
| 0,15 | 1,31 | 8,05 | 0,06 | |
| 0,12 | 1,32 | 7,78 | 0,07 | |
| 0,11 | 1,33 | 7,92 | 0,08 | |
| 0,13 | 1,34 | 7,87 | 0,09 | |
| 0,14 | 1,35 | 7,81 | 0,1 | |
| 0,15 | 1,36 | 7,75 | 0,12 | |
| 0,16 | 1,37 | 7,69 | 0,14 | |
| 0,17 | 1,38 | 8,3 | 0,16 | |
| 0,18 | 1,39 | 8,35 | 0,18 | |
| 0,19 | 1,40 | 8,36 | 0,19 | |
| 0,2 | 1,41 | 8,37 | 0,2 | |
| 0,21 | 1,42 | 8,38 | 0,3 | |
| 0,22 | 1,43 | 8,39 | 0,4 | |
| 0,081 | 1,44 | 8,4 | 0,5 | |
| 0,082 | 1,45 | 8,41 | 0,45 | |
| 0,091 | 1,44 | 8,42 | 0,35 | |
| 0,092 | 1,43 | 8,43 | 0,25 | |
| 0,095 | 1,42 | 8,44 | 0,26 | |
| 0,096 | 1,41 | 8,45 | 0,195 | |
| 0,097 | 1,40 | 8,5 | 0,19 | |
| 0,098 | 1,39 | 8,6 | 0,21 | |
| 0,099 | 1,38 | 8,7 | 0,22 | |
| 0,11 | 1,37 | 8,8 | 0,23 | |
| 0,12 | 1,36 | 8,9 | 0,24 |
З а д а ч а 13. 4
Определите вторичные параметры линии (ее волновое сопротивление и коэффициент распространения) по данным опыта холостого хода и короткого замыкания. Значения входных сопротивлений линии в режимах холостого хода (х.х.)  и короткого замыкания (к.з.)
и короткого замыкания (к.з.)  , а также длина линии
, а также длина линии 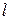 приведены в табл. 13.4.
приведены в табл. 13.4.
З а д а ч а 13. 5
Как надо изменить индуктивность  однородной линии, чтобы она стала неискажающей? Первичные параметры линии приведены в табл. 13.1.
однородной линии, чтобы она стала неискажающей? Первичные параметры линии приведены в табл. 13.1.
З а д а ч а 13. 6
Для линии длиной 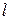 =55 км, параметры которой, входное напряжение и режим работы заданы в табл. 13.3, определите ток в начале линии.
=55 км, параметры которой, входное напряжение и режим работы заданы в табл. 13.3, определите ток в начале линии.
З а д а ч а 13. 7
Линия длиной 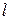 =20 км, параметры которой и входное напряжение приведены в табл. 13.3, нагружена на волновое сопротивление. Определите комплексное действующее значение входного тока
=20 км, параметры которой и входное напряжение приведены в табл. 13.3, нагружена на волновое сопротивление. Определите комплексное действующее значение входного тока 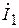 , а также комплексные действующие значения напряжения и тока нагрузки
, а также комплексные действующие значения напряжения и тока нагрузки  и
и 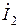 .
.
З а д а ч а 13. 8
Для линии в задаче 13.7 запишите мгновенное значение волн напряжения и тока.
З а д а ч а 13. 9
Однородная линия без потерь находится в режиме короткого замыкания. Определите входное сопротивление линии длиной  и
и 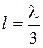 , где
, где  – длина волны. Параметры линии приведены в табл. 13.5.
– длина волны. Параметры линии приведены в табл. 13.5.
Таблица 13.3
Исходные данные к задачам 13.3, 13.6, 13.7
| Вариант | 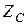
| 
| 
| 
| 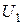
| 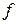
| Режим |
| Ом | град | х10  Нп/км Нп/км
| х10  рад /км рад /км
| В | Гц | ||
| –41 | 4,12 | 4,7 | к.з | ||||
| –25 | 1,59 | 3,16 | х.х | ||||
| –22 | 1,61 | 3,64 | к.з | ||||
| –21 | 1,67 | 4,06 | х.х | ||||
| –10,49 | 0,27 | 1,25 | к.з | ||||
| –9,84 | 0,29 | 1,45 | х.х | ||||
| –8,8 | 0,29 | 1,65 | к.з | ||||
| –10 | 0,29 | 1,42 | х.х | ||||
| –12,69 | 0,27 | 1,04 | к.з | ||||
| –14 | 0,26 | 0,87 | х.х | ||||
| –11,7 | 0,28 | 1,14 | к.з | ||||
| –8,5 | 0,26 | 1,50 | х.х | ||||
| –7,5 | 0,27 | 1,78 | к.з | ||||
| –41 | 3,63 | 4,15 | х.х | ||||
| –42 | 3,28 | 3,57 | к.з | ||||
| –42 | 3,59 | 3,94 | х.х | ||||
| –41 | 3,50 | 4,02 | к.з | ||||
| –41 | 4,15 | 4,73 | х.х | ||||
| –27,36 | 1,49 | 2,66 | к.з | ||||
| –30,37 | 1,47 | 2,27 | х.х | ||||
| –25,17 | 1,61 | 3,18 | к.з | ||||
| –22,18 | 1,55 | 3,51 | х.х | ||||
| –21 | 1,67 | 4,03 | к.з | ||||
| –26,25 | 0,74 | 1,26 | х.х | ||||
| –11 | 0,87 | 4,12 | к.з | ||||
| –12,24 | 0,91 | 3,86 | х.х | ||||
| –11,2 | 0,98 | 4,67 | к.з | ||||
| –12,82 | 1,01 | 4,18 | х.х | ||||
| –14,49 | 1,03 | 3,73 | к.з | ||||
| –16,92 | 1,03 | 3,20 | х.х |
З а д а ч а 13. 10
Линия без потерь, параметры которой приведены в табл. 13.5, работает в режиме холостого хода при 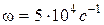 . Определите при какой наименьшей длине линия эквивалентна по своему сопротивлению:
. Определите при какой наименьшей длине линия эквивалентна по своему сопротивлению:
1) емкости 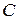 = 110 нФ,
= 110 нФ,
2) индуктивности  = 3мГн.
= 3мГн.
Таблица 13.4
Исходные данные к задаче 13.4
| Вариант | 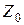
| 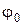
| 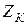
| 
| 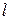
|
| Ом | град | Ом | град | км | |
| 1146,19 | –79,09 | 1143,81 | 45,25 | 24,5 | |
| 1090,55 | –80,88 | 1083,96 | 51,04 | ||
| 1027,14 | –81,29 | 1060,81 | 55,65 | ||
| 1028,04 | –82,71 | 1006,08 | 60,39 | 16,7 | |
| 1079,16 | –81,81 | 1026,77 | 57,33 | ||
| 1038,16 | –82,38 | 1028,50 | 60,38 | ||
| 1317,88 | –69,89 | 1304,93 | 17,39 | ||
| 1416,07 | –76,90 | 1368,34 | 34,94 | ||
| 1485,29 | –75,92 | 1410,46 | 31,56 | ||
| 1433,32 | –73,32 | 1481,07 | 22,98 | ||
| 2084,53 | –75,57 | 1446,28 | 14,83 | ||
| 1566,44 | –72,40 | 1570,28 | 17,68 | 29,5 | |
| 351,84 | –69,35 | 352,16 | –12,55 | 16,6 | |
| 379,56 | –69,46 | 378,38 | –12,18 | 19,5 | |
| 470,61 | –68,76 | 472,19 | –15,24 | ||
| 497,98 | –68,81 | 497,18 | –15,59 | ||
| 357,75 | –69,60 | 364,26 | –12,32 | 18,8 | |
| 566,95 | –83,87 | 561,07 | 68,87 | ||
| 576,44 | –82,81 | 579,18 | 65,79 | 52,4 | |
| 572,48 | –80,30 | 579,50 | 56,90 | ||
| 515,27 | –78,41 | 603,36 | 50,41 | ||
| 575,39 | –79,71 | 575,45 | 54,33 | 75,5 | |
| 594,21 | –82,74 | 519,13 | 62,68 | ||
| 555,33 | –63,10 | 549,50 | 65,50 | 47,5 | |
| 558,26 | –82,04 | 558,56 | 62,35 | ||
| 573,18 | –81,13 | 571,52 | 60,15 | 62,75 | |
| 1419,35 | –76,94 | 1357,09 | 34,66 | ||
| 1475,42 | –76,31 | 1375,55 | 31,43 | ||
| 1509,73 | –73,77 | 1501,08 | 23,77 | 24,75 | |
| 354,70 | –69,29 | 356,02 | –12,73 | 16,75 |
З а д а ч а 13. 11
Для линии, параметры которой приведены в табл. 13.5, постройте график распределения действующего значения напряжения вдоль линии  . Длина линии
. Длина линии 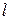 равна длине волны и линия нагружена на активное сопротивление
равна длине волны и линия нагружена на активное сопротивление 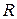 : 1)
: 1)  , 2)
, 2) 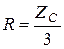 , 3)
, 3)  . Напряжение
. Напряжение 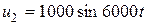 ,В.
,В.
Таблица 13.5
Исходные данные к задачам 13.9, 13.10, 13.11
| Вариант | 
| 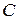
| вариант | 
| 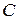
|
| мГн/км | нФ/км | мГн/км | нФ/км | ||
| 0,2 | 0,33 | ||||
| 0,25 | 0,34 | ||||
| 0,3 | 0,35 | ||||
| 0,35 | 2,5 | 0,36 | |||
| 0,4 | 2,5 | 0,37 | |||
| 0,1 | 0,38 | ||||
| 0,15 | 0,39 | ||||
| 0,16 | 0,4 | ||||
| 0,17 | 0,41 | ||||
| 0,25 | 0,42 | ||||
| 0,15 | 0,43 | ||||
| 0,16 | 0,44 | ||||
| 0,29 | 0,45 | ||||
| 0,31 | 0,46 | ||||
| 0,32 | 0,47 |
З а д а ч а 13. 12
Вычислите входное сопротивление линии без потерь при коротком замыкании, если ее волновое сопротивление  , длина линии
, длина линии 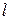 и длина волны
и длина волны  приведены в табл. 13.5.
приведены в табл. 13.5.
Таблица 13.6
Исходные данные к задачам 13.12, 13.13
| Вариант | 
| 
| 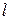
| Вариант | 
| 
| 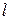
|
| Ом | м | м | Ом | м | м | ||
З а д а ч а 13. 13
Определите входное сопротивление линии без потерь при холостом ходе. Волновое сопротивление  , длина линии
, длина линии 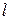 и длина волны
и длина волны  приведены в табл. 13.6.
приведены в табл. 13.6.
З а д а ч а 13. 14
Определите амплитуду тока на заданном расстоянии 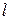 от разомкнутого конца линии без потерь, если известны ее волновое сопротивление
от разомкнутого конца линии без потерь, если известны ее волновое сопротивление  , действующее значение напряжения
, действующее значение напряжения 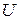 на разомкнутом конце и частота
на разомкнутом конце и частота 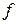 , приведенные в табл. 13.7.
, приведенные в табл. 13.7.
Таблица 13.7
Исходные данные к задаче 13.14
| Вариант | 
| 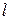
| 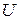
| 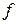
| Вариант | 
| 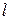
| 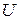
| 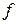
|
| Ом | м | В | 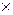 10 10 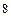 Гц Гц
| Ом | м | В | 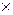 10 10 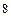 Гц Гц
| ||
| 0,35 | |||||||||
| 0,5 | |||||||||
| 1,5 | 3,5 | 1,2 | |||||||
| 2,5 | |||||||||
| 0,5 | 2,5 | ||||||||
| 1,5 | 0,1 | ||||||||
| 2,5 | 0,15 | ||||||||
| 2,5 | 1,5 | ||||||||
| 1,8 | |||||||||
| 2,5 | |||||||||
| 1,3 | 1,5 | ||||||||
| 4,5 | 1,8 | ||||||||
| 2,5 | 0,7 |






