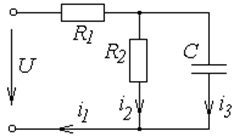
Пусть для цепи (рис. 8.1) известны параметры  Гн, С =
Гн, С = 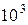 мкФ,
мкФ,  Ом, U =100 B. Необходимо определить закон изменения в переходном процессе функции
Ом, U =100 B. Необходимо определить закон изменения в переходном процессе функции  .
.
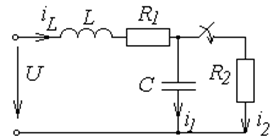
Рис. 8.1. Схема к примеру по расчету переходных процессов
методом переменных состояния
Построим нормальное дерево. Заметим, что при его построении учитываются все узлы графа, в том числе и устранимые. Обозначим ветви дерева сплошными линиями, а хорды – пунктирными.
Отметим на графе основные сечения (разрезы), перечислив их в порядке приоритетов ветвей дерева.

Рис. 8.2. Граф схемы рис. 8.1
Для основных разрезов составим систему уравнений по первому закону Кирхгофа, а для основных контуров – по второму.
 , (8.2)
, (8.2)
 , (8.3)
, (8.3)
 , (8.4)
, (8.4)
 , (8.5)
, (8.5)
 . (8.6)
. (8.6)
Из этих уравнений выбираем два уравнения (8.2) и (8.5), содержащие ток  и напряжение
и напряжение 
 ,
,
 .
.
Далее с помощью оставшихся уравнений системы выражаем токи и напряжения правой части этих двух уравнений через переменные состояния. Таким образом, получаем следующую систему уравнений:
 ,
,
 .
.
Следовательно

 +
+ 
 .
.
Здесь векторы и матрицы следующие
 ,
,  ,
, 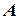 =
= 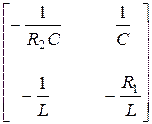 ,
,  =
=  ,
,  =
= 
Если искомой величиной является функция  , то
, то  . В соответствии с математической формулировкой задачи вектор Y также должен быть выражен через переменные состояния. Эти связи находятся из анализа той же системы уравнений (8.2)… (8.6). Для данного примера
. В соответствии с математической формулировкой задачи вектор Y также должен быть выражен через переменные состояния. Эти связи находятся из анализа той же системы уравнений (8.2)… (8.6). Для данного примера 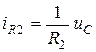 . Поэтому матрицы
. Поэтому матрицы  и
и  принимают вид
принимают вид
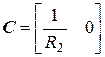 ,
,  .
.
Решение такой системы можно получить численным методом с помощью, например, пакета MathCad.
Для этого выполним операции перемножения и суммирования в правой части уравнения (8.1) и подставим численные значения параметров схемы. Получаем в системе (8.1) справа матрицу–столбец. Присвоим значения этого столбца матрице, которую обозначим как  .
.
 ,
,
где  и
и 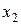 – элементы вектора
– элементы вектора  .
.
Для решения этой системы дифференциальных уравнений выберем метод Рунге – Кутта с переменным шагом. Для этого в пакете MathCad выбираем окна в следующем порядке: ФУНКЦИИ – дифференциальные уравнения – Rkadapt.
Для того чтобы воспользоваться этой функцией MathCad, необходимо задать вектор независимых начальных условий, который обозначим как  , указать начало
, указать начало  и конец
и конец 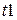 времени интегрирования, а также количество точек N, для которых проводится решение.
времени интегрирования, а также количество точек N, для которых проводится решение.
 .
.
Вектор – результат решения системы дифференциальных уравнений обозначим S (solving). Тогда ввод команды для решения будет выглядеть следующим образом:
 .
.
Выделим из матрицы решения S независимую переменную  и функции
и функции  и
и 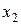 , учитывая, что аргумент расположен в первом столбце, а функции
, учитывая, что аргумент расположен в первом столбце, а функции  и
и 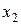 в последующих столбцах. Так для рассматриваемой схемы
в последующих столбцах. Так для рассматриваемой схемы

(здесь счет элементов матриц начинается с единицы).
Для того чтобы решить алгебраическую часть общей системы уравнений, надо искомую функцию выразить через полученные в результате интегрирования переменные состояния. Тогда искомый ток  найдем как
найдем как
 .
.
На рис. 8.3 представлен примерный вид окна пакета MathCad.
З а д а ч а 8. 1
Электрические цепи, схемы которых показаны на рис. 7.5, а параметры приведены в табл. 7.4, включаются под действие напряжения  В. Составьте систему уравнений, необходимых для расчета
В. Составьте систему уравнений, необходимых для расчета  методом переменных состояния.
методом переменных состояния.

|
Рис. 8.3. Общий вид окна при решении задачи с использованием
метода переменных состояния в пакете MathCad
З а д а ч а 8. 2
Составьте систему уравнений, необходимых для расчета указанных в табл. 8.3 величин методом переменных состояния.
З а д а ч а 8. 3
Для электрической схемы, соответствующей номеру варианта (табл. 8.4), параметры которой указаны в табл. 8.5, определите искомые ток и напряжение.
Таблица 8.2
Схемы к задаче 8.2
| № п/п | Схема | № п/п | Схема |

| 
| ||

| 
| ||

| 
| ||

| 
|
Таблица 8.3
Исходные данные к задаче 8.2
| Вариант | Схема из табл.8.2 | Искомые величины | Вариант | Схема из табл.8.2 | Искомые величины | Вариант | Схема из табл.8.2 | Искомые величины |

| 
| 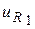
| ||||||

| 
| 
| ||||||

| 
| 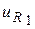
| ||||||

| 
| 
| ||||||

| 
| 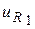
| ||||||

| 
| 
| ||||||

| 
| 
| ||||||

| 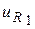
| 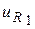
| ||||||

| 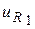
| 
| ||||||

| 
| 
|
Таблица 8.4
Схемы к задаче 8.3
| № п/п | Схема | № п/п | Схема |

| 
| ||

| 
| ||

| 
|
Таблица 8.5
Исходные данные к задаче 8.3
| Вариант | Схема из табл.8.4 | 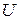
| 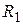
| 
| 
| 
| 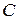
| Определить |
| В | Ом | Ом | Ом | мГн | мкФ | |||

| ||||||||

| ||||||||

| ||||||||
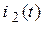
| ||||||||
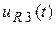
| ||||||||

| ||||||||

| ||||||||

| ||||||||
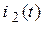
| ||||||||

| ||||||||
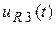
| ||||||||

| ||||||||

| ||||||||
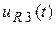
| ||||||||

| ||||||||

| ||||||||

| ||||||||
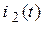
| ||||||||
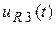
| ||||||||

| ||||||||

| ||||||||

| ||||||||
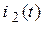
| ||||||||

| ||||||||

| ||||||||

| ||||||||
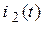
| ||||||||

| ||||||||

| ||||||||

|
ЗАНЯТИЕ 9






