| Курение | Пол | Итого | |
| м | ж | ||
| Курит | |||
| Не курит | |||
| Итого |
Данные таблицы 15 говорят о том, что в нашей совокупности имеется 90 мужчин, из которых 80 человек курят, и 10 женщин, среди которых 4 человека курящих и т.д.
Все известные коэффициенты связи для четырехклеточных таблиц основаны на сравнении произведений ad и bc. Если эти произведения близки друг к другу, то полагаем, что связи нет. Если они совсем не похожи – связь есть. Основано такое соображение на том, что равенство 
эквивалентно равенству 
, что, в свою очередь, означает пропорциональность столбцов (строк) нашей частотной таблицы, т.е отсутствие статистической связи. Чем более отличны друг от друга указанные произведения, тем менее пропорциональны столбцы (строки) и, стало быть, тем больше оснований имеется у нас полагать, что переменные связаны. Для обоснования этого утверждения могут быть использованы те же рассуждения, что были приведены выше. А именно, можно показать, что разница между наблюдаемой и теоретической частотой для левой верхней клетки нашей четырехклеточной частотной таблицы (нетрудно проверить, что наличие или отсутствие связи для такой таблицы определяется содержанием единственной клетки - при заданных маргиналах частоты, стоящие в других клетках, можно определить однозначно) равна величине [Кендалл, Стьюарт, 1973. С. 722]:
Коэффициенты, основанные на описанной логике, могут строиться по-разному. Но всегда они базируются либо на оценке разности (
), либо на оценке отношения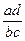 
. В первом случае об отсутствии связи будет говорить близость разности к нулю, во втором – близость отношения к единице. Естественно, ни разность, ни отношение не могут служить искомыми коэффициентами в “чистом” виде, поскольку их значения зависят от величин используемых частот. Требуется определенная нормировка. И, как мы уже оговаривали выше, желательно, чтобы искомые показатели связи находились либо в интервале от -1 до 1, либо – от 0 до 1, Возможны разные ее варианты. Это обуславливает наличие разных коэффициентов – показателей связи для четырехклеточных таблиц. Рассмотрим два наиболее популярных коэффициента.
Коэффициент ассоциации Юла:
и коэффициент контингенции
Коротко рассмотрим их основные свойства.
Оба коэффициента изменяются в интервале от -1 до +1 (значит, для них имеет смысл направленность связи; о том, что это такое в данном случае, пойдет речь ниже). Обращаются в нуль в случае отсутствия статистической зависимости, о котором мы говорили выше (независимость признаков связана с пропорциональностью столбцов таблицы сопряженности). А вот в единицу (или - 1) эти коэффициенты обращаются в разных ситуациях. Они схематично отражены ниже.
| Свойства коэффициентов: | Q = 1 | Q = -1 | Ф = 1 | F = -1 | ||||
| Отвечающие им виды таблиц | a | b | a | b | ||||
| c | d | c | d | d | c | |||
| a | b | a | b | |||||
| d | c | |||||||
| (а) | (б) | (в) | (г) |
Рис. 16. Схематическое изображение свойств коэффициентов Q и Ф.
Таким образом, мы видим, что Q обращается в 1, если хотя бы один элемент главной диагонали частотной таблицы равен 0. Для обращения же в 1 коэффициента F необходимо обращение в 0 обоих элементов главной диагонали. Нужны ли социологу оба коэффициента? Покажем, что каждый из них позволяет выделять свои закономерности. Или, как мы говорили выше – за каждым из них стоит своя модель изучаемого явления, свое понимание связи, выделение как бы одной стороны того, что происходит в реальности. Постараемся убедить читателя, что социолога должны интересовать обе эти стороны.
Предположим, что в нашем распоряжении имеется лишь коэффициент F и мы даем задание ЭВМ для каких-то массивов данных выдать нам все такие четырехклеточные таблицы, для которых этот коэффициент близок к единице (может быть, мы хотим найти все те признаки, для которых имеется связь для респондентов некоторой фиксированной совокупности, а, может быть – изучаем, для каких совокупностей респондентов имеется сильная связь между какими-то конкретными признаками). ЭВМ выдаст нам набор таблиц типа (в) или (г). Мы будем знать, к примеру, что имеются группы респондентов, для которых имеется сильная связь между полом и курением: все мужчины курят, а все женщины не курят (что довольно распространено) или наоборот – все женщины курят, а мужчины – нет (что имеет место, скажем, для некоторых индейских племен). Но мы “не заметим”, что для каких-то групп все мужчины курят, в то время как среди женщин встречаются и курящие, и не курящие, либо все женщины не курят, хотя мужчины ведут себя по-разному - могут и курить, и не курить (случай (а)). Думается, что не требует особого доказательства утверждение о том, что социолог, не умеющий выискивать подобные ситуации, рискует много потерять. Аналогичное утверждение справедливо и относительно ситуаций, обохзначенных буквой (б).
Другими словами, не используя коэффициент Q, социолог рискует не заметить интересующие его закономерности. Перефразируя сказанное выше вспомнив, что связь также имеет отношение и к прогнозу, отметим, что эти не замеченные закономерности отвечают ситуациям, когда мы по одному значению первого признака можем прогнозировать значение второго, а по другому значению не можем: скажем, зная, что респондент - мужчина, мы с полной уверенностью можем сказать, что он курит, а зная, что респондент - женщина - никакого прогноза, вообще говоря, делать не можем (нижняя таблица случая (а)). Вряд ли можно сомневаться, что выявление и такой “половинчатой” возможности прогноза для социолога может быть полезной.
Рассмотрим теперь вопрос: не можем ли мы обойтись без коэффициента F? Представляется очевидным отрицательный ответ на него: выявляя значимые ситуации только с помощью Q, мы можем “за деревьями не увидеть леса” - не заметить, что в отдельных случаях мы может прогнозировать не только по одному значению того или иного признака, но и по другому тоже.
Описанное различие между коэффициентами Q и Ф нашло свое отражение в терминологии. Та связь, которую отражает Q, была названа полной, а та, которую отражает Ф, - абсолютной.
Еще раз определим эти виды связи, несколько видоизменив формулировку. Для этого вспомним, что, зная маргиналы четырехклеточной таблицы сопряженности, о связи между двумя дихотомическими признаками можно судить по одной частоте. Чаще всего для этого используют n11. Обозначим отвечающие этой частоте значения наших признаков через А и В. Например, А означает “мужчина”, а В – “курит”. В таком случае говорят, что связь между А и В полная, если все А являются одновременно В, несмотря на то, что не все В являются одновременно А (все мужчины курят, но не все курящие являются мужчинами). Если же все А являются одновременно В и все В являются одновременно А (т.е. если все мужчины курят и все курящие – мужчины), то связь называется абсолютной. Иногда для обозначения тех же свойств рассматриваемой связи используют иную терминологию – говорят, что Q измеряет одностороннюю связь, а Ф – двустороннюю.
Поясним теперь, в чем смысл знака рассматриваемой связи. Для этого заметим, что приведенные выше рассуждения можно переформулировать, говоря не о том, что все А являются одновременно В, а о том, что свойства А и В сопрягаются друг с другом (таблица сопряженности потому так и названа, что ее придумали для того, чтобы изучать, какие значения разных признаков “ходят” вместе, сопрягаются друг с другом). Термины “положительный” и “отрицательный”, испоьзуемые для характеристики связи, носят весьма относительный характер: “положительность” означает, что какое-то значение первого признака сопрягается с одним значением другого, а “отрицательность” – с другим (при наличии положительной связи все мужчины курят, и при наличии отрицательной – все мужчины не курят).
Однако сказанное становится весьма нечетким утверждением при отсутствии нулевых клеток в таблице сопряженности. Например, трудно понять, с каким значением признака "курит – не курит" сопрягается мужской пол, если данные представлены таблицей:
Таблица 16
Частотная таблица для демонстрации отношения преобладаний
| Курение | Пол | Итого | |
| м | ж | ||
| Курит | |||
| Не курит | |||
| Итого |
С одной стороны, среди курящих больше женщин, чем мужчин. И среди женщин больше курящих, чем некурящих. Но правильно ли будет сказать, что свойство "курит" сопрягается с женским полом? Ведь если среди мужчин курящих в 2,5 раза (50:20) больше курящих, чем некурящих, то среди женщин – лишь в 2,25 раза (90:40). Строгое определение положительной и отрицательной связи можно дать с помощью введения понятия отношения преобладаний [Rudas,1998]:
или, в общем случае (обозначения – как в таблице 14):
Если отношение преобладания больше единицы, то связь называется положительной, если меньше единицы – то отрицательной. (Отношение преобладания обобщается на многомерный случай, о чем коротко пойдет речь в п. 2.3.5.).
И еще об одном очень важном моменте необходимо сказать. Если мы, используя обозначения 0 и 1 для значений наших признаков, будем интерпретировать эти обозначения как настоящие числа, то, как нетрудно проверить, вычисленный по обычным правилам коэффициент корреляции между признаками окажется равным Ф. Будучи обобщенным, этот факт имеет огромное значение для анализа данных. Дело в том, что одним из популярных способов создания возможности использования числовых математико-статистических методов для анализа номинальных (нечисловых!) данных является т.н. дихотомизация последних: замена (по определенным правилам) одного номинального признак таким количеством дихотомических, принимающих значения 0 и 1, сколько в этом признаке альтернатив и дальнейшая “работа” с этими 0 и 1 как с обычными числами. Этот подход не имеет строгого математического обоснования. Его “оправдание” состоит в том, что все числовые статистики, рассчитанные по обычным правилам, оказывается возможным разумно проинтерпретировать. Именно пример этого мы и видели выше: коэффициент корреляции, вычсленный для 0 и 1, оказался разумной величиной, совпал с Ф. Вернемся к этому в п. 2.6.3.
О коэффициентах связи для четырехклеточных таблиц можно прочесть в [Интерпретация и анализ..., 1987. С.29-30; Лакутин, Толстова, 1990, 1992; Паниотто, Максименко, 1982.С.84-93; Рабочая книга..., 1983. С.189; Статистические методы... 1979. С.116-117; Libetrau, 1989]
