Выражение представлений о связи через прогноз
Включение понятия прогноза в представление о связи между номинальными признаками представляется разумным: наверное, трудно возражать против того, чтобы признаки считались связанными, если значение одного признака позволяет достаточно хорошо предсказать значение другого. Поясним это на гипотетическом примере, который ниже мы будем неоднократно “эксплуатировать”. Заодно уточним только что сформулированное суждение.
Предположим, что мы изучаем жителей некоторого крупного города N от 20 лет и старше и что нас интересует связь между признаком “возраст”, рассматриваемым нами как номинальный и дихотомическим признаком со значениями “студент” – “не студент”.
(Напомним два принципиальных для социологии момента. Во-первых, определение типа шкалы для таких, казалось бы, “понятных” признаков, как возраст, далеко не всегда является ясным делом; причиной тому служит то, что их значения, как правило, интересуют исследователя не сами по себе, а лишь как показатели некоторых латентных переменных. Во-вторых, здесь мы отвлекаемся от сложной проблемы разбиения диапазона изменения непрерывного признака – предполагаем, что это сделано каким-либо адекватным решаемой задаче образом.)
Предположим, что распределение изучаемой совокупности по возрасту приблизительно равномерно, например, такое, какое изображено на рис. 14.
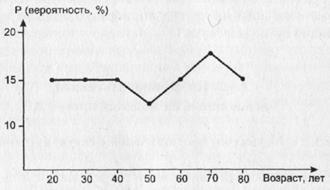
Рис.14. Гипотетическое распределение по возрасту жителей города N старше 20 лет
Интуитивно ясно, что в такой ситуации мы вряд ли сможем хорошо прогнозировать возраст респондента. Выбрав наугад (случайным образом) произвольного человека, мы примерно с одинаковой степенью уверенности можем полагать, что он имеет любой возраст: вероятность “наткнуться” на 20-летнего юношу такая же, как и на 80-летнего старика (подчеркнем своеобразие понимания нами термина “прогноз” - речь идет просто о том, что мы можем сказать о значении возраста для случайно выбранного респондента).
Другое дело, если мы рассмотрим только студентов. Ясно, что их распределение по возрасту будет резко отличаться от общего. Например, будет иметь вид, изображенный на рис. 15.
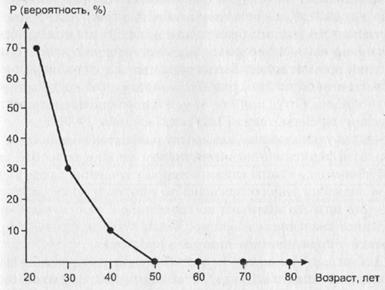
Рис. 15. Гипотетическое распределение по возрасту студентов города N старше 20 лет
Ясно, что теперь, случайным образом отобрав человека (студента), мы с уверенностью 90% (90 = 70 + 20) будем полагать, что его возраст не превысит 30 лет, вероятность же “попасть” на человека старше 40 лет практически равна нулю.
Итак, фиксировав значение “студент” второго рассматриваемого нами признака, мы явно улучшили возможность прогноза возраста жителей города. Наверное, на основе этого было бы разумно сделать вывод о наличии связи между признаком “возраст” и признаком “быть студентом”. Подчеркнем, что для того, чтобы сделать этот вывод, мы сравнили безусловное распределение признака “возраст” (рис. 14) с его условным распределением (рис. 15), когда условие состоит в фиксации значения “студент” второго признака. Возможность хорошего прогноза на основе знания условного распределения сама по себе (без ее сравнения с возможностью прогноза по безусловному распределению) ни о какой связи еще не говорит. Так, изучая только студентов, мы не можем говорить о связи пола и возраста на основе того,.что, отобрав только девушек, мы можем хорошо прогнозировать их возраст. Ведь, всего вероятнее, столь же хороший прогноз может быть осуществлен и для юношей, и для студентов вообще (т.е. для безусловного распределения). О соотношении безусловного и условного распределений при изучении связей см. также [Лакутин, Толстова, 1990].
Итак, будем считать, что смысл рассматриваемых (прогнозных) коэффициентов на интуитивном уровне ясен. Все такие коэффициенты должны служить мерой улучшения качества прогноза значения одного признака за счет получении сведений о значении другого признака по сравнению с тем случаем, когда последнее значение неизвестно. Такие коэффициенты и будем называть опирающимися на модель прогноза.
Для того, чтобы можно было практически пользоваться высказанными предположениями, необходимо их формализовать. Другими словами, необходимо четко понять, что такое прогноз и как именно на основе частотной таблицы мы можем судить о различии возможности прогноза для соответствующих условных и безусловных распределений. Формализация может быть разной. И, в первую очередь, неоднозначно может пониматься сам термин “прогноз”. Те известные коэффициенты связи, которые мы намереваемся рассмотреть, отличаются друг от друга как раз способом формализации этого понятия. Но прежде, чем переходить к описанию некоторых прогнозных коэффициентов, напомним, что проблема формализации содержательных представлений о “прогнозной” связи, вообще говоря, не исчерпывается рассуждениями о понимании прогноза и оценке его качества. Отметим также следующие три немаловажные момента.
Во-первых, глобальные коэффициенты связи по существу являются “усреднениями” всевозможных локальных коэффициентов. И подобные “усреднения” могут пониматься по-разному, выражаться разными формулами. Это также обусловливает наличие разных коэффициентов связи.
Во-вторых, возможность осуществления прогноза значений одного признака по значениям другого существенно зависит от того, значения какого признака прогнозируются. Скажем, значения первого могут хорошо прогнозироваться по значениям второго, а значения второго по значениям первого - очень плохо. Приведем простой, несколько утрированный пример. Пусть частотное распределение значений двух признаков имеет вид, представленный в табл. 12.
Таблица 12
Таблица сопряженности, иллюстрирующая несимметричность понятия “прогноз”
| X | Y | ||
Ясно, что по значению Х мы легко предсказываем значение Y. Обратное же не имеет места: если признак Y равен 3, то Х с одинаковым успехом (с равной вероятностью) может принимать значения 1 или 2. В таком случае возникает вопрос о построении коэффициентов, не симметричных относительно рассматриваемых признаков или, как говорят, коэффициентов, отражающих направленную связь – скажем, говорящих о том, появляется ли у нас новая информация о втором признаке при фиксации значения первого, но ничего не говорящих об обратной зависимости.
Актуальной является задача усреднения таких направленных коэффициентов для оценки ненаправленной связи. Обоснование соответствующей необходимости - примерно такое же, как обоснование необходимости использования глобальных коэффициентов наряду с локальными: с одной стороны. не имея коэффициентов направленной связи, мы можем упустить, не заметить важные причинно-следственные отношения, но, с другой – когда направленные связи не очень значимы, мы можем “за деревьями” не увидеть леса” – не уловить того, что, хотя каждая направленная связь не очень велика, в целом нельзя игнорировать взаимодействие рассматриваемых признаков.
О терминах: когда говорят о прогнозе значения признака Y по признаку Х, то Х называют независимой переменной, а Y – зависимой.
Перейдем к описанию наиболее известных коэффициентов, основанных на моделях прогноза.






