Сами значения рассматриваемого критерия непригодны для оценки связи между признаками, поскольку они зависят от объема выборки и других обстоятельств, носящих, вообще говоря случайный характер по отношению к силе измеряемой связи (о некоторых обстоятельствах подобного рода пойдет речь ниже). Так, величина критерия, например, равная 30, может говорить о большой вероятности наличия связи, если в клетках исходной частотной таблицы стоят величины порядка 10,20,30, и о ничтожной вероятности того же, если рассматриваемые частоты равны 1000, 2000, 3000 и т.д. В таких случаях возникает необходимость определенной нормировки найденного значения критерия – такого его преобразования, которое устранит описанную зависимость от случайных (для оценки связи) факторов.
Подчеркнем, что здесь речь идет о принципиальном моменте, часто возникающем при использовании в социологии разного рода статистических критериев, индексов и т.д. Всегда необходимо выяснять, не отражает ли используемый показатель что-либо случайное по отношению к изучаемому явлению и в случае наличия такого отражения осуществлять соответствующую нормировку показателя.
Принято нормировку, подобную описанной, осуществлять таким образом, чтобы нормированные коэффициенты изменялись либо от -1 до +1 (если имеет смысл противопоставление положительной и отрицательной направленности изучаемого с помощью рассматриваемого индекса явления, в нашем случае - связи), либо от 0 до 1 (если выделение положительной и отрицательной направленности явления содержательно бессмысленно).
Почеркнем, что приведение всех коэффициенту к одному и тому же интервалу является необходимым, но не достаточным условием, обеспечивающим возможность их сравнения. Если такого приведения не будет сделано, сравнение заведомо невозможно. Но и при его осуществлении сравнение тоже может оказаться бессмысленным. Об этом пойдет речь в п. 2.3.5.
Имеются разные подходы к требующейся нормировке. Наиболее известными являются такие, которые превращают критерий “Хи-квадрат” в известные коэффициенты, называемые обычно по именам впервые предложивших их авторов - Пирсона, Чупрова, Крамера. За этими коэффициентами утвердились постоянные обозначения, отвечающие первым буквам названных фамилий (коэффициент Чупрова отвечает немецкому tsch, коэффициент Крамера имеет два обозначения из-за известного различия букв, обозначающих звук “к” в разных языках):


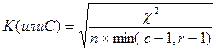
Опишем некоторые свойства этих коэффициентов. Начнем с тех, которые обычно оговариваются в литературе.
Все коэффициенты изменяются от 0 до 1 и равны нулю в случае полной независимости признаков (в описанном выше смысле). Как и критерий “хи-квадрат”, эти показатели являются симметричными относительно наших признаков: с их помощью нельзя выделить зависимую и независимую переменную, на основе их анализа нельзя говорить о том, какая переменная на какую "влияет".
Обычно в качестве недостатка коэффициента Пирсона Р (предложенного в литературе первым) упоминается зависимость его максимальной величины от размера таблицы (максимум Р достигается при c=r, но величина максимального значения изменяется с изменением числа категорий: при с=3 значение Р не может быть больше 0,8, при с=5 максимальное значение Р равно 0,89 и т.д. [ Интерпретация и анализ..., 1987. С.31]). Естественно, это приводит к возникновению трудностей при сравнении таблиц разного размера.
Отметим следующий немаловажный факт, очень редко рассматривающийся в ориентированной на социолога литературе.
Многие свойства рассматриваемых коэффициентов доказываются лишь при условии выполнения одного не всегда приемлемого для социологии предположения, состоящего в том, что за каждым нашим номинальным признаком "стоит" некая латентная (скрытая) непрерывная количественная (числовая) переменная.
Сделаем небольшое отступление по поводу используемых терминов. Все три определения к термину "переменная" требуют пояснения. Термин "латентная" употребляется здесь несколько условно. Обычно (в теории социологического измерения, например, в факторном, латентно-структурном анализе, многомерном шкалировании) под латентной переменной понимают признак, значения которого вообще не поддаются непосредственному измерению (например, путем прямого обращения к респонденту). Значения же нашей переменной мы измеряем самым непосредственным образом. Но получаем при этом номинальную шкалу, хотя и предполагаем, что между отвечающими этим значениям свойствами реальных объектов существуют отношения, достаточно сложные для того, чтобы можно было говорить об использовании интервальной шкалы (о соотношении между "богатством" реальных отношений между эмпирическими объектами и типом шкал, использующихся при шкалировании этих объектов, см., например [Клигер и др., 1978; Толстова, 1998]).
Термин "непрерывная" здесь употребляется в том смысле, что в качестве значения этой переменной может выступать любое рациональное число.
"Количественной" мы, в соответствии с традицией, называем переменную, значения которой получены по шкале, тип которой не ниже типа интервальной шкалы (о нашем отношении к подобному использованию терминов "качественный - количественный" уже шла речь в п.4.3 части I). Можно показать, что для таких шкал любое рациональное число может в принципе оказаться шкальным значением какого-либо объекта. Поэтому термины "количественный" и "непрерывный" часто употребляются как синонимы.)
Итак, мы полагаем, что каждый номинальный признак получен из некоторого количественного в результате произвольного разбиения диапазона его изменения на интервалы, количество которых равно числу значений нашей номинальной переменной. И, задавая респонденту интересующий нас вопрос в анкете, мы как бы принуждаем его разбить весь диапазон изменения рассматриваемой переменной на интервалы и указать, в каком из этих интервалов, по его мнению, находится оцениваемый объект. Внутри каждого интервала значения переменной становятся неразличимыми, между интервалами же определены лишь отношения совпадения – несовпадения (основное свойство номинальной шкалы). Когда исследователь имеет дело с двумя переменными такого рода (например, когда нас интересуют парные связи) то обычно предполагается еще и нормальность соответствующего двумерного распределения.
Именно таких предположений придерживался Пирсон, когда в начале века вводил свой коэффициент. Он доказал, что Р равно тому предельному значению обычного коэффициента корреляции между латентными переменными, к которому этот коэффициент стремится при безграничном увеличении количества градаций рассматриваемых признаков. Ясно, что без указанного предположения было бы совершенно неясно, как подобное свойство коэффициента Р можно проинтерпретировать.
Для исправления указанного недостатка коэффициента Пирсона (зависимости его максимально возможного значения от размеров таблицы сопряженности) Чупров ввел коэффициент Т, названный его именем. Но и Т достигает единицы лишь при c=r, и не достигает при c¹r. Может достигать единицы независимо от вида таблицы коэффициент Крамера К. Для квадратных таблиц коэффициенты Крамера и Чупрова совпадают, в остальных случаях К >Т.
Мы перечислили те свойства рассматриваемых коэффициентов, которые часто упоминаются в литературе. Из редко упоминающихся свойств можно упомянуть еще один свойственный всем коэффициентам недостаток – зависимость их величины от соотношений маргинальных частот анализируемой таблицы сопряженности (подчеркнем очень важный момент – вычисляя теоретические частоты, мы пользуемся маргинальными суммами, полагая, что имеем дело с их “генеральными” значениями, что, вообще говоря, не всегда отвечает реальности).
О том, как можно измерять связь между номинальными признаками с помощью критерия “Хи-квадрат”, можно прочесть в работах [Елисеева, 1982; Елисеева, Рукавишников, 1977, с.82-89; Интерпретация и анализ..., 1987, с.31-32; Лакутин, Толстова, 1990; Паниотто, Максименко, 1982, с.65-84; Рабочая книга социолога, 1983, с.169-172, 190 (с учетом того, что на с, 169 речь идет о таких теоретических частотах, которые являются частотами таблицы сопряженности, отвечающей случаю статистической независимости рассматриваемых номинальных переменных); Статистические методы..., 1979, с.117-120; Толстова, 1990а, с.54-57]
Перейдем к описанию таких коэффициентов парной связи, которые основаны на других априорных моделях, на другом понимании сути этой связи.






