ЗАДАНИЕ 1
Вычисление выражений в консольном приложении
Цель задания
1. Изучение порядка действий при вычислении выражений.
2. Получение навыков в записи выражений на языке C# и использовании стандартных методов.
Постановка задачи
1. Найти значение функции  при заданном
при заданном  (
( задается с клавиатуры). Используя стандартные функции вычислить целую часть числа
задается с клавиатуры). Используя стандартные функции вычислить целую часть числа  :
: 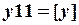 ; и округленное значение
; и округленное значение  :
:  (
( означает целую часть числа,
означает целую часть числа,  - округление до ближайшего целого).
- округление до ближайшего целого).
2. Записать выражение, зависящее от координат точки  , и принимающее значение True, если точка принадлежит заштрихованной области, и False в противном случае.
, и принимающее значение True, если точка принадлежит заштрихованной области, и False в противном случае.
3. Вывести результаты на экран и в файл.
Содержание отчета
1. Постановка задачи для конкретного варианта.
2. Текст программы.
3. Протокол выполнения программы.
4. Результаты вычислений.
Пример оформления отчета
Вариант 21, выполнил ст. гр. СТ-12 Иванов А.И.
1. Постановка задачи. Найти значение функции  при
при  , вычислить целую часть числа
, вычислить целую часть числа  :
: 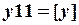 ; и округленное значение
; и округленное значение  :
:  , проверить принадлежность точки с координатами
, проверить принадлежность точки с координатами 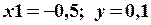 заданной области (рис. 0).
заданной области (рис. 0).

Текст программы.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
namespace ConsoleApplication_Lab1
{
class Program
{
static void Main(string[] args)
{
double x, y, x1, y1, y11, y22;
bool w;
Console.WriteLine("Введите x");
x = Convert.ToDouble(Console.ReadLine());
y = Math.Pow(2, -x) * Math.Sqrt(x + Math.Pow(Math.Abs(x), 1 / 3));
Console.WriteLine("При x={0} y={1}", x, y);
y11 = Math.Truncate(y);
y22 = Math.Round(y);
Console.WriteLine("При x={0} целая часть числа y=y11={1}", x, y11);
Console.WriteLine("При x={0} округленное значение y=y22={1}", x, y22);
Console.WriteLine("Введите x1");
x1 = Convert.ToDouble(Console.ReadLine());
Console.WriteLine("Введите y1");
y1 = Convert.ToDouble(Console.ReadLine());
// Выражение, описывающее попадание точки (x1,y1) в заданную область
w = x1 * x1 + y1 * y1 <= 1 &!(y1 < 0 & y1 > -x1);
Console.WriteLine("В точке x1={0}, y1={1} булевское значение величины w={2}", x1, y1, w);
Console.ReadLine();
FileStream s = new FileStream("rez.txt", FileMode.Create);
StreamWriter Wr = new StreamWriter(s);
Wr.WriteLine("При x={0} y={1}", x, y);
Wr.WriteLine("При x={0} целая часть числа y=y11={1}", x, y11);
Wr.WriteLine("При x={0} округленное значение y=y22={1}", x, y22);
Wr.WriteLine("В точке x1={0}, y1={1} булевское значение величины w={2}", x1, y1, w);
Wr.Close();
s.Close();
}
}
}
Протокол выполнения программы.

4. Результаты вычислений (содержимое файла “rez.txt”)
При x=1,5 y=0,559016994374947
При x=1,5 целая часть числа y=y11=0
При x=1,5 округленное значение y=y22=1
В точке x1=-0,5, y1=0,1 булевское значение величины w=True
________________________________________________________________
Функции y, значения x, x1, y1
Таблица 1.
 координаты
координаты  : 0.7; 0.7 : 0.7; 0.7
|
 координаты
координаты  : 1.7; 0.7 : 1.7; 0.7
|
 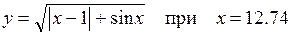 координаты
координаты  : 0.7; 0.2 : 0.7; 0.2
|
 координаты
координаты  : 0.2; 0.7 : 0.2; 0.7
|
 координаты
координаты  : -0.7; -0.7 : -0.7; -0.7 
|
 координаты
координаты  : 0.7; -0.9 : 0.7; -0.9
|
 координаты
координаты  : -0.3; -0.7 : -0.3; -0.7
|
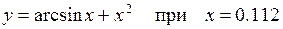 координаты
координаты  : 0.7; 0.7 : 0.7; 0.7
|
 координаты
координаты  : 0.7;-0.4 : 0.7;-0.4
|
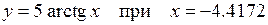 координаты
координаты  : 0.8; -0.7 : 0.8; -0.7
|
 координаты
координаты  : -0.7; 0.7 : -0.7; 0.7
|
 координаты
координаты  : 0.8; -0.3 : 0.8; -0.3
|






