ИНТЕГРИРОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ
ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ (ТРИГОНОМЕТРИЧЕСКИЕ,
ГИПЕРБОЛИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ)
| Вид интеграла | Метод интегрирования | |
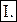 
| Универсальная тригонометрическая подстановка
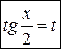 , ,  , тогда, , тогда,  , ,  , ,
 . .
| |
  ,
если ,
если  нечетная относительно нечетная относительно  : :

| Подстановка  , ,  тогда тогда
 , ,
 . .
| |
  ,
если ,
если  нечетная относительно нечетная относительно 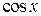 : :

| Подстановка  , ,  тогда тогда
 , ,
 . .
| |
  ,
если ,
если  четная относительно четная относительно 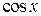 и и  : :

| Подстановка  , ,  тогда
тогда  , ,  , ,  . .
| |
  m и n – целые числа
m и n – целые числа
| 1) если m – нечетное положительное число, то подстановка  ;
2) если n – нечетное положительное
число, то подстановка ;
2) если n – нечетное положительное
число, то подстановка  ;
3) если m и n – четные неотрицательные числа, то для преобразования подынтегральной функции воспользоваться формулами ;
3) если m и n – четные неотрицательные числа, то для преобразования подынтегральной функции воспользоваться формулами
 , ,
 , ,
 ;
4) если m и n являются одновременно четными или нечетными и хотя бы один из них отрицателен, то подстановки ;
4) если m и n являются одновременно четными или нечетными и хотя бы один из них отрицателен, то подстановки  , , 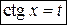 ;
5) если ;
5) если  четное отрицательное число, то подстановки четное отрицательное число, то подстановки  , , 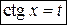 . .
| |
  , ,

| Подстановка  , ,  , ,  – дифференциальный бином. – дифференциальный бином.
|
| Вид интеграла | Метод интегрирования | |
  где m – целое положительное число
где m – целое положительное число
| Степень тангенса и котангенса последовательно понижается с помощью формул
 , ,
 . .
| |
  , ,
 ,
где n – четное положительное число. ,
где n – четное положительное число.
| Применить формулы
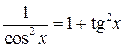 , ,
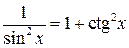 . .
| |
  , ,

| Интегралы от нечетной положительной степени секанса и косеканса проще всего находятся по рекрентным формулам, полученным методом интегрирования по частям


| |
  , ,
 , ,
 . .
| Применить формулы
 , ,
 , ,
 . .
| |
 
| Подстановка  или или  или или  для преобразования подынтегрального выражения использовать формулы
для преобразования подынтегрального выражения использовать формулы  , ,  , ,
 , ,  , ,
 , ,  , ,  , ,  , , 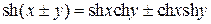 , ,  , , 
| |
 
| Подстановка  , , 
|
ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
| Вид интеграла | Метод интегрирования | |||
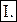
 R – рациональная функция,
R – рациональная функция,  , ,
 - дробно-рациональные числа, т.е. - дробно-рациональные числа, т.е.
 , ,  , …, , …,  . .
| Подстановка  , где s – общий знаменатель дробей , где s – общий знаменатель дробей  . .
| |||

 ,
R – рациональная функция, ,
R – рациональная функция,  , ,  , ,
 - дробно-рациональные числа, т.е. - дробно-рациональные числа, т.е.
 , ,  , …, , …,  . .
| Подстановка 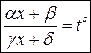 , где s – общий знаменатель дробей , где s – общий знаменатель дробей  . .
| |||
 1)
1)  ,
2) ,
2)  ,
3) ,
3)  . .
|
1)  или или  или или  ,
2) ,
2)  или или  или или  ,
3) ,
3) 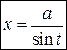 или или  или или
 . .
| |||


| Метод выделения полного квадрата, линейная подстановка
 
| |||


| 1) если  : первая подстановка Эйлера – : первая подстановка Эйлера –
 ;
2) если ;
2) если 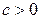 : вторая подстановка Эйлера – : вторая подстановка Эйлера –
 ;
3) если квадратный трехчлен имеет различные действительные корни х 1 и х 2,
т.е. ;
3) если квадратный трехчлен имеет различные действительные корни х 1 и х 2,
т.е.  : третья
подстановка Эйлера – : третья
подстановка Эйлера –  или
или  . .
| |||


| Интеграл вычисляется с помощью вспомогательного соотношения
 ,
где ,
где  - многочлен с неопределенными коэффициентами, постоянные - многочлен с неопределенными коэффициентами, постоянные  , ,  находятся дифференцированием вспомогательного соотношения с последующим применением метода сравнения коэффициентов при одинаковых степенях. находятся дифференцированием вспомогательного соотношения с последующим применением метода сравнения коэффициентов при одинаковых степенях.
| |||


| Интеграл сводится к интегралу вида  c помощью подстановки c помощью подстановки  . .
| |||

 , ,

| Подстановка 
| |||

 , ,

| 2-я подстановка Абеля 
| |||

 , ,
 , ,  - многочлен степени - многочлен степени 
| Разложить рациональную дробь  на простейшие, свести к интегралам VIII и IX. на простейшие, свести к интегралам VIII и IX.
| |||

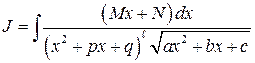

| 1) если квадратные трехчлены  и и  совпадают или отличаются множителем, то J представить в виде линейной комбинации интегралов совпадают или отличаются множителем, то J представить в виде линейной комбинации интегралов
 и и
 , для , для  – подстановка – подстановка  , для , для  – вторая подстановка Абеля – вторая подстановка Абеля  ; а) ; а)  подстановка подстановка  , где µ и ν подбираются так, чтобы в квадратных трехчленах исчезли члены с t в первой степени. б) , где µ и ν подбираются так, чтобы в квадратных трехчленах исчезли члены с t в первой степени. б)  подстановка подстановка  . .
| |||






