ќдной из важнейших задач статистики €вл€етс€ изучение изменений анализируемых показателей во времени, то есть их динамика. Ёта задача решаетс€ при помощи анализа р€дов динамики (временных р€дов).
–€д динамики Ц это числовые значени€ определенного статистического показател€ в последовательные моменты или периоды времени (т.е. расположенные в хронологическом пор€дке).
„исловые значени€ того или иного статистического показател€, составл€ющего р€д динамики, называют уровн€ми р€да и обычно обозначают через y. ѕервый член р€да y1 называют начальным (базисным) уровнем, а последний yn Ц конечным. ћоменты или периоды времени, к которым относ€тс€ уровни, обозначают через t.
–€ды динамики, как правило, представл€ют в виде таблицы (см. табл. 25) или графически (см. рис. 17)
“аблица 25. ¬нешнеторговый оборот (¬ќ) –оссии за период 2000-2006 гг.
| √од | |||||||
| ћлрд. долл. —Ўј | 149,9 | 155,6 | 168,3 | 212,0 | 280,6 | 368,9 | 468,4 |
–ис. 17. ¬нешнеторговый оборот (¬ќ) –оссии за период 2000-2006 гг.
ƒанные табл. 25 и рис. 17 нагл€дно иллюстрируют ежегодный рост внешнеторгового оборота (¬ќ) в –оссии за период 2000-2006 гг.
јнализ р€дов динамики начинаетс€ с определени€ того, как именно измен€ютс€ уровни р€да (увеличиваютс€, уменьшаютс€ или остаютс€ неизменными) в абсолютном и относительном выражении. „тобы проследить за направлением и размером изменений уровней во времени, дл€ р€дов динамики рассчитывают показатели изменени€ уровней р€да динамики:
Ц абсолютное изменение (абсолютный прирост);
Ц относительное изменение (темп роста или индекс динамики);
Ц темп изменени€ (темп прироста).
¬се эти показатели могут определ€тьс€ базисным способом, когда уровень данного периода сравниваетс€ с первым (базисным) периодом, либо цепным способом Ц когда сравниваютс€ два уровн€ соседних периодов.
јбсолютное изменение (абсолютный прирост) уровней рассчитываетс€ как разность между двум€ уровн€ми р€да по формуле (69) Ц дл€ базисного способа сравнени€ или по формуле (70) Ц дл€ цепного. ќно показывает, на сколько (в единицах показателей р€да) уровень одного (i -того) периода больше или меньше уровн€ какого-либо предшествующего периода, и, следовательно, может иметь знак Ђ+ї (при увеличении уровней) или ЂЦї (при уменьшении уровней).
 ; (69)
; (69)  . (70)
. (70)
¬ табл. 26 в столбце 3 рассчитаны базисные абсолютные изменени€ по формуле (69), а в столбце 4 Ц цепные абсолютные изменени€ по формуле (70).
“аблица 26. јнализ динамики ¬ќ –оссии
| √од | y | 
| 
| 
| 
| 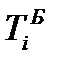 , % , %
| 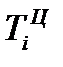 ,% ,%
|
| 149,9 | |||||||
| 155,6 | 5,7 | 5,7 | 1,038 | 1,038 | 3,8 | 3,8 | |
| 168,3 | 18,4 | 12,7 | 1,123 | 1,082 | 12,3 | 8,2 | |
| 212,0 | 62,1 | 43,7 | 1,414 | 1,260 | 41,4 | 26,0 | |
| 280,6 | 130,7 | 68,6 | 1,872 | 1,324 | 87,2 | 32,4 | |
| 368,9 | 219,0 | 88,3 | 2,461 | 1,315 | 146,1 | 31,5 | |
| 468,4 | 318,5 | 99,5 | 3,125 | 1,270 | 212,5 | 27,0 | |
| »того | 1803,7 | 318,5 | 3,125 |
ћежду базисными и цепными абсолютными изменени€ми существует взаимосв€зь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть
|
|
|
 . (71)
. (71)
¬ нашем примере про ¬ќ подтверждаетс€ правильность расчета абсолютных изменений по формуле (71): 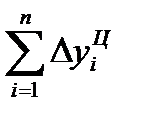 = 318,5 рассчитана в итоговой строке 4-го столбца, а
= 318,5 рассчитана в итоговой строке 4-го столбца, а  = 318,5 Ц в предпоследней строке 3-го столбца табл. 26.
= 318,5 Ц в предпоследней строке 3-го столбца табл. 26.
ќтносительное изменение (темп роста или индекс динамики) уровней рассчитываетс€ как отношение (деление) двух уровней р€да по формуле (72) Ц дл€ базисного способа сравнени€ или по формуле (73) Ц дл€ цепного.
 ; (72)
; (72)  . (73)
. (73)
ќтносительное изменение показывает во сколько раз уровень данного периода больше уровн€ какого-либо предшествующего периода (при 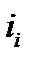 >1) или какую его часть составл€ет (при
>1) или какую его часть составл€ет (при 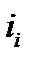 <1). ќтносительное изменение может выражатьс€ в виде коэффициентов, то есть простого кратного отношени€ (если база сравнени€ принимаетс€ за единицу), и в процентах (если база сравнени€ принимаетс€ за 100 единиц) путем домножени€ относительного изменени€ на 100%.
<1). ќтносительное изменение может выражатьс€ в виде коэффициентов, то есть простого кратного отношени€ (если база сравнени€ принимаетс€ за единицу), и в процентах (если база сравнени€ принимаетс€ за 100 единиц) путем домножени€ относительного изменени€ на 100%.
¬ табл. 26 в столбце 5 рассчитаны базисные относительные изменени€ по формуле (72), а в столбце 6 Ц цепные относительные изменени€ по формуле (73).
ћежду базисными и цепными относительными изменени€ми существует взаимосв€зь: произведение цепных относительных изменений равно последнему базисному изменению, то есть
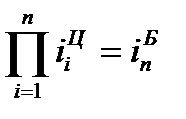 . (74)
. (74)
¬ нашем примере про ¬ќ подтверждаетс€ правильность расчета относительных изменений по формуле (74):  = 1,038*1,082*1,260*1,324*1,315*1,270 = 3,125 рассчитано по данным 6-го столбца, а
= 1,038*1,082*1,260*1,324*1,315*1,270 = 3,125 рассчитано по данным 6-го столбца, а  = 3,125 Ц в предпоследней строке 5-го столбца табл. 26.
= 3,125 Ц в предпоследней строке 5-го столбца табл. 26.
“емп изменени€ (темп прироста) уровней Ц относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнени€. ќн рассчитываетс€ путем вычитани€ из относительного изменени€ 100%, то есть по формуле (75):
 , (75)
, (75)
или как процентное отношение абсолютного изменени€ к тому уровню, по сравнению с которым рассчитано абсолютное изменение (базисный уровень), то есть по формуле (76):
 . (76)
. (76)
¬ табл. 26 в столбце 7 рассчитаны базисные темпы изменени€ ¬ќ по формуле (75), а в столбце 8 Ц цепные темпы изменени€ по формуле (76). ¬се расчеты в табл. 26 свидетельствуют о ежегодном росте ¬ќ –оссии за период 2000-2006 гг.
аждый р€д динамики можно рассматривать как некую совокупность n мен€ющихс€ во времени показателей, которые можно обобщить в виде средних величин. “акие обобщенные (средние) показатели особенно необходимы при сравнении динамики изменений того или иного показател€ ¬Ёƒ в разные периоды, в разных странах и т.д.
ќбобщенной характеристикой р€да динамики служит прежде всего средний уровень р€да 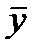 . ƒл€ разных видов р€дов динамики он рассчитываетс€ неодинаково. –€ды динамики бывают равномерные (с равными интервалами времени между уровн€ми), дл€ которых средний уровень определ€етс€ по простой формуле средней величины, и неравномерные (с неравными интервалами), дл€ которых используютс€ формулы средних взвешенных (по интервалам времени) величин. ¬ интервальном р€ду динамики (в котором врем€ задано в виде промежутков времени, к которым относ€тс€ уровни)
. ƒл€ разных видов р€дов динамики он рассчитываетс€ неодинаково. –€ды динамики бывают равномерные (с равными интервалами времени между уровн€ми), дл€ которых средний уровень определ€етс€ по простой формуле средней величины, и неравномерные (с неравными интервалами), дл€ которых используютс€ формулы средних взвешенных (по интервалам времени) величин. ¬ интервальном р€ду динамики (в котором врем€ задано в виде промежутков времени, к которым относ€тс€ уровни)  определ€етс€ по формуле средней арифметической, а в моментном р€ду (в котором врем€ задано в виде конкретных моментов времени или дат, к которым относ€тс€ уровни) Ц по формуле средней хронологической. ¬ табл. 27 привод€тс€ виды р€дов динамики и соответствующие формулы дл€ расчета их среднего уровн€
определ€етс€ по формуле средней арифметической, а в моментном р€ду (в котором врем€ задано в виде конкретных моментов времени или дат, к которым относ€тс€ уровни) Ц по формуле средней хронологической. ¬ табл. 27 привод€тс€ виды р€дов динамики и соответствующие формулы дл€ расчета их среднего уровн€  .
.
|
|
|
“аблица 27. ¬иды средних величин, примен€емых при расчете среднего уровн€
| ¬ид р€да динамики | Ќазвание средней величины | ‘ормула средней величины | Ќомер формулы |
| –авномерный интервальный | јрифметическа€ проста€ | 
| (77) |
| –авномерный моментный | ’ронологическа€ проста€ | 
| (78) |
| Ќеравномерный интервальный | јрифметическа€ взвешенна€ | 
| (79) |
| Ќеравномерный моментный | ’ронологическа€ взвешенна€ | 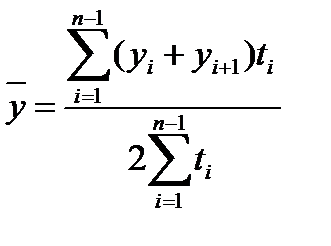
| (80) |
¬ нашем примере про ¬ќ –оссии за период 2000-2006 гг. имеем равномерный интервальный р€д динамики, поэтому его средний уровень определ€ем по формуле (77):  = 1803,7/7 = 257,671, то есть ¬ќ –оссии в период 2000-2006 гг. составл€л ежегодно в среднем 257,671 млрд. долл. —Ўј.
= 1803,7/7 = 257,671, то есть ¬ќ –оссии в период 2000-2006 гг. составл€л ежегодно в среднем 257,671 млрд. долл. —Ўј.
роме среднего уровн€ р€да рассчитываютс€ и другие средние показатели:
Ц среднее абсолютное изменение (средний абсолютный прирост);
Ц среднее относительное изменение (средний темп роста);
Ц средний темп изменени€ (средний темп прироста).
аждый из этих показателей может рассчитыватьс€ базисным и цепным способом.
Ѕазисное среднее абсолютное изменение Ц это частное от делени€ последнего базисного абсолютного изменени€ на количество изменений уровней (81); цепное среднее абсолютное изменение уровней р€да Ц это частное от делени€ суммы всех цепных абсолютных изменений на количество изменений (82):
 Ѕ =
Ѕ =  (81)
(81)  ÷ =
÷ =  (82)
(82)
ѕо знаку средних абсолютных изменений также суд€т о характере изменени€ €влени€ в среднем: рост, спад или стабильность. ќчевидно, что числители формулы (81) и (82) равны между собой по формуле (71), значит, среднее абсолютное изменение не зависит от способа расчета (базисный или цепной), так как результат получитс€ одинаковый. ¬ нашей задаче по формуле (81) или (82):
 = 318,5/6 = 53,083, то есть ежегодно в среднем ¬ќ растет на 53,083 млрд. долл.
= 318,5/6 = 53,083, то есть ежегодно в среднем ¬ќ растет на 53,083 млрд. долл.
Ќар€ду со средним абсолютным изменением рассчитываетс€ и среднее относительное. Ѕазисное среднее относительное изменение определ€етс€ по формуле (83), а цепное среднее относительное изменение Ц по формуле (84):
 Ѕ=
Ѕ=  =
=  (83)
(83)  ÷=
÷=  (84)
(84)
≈стественно, базисное и цепное среднее относительное изменени€ должны быть одинаковыми и сравнением их с критериальным значением 1 делаетс€ вывод о характере изменени€ €влени€ в среднем: рост, спад или стабильность. ¬ нашем примере про ¬ќ:  =
= 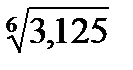 = 1,209, то есть ежегодно в среднем в период 2000-2006 гг. ¬ќ –оссии растет в 1,209 раза.
= 1,209, то есть ежегодно в среднем в период 2000-2006 гг. ¬ќ –оссии растет в 1,209 раза.
¬ычитанием 100% из среднего относительного изменени€ образуетс€ соответствующий средний темп изменени€, по знаку которого также можно судить о характере изменени€ изучаемого €влени€, отраженного данным р€дом динамики. ¬ нашем примере про ¬ќ:  = 1,209 Ц 1 = 0,209, то есть ежегодно в среднем в период 2000-2006 гг. ¬ќ –оссии растет на 20,9%.
= 1,209 Ц 1 = 0,209, то есть ежегодно в среднем в период 2000-2006 гг. ¬ќ –оссии растет на 20,9%.
ќдна из основных задач изучени€ р€дов динамики Ц вы€вить основную тенденцию (закономерность) в изменении уровней р€да, именуемую трендом. «акономерность в изменении уровней р€да в одних случа€х про€вл€етс€ нагл€дно, в других Ц может маскироватьс€ колебани€ми случайного или неслучайного характера. ѕоэтому, чтобы сделать правильные выводы о закономерност€х развити€ того или иного показател€, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. Ќа основании выделенного тренда можно экстраполировать (прогнозировать) развитие €влени€ в будущем. — этой целью (устранить колебани€, вызванные случайными причинами) р€ды динамики подвергают обработке.
—уществует несколько методов обработки р€дов динамики, помогающих вы€вить основную тенденцию изменени€ уровней р€да, а именно: метод укрупнени€ интервалов, метод скольз€щей средней и аналитическое выравнивание. ¬о всех методах вместо фактических уровней при обработке р€да рассчитываютс€ иные (расчетные) уровни, в которых тем или иным способом взаимопогашаетс€ действие случайных факторов и тем самым уменьшаетс€ колеблемость уровней. ѕоследние в результате станов€тс€ как бы Ђвыравненнымиї, Ђсглаженнымиї по отношению к исходным фактическим данным. “акие методы обработки р€дов динамики называютс€ сглаживанием или выравниванием р€дов динамики.
|
|
|
Ќаиболее совершенным методом обработки р€дов динамики в цел€х устранени€ случайных колебаний и вы€влени€ тренда €вл€етс€ выравнивание уровней р€да по аналитическим формулам (или аналитическое выравнивание). —уть аналитического выравнивани€ заключаетс€ в замене эмпирических (фактических, исходных) уровней yi теоретическими  , которые рассчитаны по определенному уравнению, прин€тому за математическую модель тренда, где теоретические уровни рассматриваютс€ как функци€ времени:
, которые рассчитаны по определенному уравнению, прин€тому за математическую модель тренда, где теоретические уровни рассматриваютс€ как функци€ времени:  = f(t).
= f(t).
ѕри этом каждый фактический уровень yi рассматриваетс€ как сумма двух[30] составл€ющих:
 , (85)
, (85)
где f(t) =  ≠ ≠- систематическа€ составл€юща€, отражающа€ тренд и выраженна€ определенным уравнением;
≠ ≠- систематическа€ составл€юща€, отражающа€ тренд и выраженна€ определенным уравнением;  - случайна€ величина, вызывающа€ колебани€ уровней вокруг тренда.
- случайна€ величина, вызывающа€ колебани€ уровней вокруг тренда.
«адача аналитического выравнивани€ сводитс€ к следующему:
1) определение на основе фактических данных формы (вида) гипотетической функции  = f(t), способной наиболее адекватно отразить тенденцию развити€ исследуемого показател€;
= f(t), способной наиболее адекватно отразить тенденцию развити€ исследуемого показател€;
2) нахождение по эмпирическим данным параметров указанной функции (уравнени€);
3) расчет по найденному уравнению теоретических (выравненных) уровней.
¬ аналитическом выравнивании наиболее часто используютс€ простейшие функции, представленные в табл. 28, где обозначено  - теоретические (выравненные) уровни (читаетс€ как Ђигрек, выравненный по tї); t Ц условное обозначение времени (1, 2, 3 Е); a0, a1, a2,... Ц параметры аналитической функции; k Ц число гармоник (при выравнивании по р€ду ‘урье).
- теоретические (выравненные) уровни (читаетс€ как Ђигрек, выравненный по tї); t Ц условное обозначение времени (1, 2, 3 Е); a0, a1, a2,... Ц параметры аналитической функции; k Ц число гармоник (при выравнивании по р€ду ‘урье).
¬ыбор той или иной функции дл€ выравнивани€ р€да динамики осуществл€етс€ на основании графического изображени€ эмпирических данных. ≈сли по тем или иным причинам уровни эмпирического р€да трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровн€ть каждую часть по соответствующей кривой.
“аблица 28. ¬иды математических функций[31], используемые при выравнивании
| Ќазвание функции | ¬ид функции | ‘ормула |
| ѕр€ма€ лини€ | 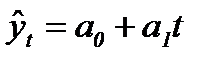 (86) (86)
| |
| ѕарабола 2-го пор€дка | или | 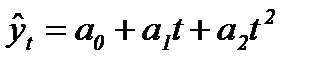 (87) (87)
|
| ѕарабола 3-го пор€дка |  (88) (88)
| |
| √ипербола |  (89) (89)
| |
| ѕоказательна€ |  (90) (90)
| |
| —тепенна€ | 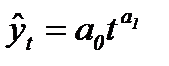 (91) (91)
| |
| –€д ‘урье |  (92) (92)
|
Ќередко один и тот же р€д можно выровн€ть по разным аналитическим функци€м и получить довольно близкие результаты. ¬ нашем примере про ¬ќ –оссии можно произвести выравнивание и по пр€мой линии, и по параболе. „тобы решить вопрос о том, использование какой кривой дает лучший результат, обычно сопоставл€ют суммы квадратов отклонений эмпирических уровней от теоретических (остатки), рассчитанным по разным функци€м, то есть:
 . (93)
. (93)
“а функци€, при которой эта сумма минимальна, считаетс€ наиболее адекватной, приемлемой. ќднако сравнивать непосредственно суммы квадратов отклонений можно в том случае, если сравниваемые уравнени€ имеют одинаковое число параметров. ≈сли же число параметров k разное, то каждую сумму квадратов дел€т на разность (n Ц k), выступающую в роли числа степеней свободы, и сравнивают уже квадраты отклонений уровней, рассчитанные на одну степень свободы (т.е. остаточные дисперсии на одну степень свободы).
ѕараметры искомых уравнений (a0, a1, a2,...) при аналитическом выравнивании могут быть определены по-разному, но наиболее распространенным методом €вл€етс€ метод наименьших квадратов (ћЌ ). ѕри этом методе учитываютс€ все эмпирические уровни и должна обеспечиватьс€ минимальна€ сумма квадратов отклонений эмпирических значений уровней y от теоретических уровней  :
:
|
|
|
 . (94)
. (94)
¬ частности, при выравнивании по пр€мой вида (86) параметры  и
и  отыскиваютс€ по ћЌ следующим образом. ¬ формуле (94) вместо
отыскиваютс€ по ћЌ следующим образом. ¬ формуле (94) вместо  записываем его конкретное выражение
записываем его конкретное выражение  . “огда
. “огда  . ƒальнейшее решение сводитс€ к задаче на экстремум, т.е. к определению того, при каком значении
. ƒальнейшее решение сводитс€ к задаче на экстремум, т.е. к определению того, при каком значении  и
и  функци€ двух переменных S может достигнуть минимума. ак известно, дл€ этого надо найти частные производные S по
функци€ двух переменных S может достигнуть минимума. ак известно, дл€ этого надо найти частные производные S по  и
и  , приравн€ть их к нулю и после элементарных преобразований решить систему двух уравнений с двум€ неизвестными.
, приравн€ть их к нулю и после элементарных преобразований решить систему двух уравнений с двум€ неизвестными.
¬ соответствии с вышеизложенным найдем частные производные:

—ократив каждое уравнение на 2, раскрыв скобки и перенес€ члены с y в правую сторону, а остальные Ц оставив в левой, получим систему нормальных уравнений:
 (95)
(95)
где n Ц количество уровней р€да; t Ц пор€дковый номер в условном обозначении периода или момента времени; y Ц уровни эмпирического р€да.
Ёта система и, соответственно, расчет параметров  и
и  упрощаютс€, если отсчет времени ведетс€ от середины р€да[32]. Ќапример, при нечетном числе уровней (как в нашем примере про ¬ќ –оссии Ц 7 уровней) серединна€ точка времени (год, мес€ц) принимаетс€ за нуль, тогда предшествующие периоды обозначаютс€ соответственно Ц1, Ц2, Ц3 и т.д., а следующие за средним (центральным) Ц соответственно 1, 2, 3 и т.д. (см. 3-й столбец табл. 29). ѕри четном числе уровней два серединных момента (периода) времени обозначают Ц1 и +1, а все последующие и предыдущие, соответственно, через два интервала:
упрощаютс€, если отсчет времени ведетс€ от середины р€да[32]. Ќапример, при нечетном числе уровней (как в нашем примере про ¬ќ –оссии Ц 7 уровней) серединна€ точка времени (год, мес€ц) принимаетс€ за нуль, тогда предшествующие периоды обозначаютс€ соответственно Ц1, Ц2, Ц3 и т.д., а следующие за средним (центральным) Ц соответственно 1, 2, 3 и т.д. (см. 3-й столбец табл. 29). ѕри четном числе уровней два серединных момента (периода) времени обозначают Ц1 и +1, а все последующие и предыдущие, соответственно, через два интервала:  ,
,  ,
,  и т.д.
и т.д.
ѕри таком пор€дке отсчета времени (от середины р€да)  = 0, поэтому, система нормальных уравнений (95) упрощаетс€ до следующих двух уравнений, каждое из которых решаетс€ самосто€тельно:
= 0, поэтому, система нормальных уравнений (95) упрощаетс€ до следующих двух уравнений, каждое из которых решаетс€ самосто€тельно:
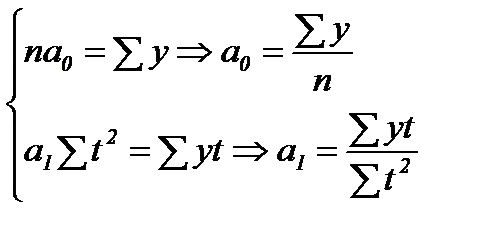 (96)
(96)
ак видим, при такой нумерации периодов параметр  представл€ет собой средний уровень равномерного интервального р€да, то есть формулу (77). ќпределим по формуле (96) параметры уравнени€ пр€мой дл€ нашего примера про ¬ќ –оссии, дл€ чего исходные данные и все расчеты необходимых сумм представим в табл. 29.
представл€ет собой средний уровень равномерного интервального р€да, то есть формулу (77). ќпределим по формуле (96) параметры уравнени€ пр€мой дл€ нашего примера про ¬ќ –оссии, дл€ чего исходные данные и все расчеты необходимых сумм представим в табл. 29.
“аблица 29. ¬спомогательные расчеты дл€ линейного тренда
| √од | Y | t | t2 | yt | 
| 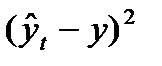
| 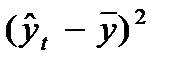
| 
|
| 439,0 | -3 | -1317,0 | 465,4 | 694,522 | 30571,200 | 40481,440 | ||
| 551,6 | -2 | -1103,2 | 523,6 | 781,712 | 13586,025 | 7849,960 | ||
| 734,9 | -1 | -734,9 | 581,9 | 23400,432 | 3395,626 | 8968,090 | ||
| 469,0 | 0,0 | 640,2 | 29314,615 | 0,000 | 29309,440 | |||
| 625,7 | 625,7 | 698,5 | 5300,164 | 3399,149 | 210,250 | |||
| 822,5 | 1645,0 | 756,8 | 4315,040 | 13593,073 | 33225,379 | |||
| 838,8 | 2516,5 | 815,1 | 564,113 | 30581,772 | 39452,884 | |||
| »того | 4481,5 | 1632,0 | 4481,5 | 64370,597 | 14755630,249 | 159497,442 |
»з табл. 29 получаем, что: a0 = 4481,5/7 = 640,2 и a1 = 1632,0/28 = 58,3. ќтсюда искомое уравнение тренда:  =640,2+58,3t. ¬ 6-м столбце табл. 29 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца Ц остатки по формуле (93). ƒл€ иллюстрации построим график эмпирических и трендовых уровней Ц рис. 18.
=640,2+58,3t. ¬ 6-м столбце табл. 29 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 7-го столбца Ц остатки по формуле (93). ƒл€ иллюстрации построим график эмпирических и трендовых уровней Ц рис. 18.
–ис. 18. Ёмпирические и трендовые уровни р€да динамики ¬ќ –оссии
ƒл€ найденного уравнени€ тренда необходимо провести оценку его надежности (адекватности), что осуществл€етс€ обычно с помощью критери€ ‘ишера, сравнива€ его расчетное значение Fр с теоретическим (табличным) значением F“ (ѕриложение 8). ѕри этом расчетный критерий ‘ишера определ€етс€ по формуле (97):
 , (97)
, (97)
где k Ц число параметров (членов) выбранного уравнени€ тренда.
ƒл€ проверки правильности расчета сумм в формуле (97) можно использовать следующее равенство (98):
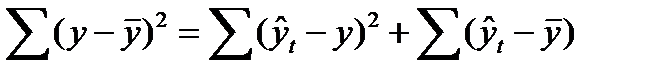 . (98)
. (98)
¬ нашем примере про ¬ќ равенство (98) соблюдаетс€ (необходимые суммы рассчитаны в трех последних столбцах табл. 29): 89410,434 = 9652,171 + 79758,263.
—равнение расчетного и теоретического значений критери€ ‘ишера ведетс€ при заданном уровне значимости[33]с учетом степеней свободы:  и
и  . ѕри условии Fр > F“ считаетс€, что выбранна€ математическа€ модель р€да динамики адекватно отражает обнаруженный в нем тренд.
. ѕри условии Fр > F“ считаетс€, что выбранна€ математическа€ модель р€да динамики адекватно отражает обнаруженный в нем тренд.
ѕроверим тренд на адекватность в нашем примере про ¬ќ по формуле (97):
F– = 79758,263*5/(9652,171*1) = 41,32 > F“, значит, модель адекватна и ее можно использовать дл€ прогнозировани€ (F“ = 6,61 находим по ѕриложению 8 в 1-ом столбце [  = k Ц 1 = 2 Ц 1 = 1] и 5-й строке [
= k Ц 1 = 2 Ц 1 = 1] и 5-й строке [  = n Ц k = 5]).
= n Ц k = 5]).
ак уже было отмечено ранее, в нашем примере про ¬ќ –оссии можно произвести выравнивание не только по пр€мой линии, но и по параболе, чего делать не будем, так как уже найденный линейный тренд адекватно описывает тенденцию[34].
|
|
|
ѕри составлении прогнозов уровней социально-экономических €влений обычно оперируют не точечной, а интервальной оценкой, рассчитыва€ так называемые доверительные интервалы прогноза. √раницы интервалов определ€ютс€ по формуле (99):
 , (99)
, (99)
где  Ц точечный прогноз, рассчитанный по модели тренда;
Ц точечный прогноз, рассчитанный по модели тренда; 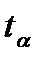 Ц коэффициент довери€ по распределению —тьюдента при уровне значимости
Ц коэффициент довери€ по распределению —тьюдента при уровне значимости 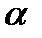 и числе степеней свободы
и числе степеней свободы  =nЦ1 (приложение 9)[35];
=nЦ1 (приложение 9)[35]; 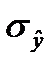 Ц ошибка аппроксимации, определ€ема€ по формуле (100):
Ц ошибка аппроксимации, определ€ема€ по формуле (100):
 . (100)
. (100)
—прогнозируем ¬ќ –оссии на 2007 и 2008 годы с веро€тностью 0,95 (значимостью 0,05), дл€ чего найдем ошибку аппроксимации по формуле (100): 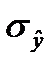 =
=  = 43,937 и найдем коэффициент довери€ по распределению —тьюдента по ѕриложению 9:
= 43,937 и найдем коэффициент довери€ по распределению —тьюдента по ѕриложению 9: 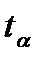 = 2,4469 при
= 2,4469 при  = 7 Ц 1= 6.
= 7 Ц 1= 6.
ѕрогноз на 2007 и 2008 годы с веро€тностью 0,95 по формуле (99):
Y2007 = (257,671+53,371 *4)  2,4469*43,937 или 363,6< Y2007 <578,7 (млрд. долл.);
2,4469*43,937 или 363,6< Y2007 <578,7 (млрд. долл.);
Y2008 = (257,671+53,371 *5)  2,4469*43,937 или 417,0< Y2008 <632,0 (млрд. долл.).
2,4469*43,937 или 417,0< Y2008 <632,0 (млрд. долл.).
ак видно из полученных прогнозов, доверительный интервал достаточно широк (из-за достаточно большой величины ошибки аппроксимации). Ѕолее точный прогноз можно получить при выравнивании по параболе 2-го пор€дка[36].
ћетодические указани€
ѕо данным ‘—√— сальдо внешней торговли (—¬“) –оссии за период 2000-2006 гг. характеризуетс€ р€дом динамики, представленным в табл. 30.
“аблица 30. —альдо внешней торговли (—¬“) –оссии за период 2000-2006 гг.
| √од | |||||||
| ћлрд. долл. —Ўј | 60,1 | 48,1 | 46,3 | 59,9 | 85,8 | 118,3 | 140,7 |
ѕроанализируем данный р€д динамики: вы€вим тенденцию и сделаем прогноз на 2007 и 2008 годы с веро€тностью 0,95.
ƒл€ большей нагл€дности представим данные табл. 30 на графике Ц рис. 19.
–ис. 19. —альдо внешней торговли (—¬“) –оссии за период 2000-2006 гг.
ƒанные табл. 30 и рис. 19 нагл€дно иллюстрируют постепенное уменьшение и последующий рост —¬“ –оссии за период 2000-2006 гг.. ќчевидно, что такую динамику не следует описывать линейной функцией тренда. ѕопробуем описать эту динамику с помощью тренда по параболе 2-го пор€дка по формуле (87). ѕараметры параболы (a0, a1, a2) определим методом ћЌ , дл€ чего в формуле (94) вместо  записываем выражение параболы
записываем выражение параболы  . “огда
. “огда 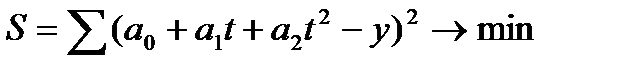 . ƒальнейшее решение сводитс€ к задаче на экстремум, т.е. к определению того, при каком значении a0, a1, a2 функци€ трех переменных S может достигнуть минимума. ак известно, дл€ этого надо найти частные производные S по a0, a1, a2 и приравн€ть их к нулю и после элементарных преобразований решить систему трех уравнений с трем€ неизвестными.
. ƒальнейшее решение сводитс€ к задаче на экстремум, т.е. к определению того, при каком значении a0, a1, a2 функци€ трех переменных S может достигнуть минимума. ак известно, дл€ этого надо найти частные производные S по a0, a1, a2 и приравн€ть их к нулю и после элементарных преобразований решить систему трех уравнений с трем€ неизвестными.
¬ соответствии с вышеизложенным найдем частные производные:

—ократив каждое уравнение на 2, раскрыв скобки и перенес€ члены с y в правую сторону, а остальные Ц оставив в левой, получим систему нормальных уравнений:
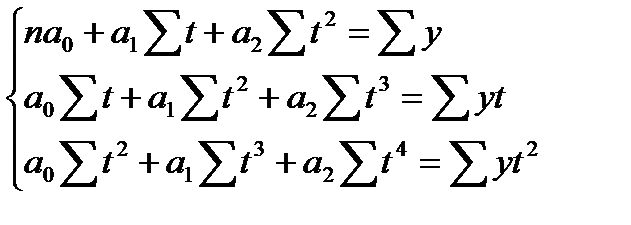 (101)
(101)
”простим систему (101), введ€ условную нумерацию t от середины р€да. “огда ∑ t = 0 и ∑ t3 = 0, а система (101) упроститс€ до следующего вида:
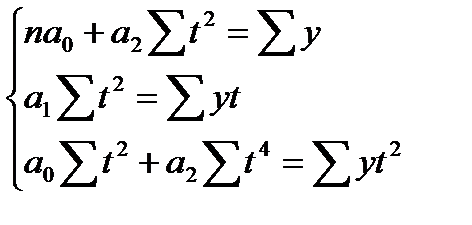 (102)
(102)
–еша€ систему (102) [37], находим параметры a0, a1, a2:
 (103)
(103)  (104)
(104)  (105)
(105)
ќпределим по формулам (103) Ц (105) параметры уравнени€ параболы дл€ нашего примера про —¬“ –оссии, дл€ чего исходные данные и все расчеты необходимых сумм представим в табл. 31.
“аблица 31. ¬спомогательные расчеты дл€ параболического тренда
| √од | y | t | t2 | t4 | yt | yt2 | 
| 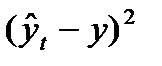
| 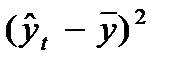
| 
|
| 60,1 | -3 | -180,3 | 540,9 | 56,614 | 12,150 | 1338,514 | 1095,610 | |||
| 48,1 | -2 | -96,2 | 192,4 | 49,764 | 2,770 | 1886,661 | 2034,010 | |||
| 46,3 | -1 | -46,3 | 46,3 | 51,679 | 28,929 | 1724,029 | 2199,610 | |||
| 59,9 | 0,0 | 0,0 | 62,357 | 6,038 | 951,282 | 1108,890 | ||||
| 85,8 | 85,8 | 85,8 | 81,800 | 16,000 | 129,960 | 54,760 | ||||
| 118,3 | 236,6 | 473,2 | 110,007 | 68,771 | 282,480 | 630,010 | ||||
| 140,7 | 422,1 | 1266,3 | 146,979 | 39,420 | 2892,135 | 2256,250 | ||||
| »того | 559,2 | 421,7 | 2604,9 | 559,200 | 174,079 | 9205,061 | 9379,140 |
»з табл. 31 получаем по формулам (103) Ц (105): a0 = 62,357, a1 = 15,061 и a2 = 4,382. ќтсюда искомое уравнение тренда  =62,357+15,061t+4,382t2. ¬ 8-м столбце табл. 31 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 9-го столбца Ц остатки по формуле (93). ƒл€ иллюстрации построим график эмпирических и трендовых уровней Ц рис. 20.
=62,357+15,061t+4,382t2. ¬ 8-м столбце табл. 31 приведены теоретические (трендовые) уровни, рассчитанные по этому уравнению, а в итоге 9-го столбца Ц остатки по формуле (93). ƒл€ иллюстрации построим график эмпирических и трендовых уровней Ц рис. 20.
–ис. 20. Ёмпирические и трендовые уровни —¬“ –оссии
јнализиру€ рис. 20, то есть сравнива€ эмпирические и теоретические уровни, отмечаем, что они почти полностью совпадают, значит парабола 2-го пор€дка Ц вполне адекватна€ функци€ дл€ отражени€ основной тенденции (тренда) —¬“ –оссии за 2000-2006 годы.
–авенство (98) соблюдаетс€ (необходимые суммы рассчитаны в трех последних столбцах табл. 31): 9379,140 = 174,079 + 9205,061. “еперь проверим тренд на адекватность по формуле (97): F– = 9205,061*4/(174,079*2) = 105,76 > F“, значит модель адекватна и ее можно использовать дл€ прогнозировани€ (F“ = 6,94 находим по ѕриложению 8 в 2-ом столбце [  = k Ц 1 = 3 Ц 1 = 2] и 4-й строке [
= k Ц 1 = 3 Ц 1 = 2] и 4-й строке [  = n Ц k = 4]).
= n Ц k = 4]).
—прогнозируем —¬“ –оссии на 2007 и 2008 годы с веро€тностью 0,95, дл€ чего найдем ошибку аппроксимации по формуле (100): 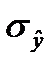 =
=  = 6,597 и найдем коэффициент довери€ по распределению —тьюдента по ѕриложению 9:
= 6,597 и найдем коэффициент довери€ по распределению —тьюдента по ѕриложению 9: 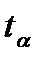 = 2,4469 при
= 2,4469 при  = 7 Ц 1= 6.
= 7 Ц 1= 6.
ѕрогноз —¬“ –оссии на 2007 и 2008 годы с веро€тностью 0,95 по формуле (99):
Y2007 = (62,357+15,061*4+4,382 *42)  2,4469*6,597 или 176,6< Y2007 <208,9 (млрд. долл.);
2,4469*6,597 или 176,6< Y2007 <208,9 (млрд. долл.);
Y2008 = (62,357+15,061*5+4,382 *52)  2,4469*6,597 или 231,1< Y2007 <263,4 (млрд. долл.).
2,4469*6,597 или 231,1< Y2007 <263,4 (млрд. долл.).
ак видно из полученных прогнозов, доверительный интервал достаточно узок, значит получен достаточно точный прогноз —¬“ –оссии на 2006 и 2007 годы. ≈го надежна€ оценка имеет принципиальное значение дл€ макроэкономического анализа и прогнозировани€, поскольку его величина вли€ет на общую картину платежного баланса. “ак, недооценка положительного сальдо означает недооценку отрицательного сальдо потоков капитала, и наоборот. ¬ то же врем€ потоки капитала ув€заны с динамикой внутренних сбережений, что имеет принципиально важное значение дл€ анализа инвестиционного потенциала и прогнозировани€ инвестиционной активности.
онтрольные задани€
ѕроанализировать динамику ¬Ёƒ –оссии за 12 мес€цев 2012 года и спрогнозировать ее на следующие 2 мес€ца по данным таблицы 32 (млн. долл. —Ўј).
“аблица 32. –аспределение вариантов дл€ выполнени€ контрольного задани€
| ћес€ц | ¬ариант | ||||||||
| Ёкспорт со странами дальнего зарубежь€ | »мпорт со странами дальнего зарубежь€ | Ёкспорт со странами —Ќ√ | »мпорт со странами —Ќ√ | —¬“ со странами дальнего зарубежь€ | —¬“ со странами —Ќ√ | ¬нешнеторговый оборот со всеми странами | Ёкспорт со всеми странами | »мпорт со всеми странами | —¬“ со всеми странами |
| €нварь | 34276,7 | 14895,5 | 5583,8 | 3129,7 | рассчитать самосто€тельно по исходным данным вариантов 1 Ц 4 | ||||
| февраль | 37827,0 | 20195,1 | 6693,5 | 3464,9 | |||||
| март | 39742,6 | 23232,1 | 7064,9 | 3936,4 | |||||
| апрель | 38377,5 | 21624,3 | 6216,0 | 3484,5 | |||||
| май | 38625,4 | 23005,7 | 6239,9 | 3489,4 | |||||
| июнь | 33970,7 | 22156,3 | 6427,6 | 3351,2 | |||||
| июль | 34221,5 | 24623,8 | 6712,6 | 3516,4 | |||||
| август | 33999,2 | 24530,1 | 6961,7 | 3639,7 | |||||
| сент€брь | 36153,1 | 22077,9 | 6864,8 | 3565,0 | |||||
| окт€брь | 39229,8 | 25970,7 | 7044,0 | 4691,6 | |||||
| но€брь | 38464,2 | 24565,3 | 6477,1 | 4338,0 | |||||
| декабрь | 40593,0 | 25406,1 | 6915,3 | 4242,8 |






