ѕризнаки, разрабатываемые таможенной статистикой внешней торговли, рассмотренные в предыдущей теме, варьируютс€ (отличаютс€ друг от друга) у различных единиц совокупности в один и тот же период или момент времени. Ќапример, величина внешнеторгового оборота варьируетс€ по подразделени€м ‘“—; величина экспорта (импорта) варьируетс€ по направлени€м экспорта (по разным странам-партнерам по внешней торговле), по видам товаров и т.п.
ѕричиной вариации €вл€ютс€ разные услови€ существовани€ разных единиц совокупности. Ќапример, огромное число причин вли€ет на масштабы внешней торговли различных стран мира.
ƒл€ управлени€ и изучени€ вариации статистикой разработаны специальные методы исследовани€ вариации, система показателей, с помощью которой вариаци€ измер€етс€, характеризуютс€ ее свойства.
ѕервым этапом статистического изучени€ вариации €вл€етс€ построение р€да распределени€ (или вариационного р€да) Ц упор€доченного распределени€ единиц совокупности по возрастающим (чаще) или по убывающим (реже) значени€м признака и подсчет числа единиц с тем или иным значением признака.
—уществует 3 вида р€да распределени€:
1) ранжированный р€д Ц это перечень отдельных единиц совокупности в пор€дке возрастани€ изучаемого признака (например, таблица 16); если численность единиц совокупности достаточно велика ранжированный р€д становитс€ громоздким, и в таких случа€х р€д распределени€ строитс€ с помощью группировки единиц совокупности по значени€м изучаемого признака (ели признак принимает небольшое число значений, то строитс€ дискретный р€д, а в противном случае Ц интервальный р€д);
2) дискретный р€д Ц это таблица, состо€ща€ из двух столбцов (строк) Ц конкретных значений варьирующего признака Xi и числа единиц совокупности с данным значением признака fi Ц частот; число групп в дискретном р€ду определ€етс€ числом реально существующих значений варьирующего признака;
3) интервальный р€д Ц это таблица, состо€ща€ из двух столбцов (строк) Ц интервалов варьирующего признака Xi и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа в общей численности совокупностей (частостей).
Ётап 1. ѕостроение ранжированного р€да распределени€. ѕостроим р€д распределени€ внешнеторгового оборота (¬ќ) по таможенным постам –оссии, дл€ чего необходимо провести статистическое наблюдение, то есть собрать первичный статистический материал, который представл€ет собой величину ¬ќ по всем таможенным постам, численность которых, как видно из рисунка 3, составл€ет 709 ед.
¬виду огромного массива данных применение сплошного наблюдени€ экономически нецелесообразно, поэтому в таких случа€х примен€етс€ выборочный метод, то есть из общего массива данных (генеральна€ совокупность) отбираетс€ некотора€ часть (выборочна€ совокупность, или выборка), котора€ и подвергаетс€ статистическому анализу. ѕри этом число единиц в выборке обозначают п, во всей генеральной совокупности Ц N. ќтношение n/N называетс€ относительный размер или частость выборки. ачество результатов выборочного метода зависит от репре≠зентативности выборки, т.е. от того, насколько она представительна в генеральной совокупности. ƒл€ обеспечени€ репрезентативности вы≠борки необходимо соблюдать принцип случайности отбора единиц.
|
|
|
¬ нашем примере про ¬ќ примем частость выборки n/N = 0,05 или 5%, то есть в выборку включим n = 0,05*709 = 35 таможенных постов из 709. –езультаты выборочного наблюдени€ ¬ќ по 35 таможенным постам за отчетный период представим в виде ранжированного по возрастанию величины ¬ќ р€да распределени€ (таблица 16).
“аблица 16. ¬нешнеторговый оборот (¬ќ) по 35 таможенным постам, млн.долл.
| є поста | ¬ќ | є поста | ¬ќ | є поста | ¬ќ |
| 24,16 | 54,12 | 65,31 | |||
| 27,06 | 54,91 | 69,24 | |||
| 29,12 | 55,74 | 71,39 | |||
| 31,17 | 55,91 | 77,12 | |||
| 37,08 | 56,07 | 79,12 | |||
| 39,11 | 56,80 | 84,34 | |||
| 41,58 | 56,93 | 86,89 | |||
| 44,84 | 57,07 | 91,74 | |||
| 46,80 | 58,39 | 96,01 | |||
| 48,37 | 59,61 | 106,84 | |||
| 51,44 | 59,95 | 111,16 | |||
| 52,56 | 62,05 | »того | 2100,00 |
”читыва€, что на основе выборочного обследовани€ нельз€ точно оценить изучаемый параметр (например, среднее значение Ц  или долю какого-то признака Ц d) генеральной совокупности, необходимо найти пределы, в которых он находитс€. ƒл€ этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю Ц
или долю какого-то признака Ц d) генеральной совокупности, необходимо найти пределы, в которых он находитс€. ƒл€ этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю Ц  и/или выборочную долю Ц
и/или выборочную долю Ц  ) и его дисперсию (
) и его дисперсию ( ).
).
¬ нашем примере про ¬ќ определим его средний размер в выборке по формуле (10), прин€в за X величину ¬ќ, а за N Ц численность выборки n:
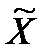 =
=  = 2100/35 = 60 (млн.долл.)
= 2100/35 = 60 (млн.долл.)
ƒисперсию (о ней будет рассказано чуть позднее Ц на 4-м этапе анализа вариации в этой теме) определим по формуле (46):
 =
=  = 445,778 (млн.долл.2)
= 445,778 (млн.долл.2)
«атем необходимо определить предельную ошибку выборки по формуле (32)[13]:
 = t
= t  , (32)
, (32)
где t Ц коэффициент довери€, завис€щий от веро€тности, с которой определ€етс€ предельна€ ошибка выборки;  Ц средн€€ ошибка выборки, определ€ема€ дл€ повторной выборки по формуле (33), а дл€ бесповторной Ц по формуле (34):
Ц средн€€ ошибка выборки, определ€ема€ дл€ повторной выборки по формуле (33), а дл€ бесповторной Ц по формуле (34):
 =
=  , (33)
, (33)  =
=  , (34)
, (34)
где n Ц численность выборки; N Ц численность генеральной совокупности.
¬ нашем примере про ¬ќ выборка бесповторна€, значит, примен€€ формулу (34), получим среднюю ошибку выборки при определении средней величины ¬ќ в генеральной совокупности:  =
= 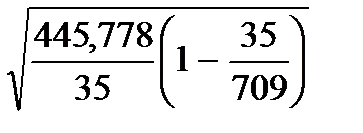 = 3,48 (млн.долл.).
= 3,48 (млн.долл.).
«начени€ веро€тности P и коэффициента довери€ t имеютс€ в таблицах нормального закона распределени€[14], из которых в статистике широко примен€ютс€ сочетани€ (если в выборке более 30 единиц), приведенные в таблице 17:
“аблица 17. Ќаиболее часто используемые значени€ интеграла веро€тностей Ћапласа
| P | 0,683 | 0,866 | 0,950 | 0,954 | 0,988 | 0,997 | 0,999 |
| t | 1,5 | 1,96 | 2,5 | 3,5 |
¬еро€тность, котора€ принимаетс€ при расчете выборочной характеристики, называетс€ доверительной. „аще всего принимают веро€тность P = 0,950 (t = 1,96), котора€ означает, что только в 5 случа€х из 100 ошибка может выйти за установленные границы.
ѕредельна€ ошибка выборки при определении средней величины ¬ќ по формуле (32):  = 1,96*3,48 = 6,82 (млн.долл.).
= 1,96*3,48 = 6,82 (млн.долл.).
ѕосле расчета предельной ошибки наход€т доверительный интервал обобщающей характеристики генеральной совокупности по формуле (35) Ц дл€ среднего значени€, и по формуле (36) Ц дл€ доли какого-либо признака:
|
|
|
 или (
или ( Ц
Ц  )
) 

 (
( +
+  )(35)
)(35)
 или (
или ( Ц
Ц  )
)  d
d  (
( +
+  )(36)
)(36)
¬ нашем примере про ¬ќ по формуле (35):
 = 60 ± 6,82 или 53,18
= 60 ± 6,82 или 53,18 

 66,82 (млн.долл.), то есть средн€€ величина ¬ќ в отчетном периоде по всем 709 таможенным постам с веро€тностью 0,95 лежит в пределах от 53,18 млн.долл. до 66,18 млн.долл.
66,82 (млн.долл.), то есть средн€€ величина ¬ќ в отчетном периоде по всем 709 таможенным постам с веро€тностью 0,95 лежит в пределах от 53,18 млн.долл. до 66,18 млн.долл.
Ётап 2. ѕостроение интервального р€да распределени€. ѕостроим интервальный р€д распределени€ ¬ќ по таможенным постам –оссии, дл€ чего необходимо выбрать оптимальное число групп (интервалов признака) и установить длину (размах) интервала. ѕоскольку при анализе р€да распределени€ сравнивают частоты в разных интервалах, необходимо, чтобы длина интервалов была посто€нной[15]. ќптимальное число групп выбираетс€ так, чтобы достаточной мере отразилось разнообразие значений признака в совокупности и в то же врем€ закономерность распределении, его форма не искажалась случайными колебани€ми частот. ≈сли групп будет слишком мало, не про€витс€ закономерность вариации; если групп будет чрезмерно много, случайные скачки частот исказ€т форму распределени€.
„аще всего число групп в р€ду распределени€ определ€ют по формуле —терждесса (37) или (38):
 (37) или
(37) или  ,(38)
,(38)
где k Ц число групп (округл€емое до ближайшего целого числа); N Ц численность совокупности.
»з формулы —терджесса видно, что число групп Ц функци€ объема данных (N).
«на€ число групп, рассчитывают длину (размах) интервала[16] по формуле (39):
 ,(39)
,(39)
где Xмax и Xmin Ч максимальное и минимальное значени€ в совокупности.
¬ нашем примере про ¬ќ по формуле —терждесса (37) определим число групп:
k = 1 + 3,322 lg 35 = 1+ 3,322*1,544 = 6,129 ≈ 6.
–ассчитаем длину (размах) интервала по формуле (39):
h = (111,16 Ц 24,16)/6 = 87/6 = 14,5 (млн.долл.).
“еперь построим интервальный р€д с 6 группами с интервалом 14,5 млн.долл. (см. первые 3 столбца табл. 18).
“аблица 18. »нтервальный р€д распределени€ ¬ќ по таможенным постам, млн.долл.
| i | √руппы постов по величине ¬ќ Xi | „исло постов fi | —ередина интервала ’ iТ | ’ iТ fi | Ќакопл. частота fiТ | | ’i Т -  | fi | fi
| (’i Т -  ) 2 fi ) 2 fi
| (’i Т -  ) 3 fi ) 3 fi
| (’i Т -  ) 4 fi ) 4 fi
|
| 24,16 Ц 38,66 | 31,41 | 157,05 | 147,071 | 4326,001 | -127246,23 | 3742856,97 | |||
| 38,66 Ц 53,16 | 45,91 | 321,37 | 104,400 | 1557,051 | -23222,31 | 346344,16 | |||
| 53,16 Ц 67,66 | 60,41 | 785,33 | 5,386 | 2,231 | -0,92 | 0,38 | |||
| 67,66 Ц 82,16 | 74,91 | 299,64 | 56,343 | 793,629 | 11178,84 | 157461,90 | |||
| 82,16 Ц 96,66 | 89,41 | 357,64 | 114,343 | 3268,572 | 93434,47 | 2670891,13 | |||
| 96,66 Ц 111,16 | 103,91 | 207,82 | 86,171 | 3712,758 | 159966,81 | 6892284,32 | |||
| »того | 2128,85 | 513,714 | 13660,243 | 114110,66 | 13809838,86 |
—ущественную помощь в анализе р€да распределени€ и его свойств оказывает графическое изображение. »нтервальный р€д изображаетс€ столбиковой диаграммой, в которой основани€ столбиков, расположенные по оси абсцисс, Ц это интервалы значений варьирующего признака, а высоты столбиков Ц частоты, соответствующие масштабу по оси ординат. √рафическое изображение распределени€ таможенных постов в выборке по величине ¬ќ приведено на рис. 8. ƒиаграмма такого типа называетс€ гистограммой [17].
–ис. 8. √истограмма распределени€ –ис. 9. ѕолигон распределени€
ƒанные табл. 18 и рис. 8 показывают характерную дл€ многих признаков форму распределени€: чаще встречаютс€ значени€ средних интервалов признака, реже Ц крайние (малые и большие) значени€ признака. ‘орма этого распределени€ близка к нормальному закону распределени€, которое образуетс€, если на варьирующую переменную вли€ет большое число факторов, ни один из которых не имеет преобладающего значени€.
|
|
|
≈сли имеетс€ дискретный р€д распределени€ или используютс€ середины интервалов (как в нашем примере про ¬ќ Ц в таблице 18 в 4-м столбце рассчитаны середины интервалов как полусумма значений начала и конца интервала), то графическое изображение такого р€да называетс€ полигоном (см. рис. 9)[18], которое получаетс€ соединением пр€мыми точек с координатами Xi и fi.
Ётап 3. –асчет структурных характеристик р€да распределени€. ѕри изучении вариации примен€ютс€ такие характеристики р€да распределени€, которые описывают количественно его структуру, строение. “акова, например, медиана Ц величина варьирующего признака, дел€ща€ совокупность на две равные части Ц со значением признака меньше медианы и со значением признака больше медианы[19]. ¬ нашем примере про ¬ќ (табл. 16) медиана Ц это 18-й таможенный пост из 35 с величиной ¬ќ 56,8 млн.долл. »з этого примера видно принципиальное различие между медианой и средней величиной: медиана не зависит от значений на кра€х ранжированного р€да. ƒаже если бы ¬ќ 35-го таможенного поста был в 10 раз больше, величина медианы не изменилась бы. ѕоэтому медиану часто используют как более надежный показатель типичного значени€ признака, нежели средн€€ арифметическа€, если р€д значений неоднороден, включает резкие отклонени€ от средней. ¬ интервальном р€ду распределени€ дл€ нахождени€ медианы примен€етс€ формула:
 , (40)
, (40)
где ће Ц медиана;
X0 Ц нижн€€ граница интервала, в котором находитс€ медиана;
h Ц величина (размах) интервала;
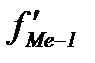 Ц накопленна€ частота в интервале, предшествующем медианному;
Ц накопленна€ частота в интервале, предшествующем медианному;
fMe Ц частота в медианном интервале.
¬ табл. 18 медианным €вл€етс€ среднее из 35 значений, т.е. 18-е от начала значение ¬ќ. ак видно из столбца накопленных частот (6-й столбец), оно находитс€ в третьем интервале. “огда по формуле (40):
 (млн.долл.).
(млн.долл.).
јналогично медиане вычисл€ютс€ значени€ признака, дел€щие совокупность на 4 равные по численности части Ц квартили, которые обозначаютс€ заглавной латинской буквой Q с подписным значком номера квартил€. ясно, что Q2 совпадает с ће. ƒл€ первого и третьего квартилей приводим формулы и расчет по данным табл. 18:
 (млн.долл.)
(млн.долл.)
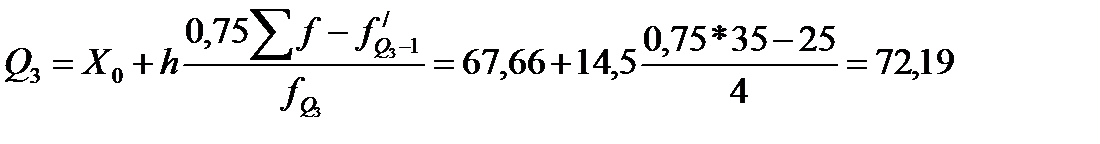 (млн.долл.)
(млн.долл.)
“ак как Q2 = ће = 59,30 млн.долл., видно, что различие между первым квартилем и медианой (Ц15,87) больше, чем между медианой и третьим квартилем (12,89). Ётот факт свидетельствует о наличии некоторой несимметричности в средней области распределени€, что заметно и на рис. 8.
«начени€ признака, дел€щие р€д на 5 равных частей, называютс€ квинтил€ми, на 10 частей Ц децил€ми, на 100 частей Ц перцентил€ми. Ёти характеристики примен€ютс€ при необходимости подробного изучени€ структуры р€да распределени€[20].
Ѕезусловно, важное значение имеет така€ величина признака, котора€ встречаетс€ в изучаемом р€ду распределени€ чаще всего. “акую величину прин€то называть модой. ¬ дискретном р€ду мода определ€етс€ без вычислени€ как значение признака с наибольшей частотой. ќбычно встречаютс€ р€ды с одним модальным значением признака. ≈сли в р€ду распределени€ встречаютс€ 2 или несколько равных (и даже несколько различных, но больших чем соседние) значений признака, то он считаетс€ соответственно бимодальным или мультимодальным. Ёто свидетельствует о неоднородности совокупности, возможно, представл€ющей собой агрегат нескольких совокупностей с разными модами. ¬ интервальном р€ду распределени€ интервал с наибольшей частотой €вл€етс€ модальным. ¬нутри этого интервала наход€т условное значение признака, вблизи которого плотность распределени€ (число единиц совокупности, приход€щихс€ на единицу измерени€ варьирующего признака) достигает максимума. Ёто условное значение и считаетс€ точечной модой. Ћогично предположить, что така€ точечна€ мода располагаетс€ ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. ќтсюда получаем обычно примен€емую формулу (41):
|
|
|
 , (41)
, (41)
где ћо Ц мода;
’0 Ц нижнее значение модального интервала;
fMo Ц частота в модальном интервале;
fMo-1 Ц частота в предыдущем интервале;
fMo+1 Ц частота в следующем интервале за модальным;
h Ц величина интервала.
ѕо данным табл. 18 рассчитаем точечную моду по формуле (41):
 (млн.долл.).
(млн.долл.).
изучению структуры р€да распределени€ средн€€ арифметическа€ величина также имеет отношение, хот€ основное значение этого обобщающего показател€ другое. ¬ интервальном р€ду распределени€ ¬ќ по таможенным постам средн€€ арифметическа€ рассчитываетс€ как взвешенна€ по частоте середина интервалов X (расчет числител€ Ц в 5-м столбце табл. 18) по формуле (11):
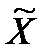 =
=  = 2128,85/35 = 60,82 (млн.долл.).
= 2128,85/35 = 60,82 (млн.долл.).
–азличие между средней арифметической величиной (60,82), медианой (59,30) и модой (58,96) в нашем примере невелико. „ем ближе распределение по форме к нормальному закону, тем ближе значени€ медианы, моды и средней величины между собой.
Ётап 4. –асчет показателей размера и интенсивности вариации. ѕростейшим показателем €вл€етс€ размах вариации Ц абсолютна€ разность между максимальным и минимальным значени€ми признака из имеющихс€ в изучаемой совокупности значений (42):
 . (42)
. (42)
ѕоскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измер€ть закономерную силу его вариации во всей совокупности. ѕредназначенный дл€ данной цели показатель должен учитывать и обобщать все различи€ значений признака в совокупности без исключени€. „исло таких различий равно числу сочетаний по два из всех единиц совокупности (в нашем примере про ¬ќ число сочетаний составит  ). ќднако нет необходимости рассматривать, вычисл€ть и осредн€ть все отклонени€. ѕроще использовать среднюю из отклонений отдельных значений признака от среднего арифметического значени€ признака, а таковых в нашем примере про ¬ќ всего 35. Ќо среднее отклонение значений признака от средней арифметической величины согласно первому свойству последней равно нулю. ѕоэтому показателем силы вариации выступает не арифметическа€ средн€€ отклонений, а средний модуль отклонений, или среднее линейное отклонение (43):
). ќднако нет необходимости рассматривать, вычисл€ть и осредн€ть все отклонени€. ѕроще использовать среднюю из отклонений отдельных значений признака от среднего арифметического значени€ признака, а таковых в нашем примере про ¬ќ всего 35. Ќо среднее отклонение значений признака от средней арифметической величины согласно первому свойству последней равно нулю. ѕоэтому показателем силы вариации выступает не арифметическа€ средн€€ отклонений, а средний модуль отклонений, или среднее линейное отклонение (43):
 . (43)
. (43)
¬ нашем примере про ¬ќ по данным табл. 18 среднее линейное отклонение вычисл€етс€ как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины (расчет числител€ произведен в 7-м столбце табл. 18), т.е. по формуле (44):
 (млн.долл.).(44)
(млн.долл.).(44)
Ёто означает, что в среднем величина ¬ќ в изучаемой совокупности таможенных постов отклон€лась от средней величины ¬ќ в –‘ на 14,678 млн.долл.
ѕростота расчета и интерпретации составл€ют положительные стороны показател€ Ћ, однако математические свойства модулей Ђплохиеї: их нельз€ поставить в соответствие с каким-либо веро€тностным законом, в том числе и с нормальным распределением, параметром которого €вл€етс€ не средний модуль отклонений, а среднее квадратическое отклонение, обозначаемое малой греческой буквой сигма ( ) или s и вычисл€емое по формуле (45) Ц дл€ ранжированного р€да и по формуле (46) Ц дл€ интервального р€да:
) или s и вычисл€емое по формуле (45) Ц дл€ ранжированного р€да и по формуле (46) Ц дл€ интервального р€да:
 ; (45)
; (45)  . (46)
. (46)
¬ нашем примере про ¬ќ по данным табл. 18 среднее квадратическое отклонение величины ¬ќ по формуле (46) составило (расчет числител€ произведен в 8-м столбце табл. 18):
 (млн.долл.).
(млн.долл.).
—реднее квадратическое отклонение по величине в реальных совокупност€х всегда больше среднего модул€ отклонений. –азница между ними тем больше, чем больше в изучаемой совокупности резких, выдел€ющихс€ отклонений, что служит индикатором Ђзасоренностиї совокупности неоднородными с основной массой элементами. ƒл€ нормального закона распределени€ отношение  . ¬ нашем примере про ¬ќ:
. ¬ нашем примере про ¬ќ: 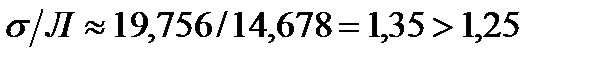 , т.е. в изучаемой совокупности наблюдаютс€ некоторое число таможенных постов с отличающимис€ от основной массы величинами ¬ќ.
, т.е. в изучаемой совокупности наблюдаютс€ некоторое число таможенных постов с отличающимис€ от основной массы величинами ¬ќ.
вадрат среднего квадратического отклонени€ представл€ет собой дисперсию отклонений, на использовании которой основаны практически все методы математической статистики, ее формула имеет вид (47) Ц дл€ несгруппированных данных (проста€ дисперси€) и (48) Ц дл€ сгруппированных (взвешенна€ дисперси€):
 ; (47)
; (47)  . (48)
. (48)
≈ще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в ее центральной части, служит среднее квартильное рассто€ние (отклонение), т.е. средн€€ величина разности между квартил€ми, определ€ема€ по формуле (49):
 . (49)
. (49)
¬ нашем примере про ¬ќ по формуле (49):  (млн.долл.).
(млн.долл.).
—ила вариации в центральной части совокупности, как правило, меньше, чем в целом по всей совокупности. —оотношение между средним линейным отклонением и средним квартильным рассто€нием служит дл€ изучени€ структуры вариации: большое значение такого соотношени€ свидетельствует о наличии слабоварьирующего Ђ€драї и сильно рассе€нного вокруг него окружени€ в изучаемой совокупности. ƒл€ нашего примера про ¬ќ соотношение Ћ/q = 1,021, что говорит о совсем незначительном различии силы вариации в центральной части совокупности и на ее периферии.
|
|
|
ƒл€ оценки интенсивности вариации и дл€ сравнени€ ее в разных совокупност€х и тем более дл€ разных признаков необходимы относительные показатели вариации, которые вычисл€ютс€ как отношение абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака, то есть показатели (50) Ц (53):
Ц относительный размах вариации:  ; (50)
; (50)
Ц линейный коэффициент вариации:  ; (51)
; (51)
Ц квадратический коэффициент вариации: 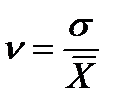 ; (52)
; (52)
Ц относительное квартильное рассто€ние:  .(53)
.(53)
¬ нашем примере про ¬ќ эти показатели составл€ют:
 = 87/60,82 =1,43, или 143%;
= 87/60,82 =1,43, или 143%;  = 14,678/60,82 = 0,241, или 24,1%;
= 14,678/60,82 = 0,241, или 24,1%;
 = 19,756/60,82 = 0,32, или 32%; d = 14,38/60,82 = 0,236, или 23,6%.
= 19,756/60,82 = 0,32, или 32%; d = 14,38/60,82 = 0,236, или 23,6%.
ќценка степени интенсивности вариации возможна только дл€ каждого отдельного признака и совокупности определенного состава, она состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив[21]. “ак, дл€ совокупности таможенных постов вариаци€ величины ¬ќ может быть определена как слаба€, если  < 25%, умеренна€ при 25% <
< 25%, умеренна€ при 25% <  < 50% и сильна€ при
< 50% и сильна€ при  > 50%.
> 50%.
–азлична€ сила, интенсивность вариации обусловлены объективными причинами, поэтому нельз€ говорить о каком-либо универсальном критерии вариации (например, 33%), так как дл€ разных €влений и признаков этот критерий различен[22].
Ётап 5. –асчет моментов распределени€ и показателей его формы. ƒл€ дальнейшего изучени€ характера вариации используютс€ средние значени€ разных степеней отклонений отдельных величин признака от его средней арифметической величины. Ёти показатели называютс€ центральные моменты распределени€ пор€дка, соответствующего степени, в которую возвод€тс€ отклонени€ (табл. 19) или просто моментов (нецентральные моменты в таможенной статистике практически не используютс€).
“аблица 19. ÷ентральные моменты
| ѕор€док момента | ‘ормула | |
| по несгруппированным данным | по сгруппированным данным | |
| ѕервый μ1 | 
| 
|
| ¬торой μ2 | 
| 
|
| “ретий μ3 | 
| 
|
| „етвертый μ4 | 
| 
|
¬еличина третьего момента μ3 зависит, как и его знак, от преобладани€ положительных кубов отклонений над отрицательными кубами либо наоборот. ѕри нормальном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов, поэтому на основе третьего момента строитс€ показатель, характеризующий степень асимметричности распределени€ Ц коэффициент асимметрии (54):
 . (54)
. (54)
¬ нашем примере про ¬ќ показатель асимметрии по формуле (54) составил (расчет числител€ произведен в 9-м столбце табл. 18):
 = 0,423 > 0, т.е. асимметри€ значительна.
= 0,423 > 0, т.е. асимметри€ значительна.
јнглийский статистик .ѕирсон на основе разности между средней арифметической величиной и модой предложил другой показатель асимметрии (55):
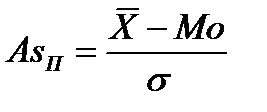 . (55)
. (55)
¬ нашем примере по данным табл. 18 показатель асимметрии по формуле (55) составил:  = 0,09.
= 0,09.
ѕоказатель асимметрии ѕирсона (55) зависит от степени асимметричности в средней части р€да распределени€, а показатель асимметрии (54) Ц от крайних значений признака. “аким образом, в нашем примере про ¬ќ в средней части распределени€ наблюдаетс€ меньша€ асимметри€, чем по кра€м, что видно и по графику (рис. 9). –аспределени€ с сильной правосторонней и левосторонней асимметрией показаны на рис. 10.
ћо 
|
 ћо ћо
|
| ѕравосторонн€€ As > 0 |
| Ћевосторонн€€ As < 0 |
–ис. 10. јсимметри€ распределени€
— помощью момента четвертого пор€дка характеризуетс€ еще более сложное свойство р€дов распределени€ Ц эксцесс (от англ. Ђизлишествої). ѕоказатель эксцесса рассчитываетс€ по формуле (56):
 . (56)
. (56)
„аще всего эксцесс интерпретируетс€ как Ђкрутизнаї распределени€, что не совсем верно. √рафик распределени€ может выгл€деть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариаци€, тем круче крива€ распределени€ при данном масштабе. Ќе говор€ уже о том, что, измен€€ масштабы по ос€м абсцисс и ординат, любое распределение можно искусственно сделать Ђкрутымї и Ђпологимї. „тобы показать, в чем состоит эксцесс распределени€, и правильно его интерпретировать, нужно сравнить р€ды с одинаковой силой вариации (одной и той же величиной σ) и разными показател€ми эксцесса. „тобы не смешать эксцесс с асимметрией, все сравниваемые р€ды должны быть симметричными. “акое сравнение изображено на рис. 11.
| Ex < 0 |
| Ќормальное распределение Ex = 0 |
| Ex > 0 |
–ис. 11. Ёксцесс распределени€
Ќаличие положительного эксцесса означает наличие слабоварьирующего Ђ€драї и сильно рассе€нного вокруг него окружени€ в изучаемой совокупности. ќтрицательный эксцесс означает отсутствие такого Ђ€драї.
¬ нашем примере по формуле (56) эксцесс составил (расчет числител€ произведен в 10-м столбце табл. 18):  , т.е. величина ¬ќ по таможенным постам варьирует сильнее, чем при нормальном распределении.
, т.е. величина ¬ќ по таможенным постам варьирует сильнее, чем при нормальном распределении.
ѕо значени€м показателей асимметрии и эксцесса распределени€ можно судить о близости распределени€ к нормальному: показатели асимметрии и эксцесса не должны превышать своих двукратных средних квадратических отклонений, т.е.  и
и  . Ёти средние квадратические отклонени€ вычисл€ютс€ по формулам (57) и (58):
. Ёти средние квадратические отклонени€ вычисл€ютс€ по формулам (57) и (58):
 ; (57)
; (57)  . (58)
. (58)
¬ нашем примере по формулам (57) и (58):


“ак как показатели асимметрии и эксцесса не превышают своих двухкратных средних квадратических отклонений (As = |0,423| < 0,4*2; Ex = |Ц0,41| < 0,78*2), можно говорить о сходстве анализируемого распределени€ с нормальным.
Ётап 6. ѕроверка соответстви€ р€да распределени€ теоретическому. ѕод теоретической кривой распределени€ понимаетс€ графическое изображение р€да в виде непрерывной линии изменени€ частот в вариационном р€ду, функционально св€занного с изменением вариантов, другими словами, теоретическое распределение может быть выражено аналитически Ц формулой, котора€ св€зывает частоты и соответствующие значени€ признака. “акие алгебраические формулы нос€т название законов распределени€. Ѕольшое познавательное значение имеет сопоставление фактических кривых распределени€ с теоретическими.
ак уже неоднократно отмечалось, часто пользуютс€ типом распределени€, которое называетс€ нормальным. ‘ормула функции плотности нормального распределени€ имеет следующий вид (59):
 или
или  (59)
(59)
где X Ц значение изучаемого признака;
 Ц средн€€ арифметическа€ р€да;
Ц средн€€ арифметическа€ р€да;
σ Ц среднее квадратическое отклонение;
 Ц нормированное отклонение;
Ц нормированное отклонение;
π = 3,1415 Ц посто€нное число (отношение длины окружности к ее диаметру);
e = 2,7182 Ц основание натурального логарифма.
—ледовательно, крива€ нормального распределени€ может быть построена по двум параметрам Ц средней арифметической и среднему квадратическому отклонению. ѕоэтому важно вы€снить, как эти параметры вли€ют на вид нормальной кривой.
≈сли  не мен€етс€, а измен€етс€ только σ, то чем меньше σ, тем более выт€нута вверх крива€ и наоборот, чем больше σ, тем более плоской и раст€нутой вдоль оси абсцисс становитс€ крива€ нормального распределени€ (см. рис. 12).
не мен€етс€, а измен€етс€ только σ, то чем меньше σ, тем более выт€нута вверх крива€ и наоборот, чем больше σ, тем более плоской и раст€нутой вдоль оси абсцисс становитс€ крива€ нормального распределени€ (см. рис. 12).
| X |
| f(X) |
| X |

|
| σ3 |
| σ2 |
| σ1 |
 = const
σ1 < σ2 < σ3 = const
σ1 < σ2 < σ3
|
–ис. 12. ¬ли€ние величины σ на кривую нормального распределени€
| f(X) |
 измен€етс€, то кривые нормального распределени€ имеют одинаковую форму, но отличаютс€ друг от друга положением максимальной ординаты (вершины) (см. рис. 13).
измен€етс€, то кривые нормального распределени€ имеют одинаковую форму, но отличаютс€ друг от друга положением максимальной ординаты (вершины) (см. рис. 13).

|

|

|
 < <  < < 
|
| σ = const |
–ис. 13. ¬ли€ние величины  на кривую нормального распределени€
на кривую нормального распределени€
»так, выделим особенности кривой нормального распределени€:
1) крива€ симметрична и имеет максимум в точке, соответствующей значению  = ће = ћо;
= ће = ћо;
2) кр ива€ асимптотически приближаетс€ к оси абсцисс, продолжа€сь в обе стороны до бесконечности (чем больше отдельные значени€ X отклон€ютс€ от  , тем реже они встречаютс€);
, тем реже они встречаютс€);
3) крива€ имеет две точки перегиба на рассто€нии ± σ от  ;
;
4) коэффициенты асимметрии и эксцесса равны нулю.
√ипотезы о распределени€х заключаютс€ в том, что выдвигаетс€ предположение о том, что распределение в изучаемой совокупности подчин€етс€ какому-то определенному закону. ѕроверка гипотезы состоит в том, чтобы на основании сравнени€ фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределени€ гипотетическому распределению.
ѕод гипотетическим распределением необ€зательно понимаетс€ нормальное распределение. ћожет быть выдвинута гипотеза о логнормальном, биномиальном распределени€х, распределении ѕуассона и пр.[23] ѕричина частого обращени€ к нормальному распределению состоит в том, что, как уже было замечено ранее, в этом типе распределени€ выражаетс€ закономерность, возникающа€ при взаимодействии множества случайных причин, когда ни одна из не имеет преобладающего вли€ни€.
¬ нашем примере про ¬ќ близость значений средней арифметической величины (60,82), медианы (59,30) и моды (58,96) указывает на веро€тное соответствие изучаемого распределени€ нормальному закону.
ѕроверка гипотезы о соответствии теоретическому распределению предполагает расчет теоретических частот этого распределени€.
ƒл€ нормального распределени€ пор€док расчета этих частот следующий:
1) по эмпирическим данным рассчитывают среднюю арифметическую р€да  и среднее квадратическое отклонение σ;
и среднее квадратическое отклонение σ;
2) наход€т нормированное (выраженное в σ) отклонение каждого эмпирического значени€ от средней арифметической:
 ;(60)
;(60)
3) по формуле (59) или с помощью таблиц интеграла веро€тностей Ћапласа наход€т значение φ (t)[24];
4) вычисл€ют теоретические частоты m по формуле:
 ,(61)
,(61)
где N Ц объем совокупности, hi Ц длина (размах) i -го интервала.
ќпределим теоретические частоты нормального распределени€ в нашем примере про ¬ќ по данным табл. 18, дл€ чего построим вспомогательную таблицу 20. —редн€€ арифметическа€ величина и среднее квадратическое отклонение нами уже найдены ранее ( ); значени€ нормированных отклонений t рассчитаны в 5-м столбце таблицы 20, а значени€ плотностей φ (t) Ц в 8-м столбце (в 6-м и 7-м столбцах приведены промежуточные расчеты по формуле (59)); в последнем столбце Ц теоретические частоты нормального распределени€.
); значени€ нормированных отклонений t рассчитаны в 5-м столбце таблицы 20, а значени€ плотностей φ (t) Ц в 8-м столбце (в 6-м и 7-м столбцах приведены промежуточные расчеты по формуле (59)); в последнем столбце Ц теоретические частоты нормального распределени€.
“аблица 20. –асчет теоретических частот нормального распределени€
| i | Xi | fi | ’iТ | 
| 
| 
| φ (t) | mi |
| 24,16 Ц 38,66 | 31,41 | -1,4889 | -1,1084 | 0,3301 | 0,0067 | 3,383 | ||
| 38,66 Ц 53,16 | 45,91 | -0,7549 | -0,2850 | 0,7520 | 0,0152 | 7,707 | ||
| 53,16 Ц 67,66 | 60,41 | -0,0210 | -0,0002 | 0,9998 | 0,0202 | 10,246 | ||
| 67,66 Ц 82,16 | 74,91 | 0,7130 | -0,2542 | 0,7756 | 0,0157 | 7,948 | ||
| 82,16 Ц 96,66 | 89,41 | 1,4470 | -1,0468 | 0,3510 | 0,0071 | 3,598 | ||
| 96,66 Ц 111,16 | 103,91 | 2,1809 | -2,3782 | 0,0927 | 0,0019 | 0,950 | ||
| »того | 33,832 |
—равним на графике эмпирические f (¬ќ по таможенным постам) и теоретические m (нормальное распределение) частоты, полученные на основе данных табл. 20 (рис. 14). Ѕлизость этих частот очевидна[25], но объективна€ оценка их соответстви€ может быть получена только с помощью критериев согласи€.
–ис. 14. –аспределение ¬ќ по таможенным постам (эмпирическое) и нормальное
ритерии согласи€, опира€сь на установленный закон распределени€, дают возможность установить, когда расхождени€ между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда Ц существенными (неслучайными). “аким образом, критерии согласи€ позвол€ют отвергнуть или подтвердить правильность выдвинутой гипотезы о характере распределени€ в эмпирическом р€ду и дать ответ, можно ли прин€ть дл€ данного эмпирического распределени€ модель, выраженную некоторым теоретическим законом распределени€.
—уществует р€д критериев согласи€, но чаще всего примен€ют критерии ѕирсона χ2, олмогорова и –омановского.
ритерий согласи€ ѕирсона χ2 (хи-квадрат) Ц один из основных критериев согласи€, рассчитываемый по формуле (62):
 , (62)
, (62)
где k Ц число интервалов;
fi Ц эмпирическа€ частота i -го интервала;
mi Ц теоретическа€ частота.
ƒл€ распределени€ χ2 составлены таблицы, где указано критическое значение критери€ согласи€ χ2 дл€ выбранного уровн€ значимости α и данного числа степеней свободы ν (см. ѕриложение 7).
”ровень значимости α Ц это веро€тность ошибочного отклонени€ выдвинутой гипотезы, т.е. веро€тность (P) того, что будет отвергнута правильна€ гипотеза. ¬ статистических исследовани€х в зависимости от важности и ответственности решаемых задач пользуютс€ следующими трем€ уровн€ми значимости:
1) α = 0,10, тогда P = 0,90;
2) α = 0,05, тогда P = 0,95 [26];
3) α = 0,01, тогда P = 0,99.
„исло степеней свободы ν определ€етс€ по формуле:
ν = k Ц z Ц 1,(63)
где k Ц число интервалов;
z Ц число параметров, задающих теоретический закон распределени€.
ƒл€ нормального распределени€ z = 2, так как нормальное распределение зависит от двух параметров Ц средней арифметической ( ) и среднего квадратического отклонени€ (σ).
) и среднего квадратического отклонени€ (σ).
ƒл€ оценки существенности расхождений расчетное значение χ2 сравнивают с табличным χ2 табл. –асчетное значени€ критери€ должно быть меньше табличного, т.е. χ2<χ2 табл, в противном случае расхождени€ между теоретическим и эмпирическим распределением не случайны, а теоретическое распределение не может служить моделью дл€ изучаемого эмпирического распределени€.
»спользование критери€ χ2 рекомендуетс€ дл€ достаточно больших совокупностей (N >50), при этом частота каждой группы не должна быть менее 5, в противном случае повышаетс€ веро€тность получени€ ошибочных выводов.
¬ нашем примере про ¬ќ дл€ расчета критери€ χ2 построим вспомогательную таблицу 21.
“аблица 21. ¬спомогательные расчеты критериев согласи€
| i | Xi | fi | mi | 
| fiТ | miТ | |fiТЦ miТ| |
| 24,16 Ц 38,66 | 3,383 | 0,773 | 3,383 | 1,617 | |||
| 38,66 Ц 53,16 | 7,707 | 0,065 | 11,090 | 0,910 | |||
| 53,16 Ц 67,66 | 10,246 | 0,740 | 21,336 | 3,664 | |||
| 67,66 Ц 82,16 | 7,948 | 1,961 | 29,284 | 0,284 | |||
| 82,16 Ц 96,66 | 3,598 | 0,045 | 32,882 | 0,118 | |||
| 96,66 Ц 111,16 | 0,950 | 1,160 | 33,832 | 1,168 | |||
| »того | 33,832 | 4,744 |
“еперь по формуле (62): χ2 =4,744, что меньше табличного (ѕриложение 7) значени€ χ2 табл=7,8147 при уровне значимости α = 0,05 и числе степеней свободы ν= 6Ц2Ц1=3, значит с веро€тностью 0,95 можно говорить, что в основе эмпирического распределени€ величины ¬ќ по таможенным постам лежит закон нормального распределени€, т.е. выдвинута€ гипотеза не отвергаетс€, а расхождени€ объ€сн€ютс€ случайными факторами.
ритерий –омановского – основан на использовании критери€ ѕирсона χ 2, т.е. уже найденных значений χ 2 и числа степеней свободы ν, рассчитываетс€ по формуле (64):
 . (64)
. (64)
ќн используетс€ в том случае, когда отсутствует таблица значений χ 2. ≈сли – < 3, то расхождени€ между теоретическим и эмпирическим распределением случайны, если – > 3, то не случайны, и теоретическое распределение не может служить моделью дл€ изучаемого эмпирического распределени€.
¬ нашем примере про ¬ќ по формуле (64):  = 0,712 < 3, что подтверждает несущественность расхождений между эмпирическими и теоретическими частотами.
= 0,712 < 3, что подтверждает несущественность расхождений между эмпирическими и теоретическими частотами.
ритерий олмогорова λ основан на определении максимального расхождени€ между накопленными частотами эмпирического и теоретического распределений (D), рассчитываетс€ по формуле (65) [27]:
 . (65)
. (65)
–ассчитав значение λ, по таблице P (λ) (см. ѕриложение 6) определ€ют веро€тность, с которой можно утверждать, что отклонени€ эмпирических частот от теоретических случайны. ¬еро€тность P (λ) может измен€тьс€ от 0 до 1. ѕри P (λ) = 1 (т.е. при λ < 0,3) происходит полное совпадение частот, при P (λ) = 0 Ц полное расхождение.
¬ нашем примере про ¬ќ в последних трех столбцах таблицы 21 приведены расчеты накопленных частот и разностей между ними, откуда видно, что в 3-ей группе наблюдаетс€ максимальное расхождение (разность) D = 3,664. “огда по формуле (65):  . ѕо таблице ѕриложени€ 6 находим значение веро€тности при λ = 0,6: P = 0,86 (наиболее близкое значение к 0,619), т.е. с веро€тностью, близкой к 0,86, можно говорить, что в основе эмпирического распределени€ величины ¬ќ по таможенным постам лежит закон нормального распределени€, а расхождени€ эмпирического и теоретического распределений нос€т случайный характер.
. ѕо таблице ѕриложени€ 6 находим значение веро€тности при λ = 0,6: P = 0,86 (наиболее близкое значение к 0,619), т.е. с веро€тностью, близкой к 0,86, можно говорить, что в основе эмпирического распределени€ величины ¬ќ по таможенным постам лежит закон нормального распределени€, а расхождени€ эмпирического и теоретического распределений нос€т случайный характер.
»так, подтвердив правильность выдвинутой гипотезы с помощью известных критериев согласи€, можно использовать результаты распределени€ дл€ практической де€тельности. акое же практическое значение может иметь произведенна€ проверка гипотезы? ¬о-первых, соответствие нормальному закону позвол€ет прогнозировать, какое число таможенных постов (или их дол€) попадет в тот или иной интервал значений величины ¬ќ. ¬о-вторых, нормальное распределение возникает при действии на вариацию изучаемого показател€ множества независимых факторов. »з чего следует, что нельз€ существенно снизить вариацию величины ¬ќ, воздейству€ только на один-два управл€емых фактора, скажем число работников таможенного поста или степень технической оснащенности.
ћетодические указани€
“аможенна€ инспекци€ провела 1%-ю проверку после выпуска товаров. ¬ результате получен следующий дискретный р€д распределени€ числа нарушений, вы€вленных в каждой проверке (табл. 22). ѕроведем анализ этого р€да распределени€.
“аблица 22. –€д распределени€ числа нарушений, вы€вленных таможенной инспекцией
| „исло нарушений | ||||
| „исло проверок |
Ётап 1. ƒанный в табл. 22 р€д распределени€ уже ранжирован в пор€дке возрастани€ числа нарушений, поэтому переходим сразу к расчету основного обобщающего показател€ Ц среднего числа нарушений. —начала рассчитаем среднее число нарушений в выборке, а также его дисперсию, дл€ чего построим вспомогательную таблицу 23.
“аблица 23. –€д распределени€ числа нарушений, вы€вленных таможенной инспекцией
| „исло нарушений X | „исло проверок f | Xf | (’-  ) 2 f ) 2 f
| m | 
| fТ | mТ | |fТЦ mТ| |
| 3,022 | 21,7 | 0,244 | 21,7 | 2,3 | ||||
| 1,665 | 7,7 | 1,778 | 29,4 | 1,4 | ||||
| 5,413 | 1,4 | 0,257 | 30,8 | 0,8 | ||||
| 6,997 | 0,2 | 3,200 | ||||||
| »того | 17,097 | 5,479 |
—реднее число нарушений в выборке по формуле (11), прин€в за X число нарушений, а за N Ц численность выборки n: 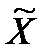 =
=  = 11/31 = 0,355 (нарушений).
= 11/31 = 0,355 (нарушений).
ƒисперсию определим по формуле (46):
 =
=  = 0,552 (нарушений2).
= 0,552 (нарушений2).
«атем определим среднюю ошибку выборки по формуле (33), так как число величин в генеральной совокупности N неизвестно:  =
=  .
.
ѕредельна€ ошибка выборки при веро€тности 0,95 по формуле (32):  = 1,96*0,133 = 0,261.
= 1,96*0,133 = 0,261.
ƒоверительный интервал среднего числа нарушений в генеральной совокупности по формуле (35):  = 0,355 ± 0,261 или 0,094
= 0,355 ± 0,261 или 0,094 

 0,616 (нарушений), то есть среднее число нарушений по всей совокупности товаров, прошедших через таможенную границу, с веро€тностью 0,95 лежит в пределах от 0,094 до 0,616 нарушений в 1 партии.
0,616 (нарушений), то есть среднее число нарушений по всей совокупности товаров, прошедших через таможенную границу, с веро€тностью 0,95 лежит в пределах от 0,094 до 0,616 нарушений в 1 партии.
Ќайдем еще обобщающий показатель Ц долю выпущенных товаров без нарушений d (т.е. с числом нарушений X =0). ƒол€ таких товаров в выборке по формуле (6) составила: 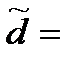 24/31 = 0,774, или 77,4%.
24/31 = 0,774, или 77,4%.
ƒисперси€ этой доли по формуле (66) [28] составила:
 = 0,774*(1Ц0,774) = 0,175. (66)
= 0,774*(1Ц0,774) = 0,175. (66)
—редн€€ ошибка выборки по формуле (33):  =
=  .
.
ѕредельна€ ошибка выборки при веро€тности 0,95 по формуле (32):  = 1,96*0,075 = 0,147.
= 1,96*0,075 = 0,147.
ƒоверительный интервал доли выпущенных товаров без нарушений в генеральной совокупности по формуле (36): d = 0,774 ± 0,147 или 0,627  d
d  0,921, то есть дол€ выпущенных товаров без нарушений по всей совокупности товаров, прошедших через таможенную границу, с веро€тностью 0,95 лежит в пределах от 62,7% до 92,1%.
0,921, то есть дол€ выпущенных товаров без нарушений по всей совокупности товаров, прошедших через таможенную границу, с веро€тностью 0,95 лежит в пределах от 62,7% до 92,1%.
Ётап 2. ƒанный р€д распределени€ не имеет смысла превращать в интервальный в виду очень малой вариации значений признака. ѕостроив график этого распределени€ (полигон) Ц рис. 15, видно, что данное распределение не похоже на нормальное.
–ис. 15. рива€ распределени€ числа нарушений, вы€вленных таможенной инспекцией
Ётап 3. »з структурных характеристик р€да распределени€ можно определить только моду: ћо = 0, так как по данным табл. 23 такое число нарушений чаще всего встречаетс€ (f =24).
Ётап 4. ѕо формуле (42) определим размах вариации: H = 3 Ц 0 = 3, что характеризует вариацию в 3 нарушени€.
ѕо формуле (44) найдем среднее линейное отклонение:
 .
.
Ёто означает, что в среднем число нарушений в выборке отклон€етс€ от среднего числа нарушений на 0,55.
—реднее квадратическое отклонение рассчитаем не по формуле (46), а как корень из дисперсии, котора€ уже была рассчитана нами на 1-м этапе:  , тогда
, тогда 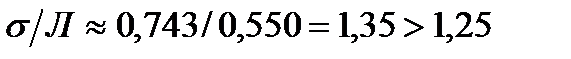 , т.е. в изучаемом распределении наблюдаетс€ некоторое число выдел€ющихс€ нарушений (с большим числом нарушений, вы€вленных в одной проверке).
, т.е. в изучаемом распределении наблюдаетс€ некоторое число выдел€ющихс€ нарушений (с большим числом нарушений, вы€вленных в одной проверке).
ѕоскольку кварт






