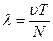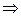Свириденко О.Ф
Механічні
коливання і хвилі
навчальний посібник
з курсу фізики
для студентів І курсу

2012
У навчальному посібнику викладено матеріал з фізики з розділу «Механічні коливання і хвилі», який входить до модуля № 4. Посібник містить теоретичний матеріал у систематизованому вигляді, а також приклади типових задач та завдання для самостійного розв’язування по означеній темі.
Даний навчальний посібник призначений для студентів І курсу технікумів, коледжів, училищ, а також може бути використаний учнями 11 класу і викладачами фізики середніх навчальних закладів освіти.
Тема 1. Механічні коливання
1.1. Загальні поняття
Коливаннями називають такі зміни стану системи, які періодично повторюються в часі. Наприклад: механічні коливання тіла на пружині, коливання маятників, коливання струн, вібрації фундаментів будівель; електромагнітні коливання в коливальному контурі, змінний струм; коливання мембрани телефона, дифузора гучномовця.
Коливальна система – система, в якій одне або декілька тіл можуть здійснювати коливання.
Коливальна точка (тіло) – точка (тіло), що здійснює коливання.
Повне коливання – один закінчений цикл коливального руху, після якого він повторюється у тому самому порядку.
1.2. Класифікація коливань за:
1) фізичною природою – механічні, електромагнітні, електромеханічні.
2) характером – власні, вільні, вимушені, автоколивання.
Хоча коливання досить різноманітні за своєю фізичною природою, але вони мають спільні закономірності й описуються однотипними математичними методами.
Механічні коливання – періодично повторюваний рух коливальної системи по якій-небудь траєкторії, яку ця система проходить по черзі у протилежних напрямах відносно положення рівноваги.
Електромагнітні коливання – періодичні зміни заряду та характеристик електричного і магнітного полів.
Умови виникнення коливань
1. Наявність у точки надлишкової енергії, порівняно з її енергією у положенні стійкої рівноваги.
2. Надлишкова енергія, набута точкою внаслідок виведення її з положення рівноваги не повинна повністю витрачатися на подолання опору середовища під час повернення в це положення.
3. Дія на точку повертальної сили, що виникає при виведенні її з положення рівноваги і завжди до нього напрямленої.
1.4.Класифікація коливань залежно від сил, що діють на
Коливну точку
1. Власні – здійснюються під дією тільки повертальної сили (можливі тільки у вакуумі).
2. Вільні – здійснюються під дією повертальної сили і сили опору середовища (реальні коливання, затухаючі)
3. Вимушені – здійснюються під дією повертальної сили, сили опору середовища і зовнішньої періодично діючої сили; характер коливань залежить від співвідношення цих сил.
Параметри коливань
1. Період Т (с) – характеризує періодичність коливань і вимірюється часом, затраченим на одне повне коливання тобто мінімальний проміжок часу, через який повторюється певне значення змінної величини, що характеризує коливальну систему.
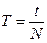
2. Частота ν (Гц) – характеризує швидкість повторюваності коливань і вимірюється кількістю коливань, здійснених коливальною системою за одиницю часу.

3. Циклічна частота ω (рад/с) – вимірюється кількістю коливань, здійснених коливальною системою за 2π одиниць часу.

4. Амплітуда А – максимальне значення величини, що характеризує миттєвий стан коливальної системи; А > 0
А (t) = const – коливання незатухаючі;
А (t)↓ – коливання затухаючі.
1.6.Характеристики миттєвого стану механічних коливань
Точки
1. Зміщеннях (м) – характеризує положення коливальної точки в даний момент часу і дорівнює відстані точки від положення стійкої
рівноваги до її положення в даний момент часу.
2. Швидкість υ (м/с) – характеризує швидкість зміни положення коливальної точки і дорівнює похідній зміщення за часом.

3. Прискорення а (м/с2) – характеризує бистроту зміни швидкості коливальної точки і дорівнює похідній швидкості за часом або другій похідній зміщення за часом.

4. Фаза φ (1; рад) – визначає стан коливальної системи при заданій амплітуді в довільний проміжок часу, тобто характеризує положення і напрям руху коливальної точки в даний момент часу і показує, яка частина періоду пройшла від початку коливань.
φ = ωt + φ0
φ0 – початкова фаза – показує, на якому етапі знаходився коливальний рух у момент початку відліку часу.
Фаза не пов’язана з амплітудою коливань на відміну від зміщення.
Зміна фази під час коливань маятника

Співвідношення фази у різних одиницях вимірювання
з частинами періоду

|

| |
| Час | Фаза, 1 | Фаза, рад |
| t = 0 | ||

| 
| 
|

| 
| 
|

| 
| 
|

| φ = 1 | 
|
Коли два коливання відбуваються з однаковим періодом (частотою), то різниця фаз між ними зберігається сталою протягом усього часу коливань.
| Синфазні коливання (однакові фази) | Протифазні коливання (протилежні фази) | |||
| Т1 = Т2, А1 = А2 Напрями коливань однакові Δφ = φ1 – φ2 = 0 або 1 (Δφ = 2nπ) | Т1 = Т2, А1 = А2 Напрями коливань протилежні Δφ = φ – φ = ½ (Δφ = (2n+1)π) | |||

| 
|
1.7. Гармонічні коливання
1.7.1. Гармонічні коливання – коливання, під час яких характеристики миттєвого стану коливальної системи змінюються з плином часу за законом синуса або косинуса.
| Зміщення | x = хmaх cos(ωt + φ0) | x(t) = хmaх sin(ωt + φ0) | |
| Швидкість | υ(t) = – ωхmaх sin(ωt + φ0) = = – υmaх sin(ωt + φ0) | υ(t) = ω хmaх cos(ωt + φ0) = = υmaх cos(ωt + φ0) | |
| Амплітуда швидкості | υmaх = ωхmaх | ||
| Прискорення | a(t) = – ωυmaх cos(ωt + φ0) = = – amaxcos(ωt + φ0) | a(t)= – ωυmaхsin(ωt + φ0) = = – amaxsin(ωt + φ0) | |
| Амплітуда прискорення | amax = ωυmaх = ω2хmaх | ||
| Диференціальне рівняння |  або x" + ω2x = 0 або x" + ω2x = 0
| ||
| Фаза | 
| ||
| Повертальна сила | Fп ~ – k x | ||
1.7.2. Графіки гармонічних коливань
Графіки коливань х(t), υ(t), a(t)
|

Графіки коливань х(φ), υ(φ), a(φ), [φ = ωt]


1.7.3. Геометрична інтерпретація гармонічних коливань
 Гармонічне коливання можна подати як коливання вздовж осі Ох проекції кінця радіус-вектора точки, що рухається по колу радіусом А. Якщо в момент часу t0 = 0 радіус вектор ОВ утворює з віссю Оу кут φ0, а за час t описує кут ωt, так що в довільний момент часу x = Asin(ωt + φ0), де А = хmaх.
Гармонічне коливання можна подати як коливання вздовж осі Ох проекції кінця радіус-вектора точки, що рухається по колу радіусом А. Якщо в момент часу t0 = 0 радіус вектор ОВ утворює з віссю Оу кут φ0, а за час t описує кут ωt, так що в довільний момент часу x = Asin(ωt + φ0), де А = хmaх.
1.8. Вільні коливання
 У реальних коливальних системах за рахунок зміни енергії коливального руху виконується робота проти сил тертя й опору. Тому з часом амплітуда вільних коливань зменшується, а їх період збільшується – коливання затухають.
У реальних коливальних системах за рахунок зміни енергії коливального руху виконується робота проти сил тертя й опору. Тому з часом амплітуда вільних коливань зменшується, а їх період збільшується – коливання затухають.
Інколи цей процес посилюють за допомогою спеціальних пристроїв. Наприклад, у транспортних засобах використовують різні амортизатори, які гасять коливання кузова, зумовлені нерівностями дороги.
1.9. Вимушені коливання. Явище резонансу
Для того, щоб коливання в системі не затухали, необхідно компенсувати втрати енергії, спричинені дією сили тертя і опору. Енергію в системі треба поповнювати періодично. Це досягається періодичною дією на систему зовнішньої сили.
Коливання системи, які виникають під дією зовнішньої періодично змінної сили, називаються вимушеними.
Зі зміною частоти ω зовнішньої сили змінюються амплітуди вимушених коливань. Якщо ця частота наближається до частоти вільних коливань системи ω0, то амплітуда вимушених коливань збільшується, досягаючи максимуму. Зі збільшенням частоти (ω > ω0) амплітуда вимушених коливань зменшується.
 Явище різкого зростання амплітуди вимушених коливань у разі наближення частоти дії зовнішньої періодичної сили до частоти вільних коливань системи називають резонансом. Графік залежності амплітуди коливань від частоти під час резонансу називається резонансною кривою Резонансна крива тим гостріша, чим менші втрати енергії в системі. Ці втрати можуть бути зумовлені внутрішнім тертям середовища, тобто чим менший коефіцієнт в’язкості (внутрішнього тертя) середовища, тим яскравіше проявляється резонанс (тим гостріше резонансна крива) (див. рис).
Явище різкого зростання амплітуди вимушених коливань у разі наближення частоти дії зовнішньої періодичної сили до частоти вільних коливань системи називають резонансом. Графік залежності амплітуди коливань від частоти під час резонансу називається резонансною кривою Резонансна крива тим гостріша, чим менші втрати енергії в системі. Ці втрати можуть бути зумовлені внутрішнім тертям середовища, тобто чим менший коефіцієнт в’язкості (внутрішнього тертя) середовища, тим яскравіше проявляється резонанс (тим гостріше резонансна крива) (див. рис).
Явище резонансу може бути корисним, оскільки воно дає змогу навіть за допомогою малої сили суттєво збільшити амплітуду, наприклад, укладання бетону за допомогою вібраторів.
Резонанс може бути шкідливим і небезпечним. З метою запобігання цьому слід заздалегідь обчислювати частоти коливань різних машин, засобів транспорту, фундаментів тощо, щоб у звичайних умовах їх експлуатації не міг настати резонанс.
У повсякденному житті можна спостерігати, як в кімнаті бряжчать шибки під час проходження по вулиці важкого вантажного автомобіля. Це означає, що власні частоти коливань шибок дорівнюють частоті коливань деталей автомобіля.
Автоколивання
Автоколивання – незатухаючі коливання, які здійснюються за рахунок внутрішніх джерел енергії.
Схема автоколивальної системи

Зворотній зв’язок
 Приклади автоколивальних систем:
Приклади автоколивальних систем:
1. Годинниковий механізм з маятником (рис.)
1 – гиря (джерело енергії),
2 – ходове колесо (регулюючий пристрій),
3 – анкер (здійснює зворотній зв’язок),
4 – маятник (коливальна система).
2. Серцево-судинна система людини.
3. Людина, що катається на гойдалці.
4. ДВЗ.
5. Голосові зв’язки під час розмови.
Приклади розв’язування задач

 Задача 2. За графіком х (t) визначити 1) амплітуду зміщення; 2) період; 3) початкову фазу; 4) частоту; 5) циклічну частоту; 6) амплітуду швидкості; 7) амплітуду прискорення; 8) рівняння зміни зміщення; 9) рівняння зміни швидкості; 10) рівняння зміни прискорення.
Задача 2. За графіком х (t) визначити 1) амплітуду зміщення; 2) період; 3) початкову фазу; 4) частоту; 5) циклічну частоту; 6) амплітуду швидкості; 7) амплітуду прискорення; 8) рівняння зміни зміщення; 9) рівняння зміни швидкості; 10) рівняння зміни прискорення.
Розв’язання. За графіком визначаємо: 1) Хм = 10 см; 2) Т = 0,2 с; 3)  ; 4)
; 4)  ; 5)
; 5) 
6) 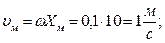 7)
7) 
8) Виходячи з рівняння коливань x(t) = Хм sіn(ωt + φ0), маємо
x(t) = 10 sіn(0,1πt +  ), cм.
), cм.
9) υ(t) = x'(t) = [10 sіn(0,1πt +  )]' = πcos(0,1πt +
)]' = πcos(0,1πt +  ) см/с.
) см/с.
10) а (t) = υ'(t) = [πcos(0,1πt +  )]' = – π2sіn(0,1πt +
)]' = – π2sіn(0,1πt +  ) см2/с.
) см2/с.
Завдання для самостійного розв’язування
1. Власна частота коливань залізного мосту 2 Гц, частота вібрації електродвигуна 2500 Гц. Визначити періоди цих коливань. Скільки коливань здійснюють ці об’єкти за 1 год?
2. В однакових чи протилежних фазах коливаються: 1) крила птаха, що летить; 2) руки людини під час веслування на човні; 3) склоочисники на автомобілях?
3. Швидкість коливальної точки змінюється за законом  , м/с. Визначити: 1) амплітуду швидкості; 2) циклічну частоту; 3) початкову фазу; 4) частоту; 5) період; 6) амплітуду зміщення; 7) амплітуду прискорення; 8) рівняння залежності зміщення від часу; 9) рівняння зміни прискорення.
, м/с. Визначити: 1) амплітуду швидкості; 2) циклічну частоту; 3) початкову фазу; 4) частоту; 5) період; 6) амплітуду зміщення; 7) амплітуду прискорення; 8) рівняння залежності зміщення від часу; 9) рівняння зміни прискорення.
4. 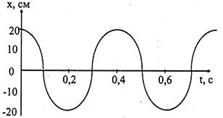 За графіком х (t) визначити 1) амплітуду зміщення; 2) циклічну частоту; 3) початкову фазу; 4) частоту; 5) період; 6) амплітуду швидкості; 7) амплітуду прискорення; 8) рівняння зміни швидкості; 9) рівняння зміни прискорення.
За графіком х (t) визначити 1) амплітуду зміщення; 2) циклічну частоту; 3) початкову фазу; 4) частоту; 5) період; 6) амплітуду швидкості; 7) амплітуду прискорення; 8) рівняння зміни швидкості; 9) рівняння зміни прискорення.
5. Чому при певній швидкості автобуса скло його вікон починає деренчати?
6. Як і чому зміниться амплітуда коливань тіла при перенесенні його з повітря у воду?
Тема 2. Маятники
Маятники є коливальними системами, які за певних умов здійснюють гармонічні механічні коливання.
Математичний маятник
Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці.
Це ідеальна коливальна система.
Підвісимо матеріальну точку масою m на нитці довжиною l і відхилимо отриманий маятник на кут α від положення рівноваги. На тіло діятимуть (якщо знехтувати силами тертя і опору повітря) сила тяжіння  і сила натягу нитки
і сила натягу нитки  , рівнодійна яких
, рівнодійна яких  і буде надавати матеріальній точці прискорення
і буде надавати матеріальній точці прискорення  , яке буде напрямлене в бік положення рівноваги. Модуль рівнодійної цих сил (повертальної сили) знаходимо із прямокутного трикутника FOA:
, яке буде напрямлене в бік положення рівноваги. Модуль рівнодійної цих сил (повертальної сили) знаходимо із прямокутного трикутника FOA:
F = mgsinα.
У разі малих кутів відхилення sinα ≈ α = x/l. Bраховуючи, що напрям зміщення і повертальної сили протилежні, отримаємо


де х – абсолютне значення зміщення маятника від положення рівноваги. Оскільки за ІІ законом Ньютона  , то прискорення маятника
, то прискорення маятника  , де
, де  . Звідки циклічна частота математичного маятника
. Звідки циклічна частота математичного маятника

Період коливань математичного маятника

Згідно з цією формулою можна зробити висновок, що період коливань математичного маятника не залежить від маси тіла, а визначається лише довжиною підвісу і прискоренням вільного падіння (закон Гюйгенса).
2.2. Фізичний маятник
Якщо подібний маятник не можна вважати матеріальною точкою або не можна знехтувати вагою тіла і розтягом підвісу, то маятник називають фізичним. Такий маятник коливається подібно до математичного.
 2.3. Пружинний маятник
2.3. Пружинний маятник
Ще одним прикладом гармонічного коливання є коливання тіла на пружині. У стані рівноваги (положення х = 0) пружина поки що не деформована, тому на тіло сила пружності не діє. Сила тертя між тілом і опорою дорівнює нулю. Сила тяжіння зрівноважена силою реакції опори. Якщо вивести тіло зі стану рівноваги, перемістивши його вздовж осі Ох на відстань x = ± A (ліворуч або праворуч), а потім відпустити, то маятник буде вільно коливатися під дією сили пружності за законом x = Asinωt. Згідно із законом Гука Fпр.х = – kx. За другим законом Ньютона Fпр.х = ma, де m – маса тіла пружинного маятника; а – його прискорення, або  , де
, де
 .
.
Циклічна частота коливань пружинного маятника.
Період коливань пружинного маятника
 .
.
Як видно з формул період і частота коливань пружинного маятника не залежать від прискорення вільного падіння, а визначаються лише масою підвішеного тіла і жорсткістю пружини.
2.4. Перетворення енергії при гармонічних коливаннях
Розглянемо перетворення енергії під час гармонічних коливань на прикладі пружинного маятника. Вважатимемо систему, що виконує вільні гармонічні коливання під дією пружної сили замкненою. У процесі коливання згідно із законом збереження енергії відбувається перетворення кінетичної енергії в потенціальну і, навпаки, але повна механічна енергія замкненої системи має залишатися незмінною.
З цією метою з’ясуємо, як змінюється в часі кінетична і потенціальна енергії. У формулу кінетичної енергії

підставимо значення швидкості гармонічного коливання  . Отримаємо
. Отримаємо

Якщо в певну мить зміщення системи від положення рівноваги дорівнює х, то її потенціальна енергія дорівнює роботі пружної сили. Оскільки під час зміни зміщення від 0 до х величина пружної сили змінюється від F1 = 0 до F2 = kx, то роботу цієї сили розраховують за формулою  . Отже,
. Отже,

Підставляючи в цю формулу значення зміщення для гармонічного коливання  , одержимо вираз
, одержимо вираз
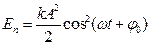
Повна енергія коливальної системи дорівнює сумі кінетичної і потенціальної енергій у заданий момент часу. Тоді, враховуючи, що mω2 = k,  , отримаємо:
, отримаємо:

Таким чином, повна енергія системи, що виконує гармонічні коливання, пропорційна квадрату амплітуди коливань і не залежить від часу

Зі збільшенням кінетичної енергії системи зменшується її потенціальна енергія і, навпаки, але сума кінетичної і потенціальної енергій в довільний момент часу залишається сталою.
Приклади розв’язування задач
1. Як зміниться період коливань математичного маятника, якщо довжину нитки збільшити в 2 рази?
 Дано: Розв’язання:
Дано: Розв’язання:



 –? Період коливань маятника збільшиться у 2 рази.
–? Період коливань маятника збільшиться у 2 рази.
2. Вантаж, прикріплений до пружини, здійснює гармонічні коливання в горизонтальній площині. Як зміниться частота коливань вантажу, якщо масу вантажу збільшити в 9 разів?
 Дано: Розв’язання:
Дано: Розв’язання:
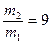


 –? Частота коливань вантажу зменшиться у 3 рази.
–? Частота коливань вантажу зменшиться у 3 рази.

3. Вантаж масою 25 кг висить на шнурі довжиною 2,5 м. На яку найбільшу висоту можна відхилити в сторону вантаж, щоб при наступних вільних коливаннях шнур не обірвався? Шнур може витримати натяг в 550 Н.
 Дано: Розв’язання:
Дано: Розв’язання:
m= 25кг Дану систему можна вважати ізольованою.
l= 2,5 м Нульовий рівень потенціальної енергії сумісний з
Fн= 550 Н найнижчим положенням тіла (рис.).
h –? Запишемо закон збереження енергії:
Ек1 + Еп1 = Ек2 + Еп2
У положенні 1: Ек1 = 0; Еп1 = mgh. У положенні 2:  ; Еп2 = 0.
; Еп2 = 0.
Отже, 
 .
.
Швидкість можна знайти з II закону Ньютона:
 . В проекції на вертикальну вісь:
. В проекції на вертикальну вісь:  ,
,
де  – доцентрове прискорення, l – довжина шнура, вона дорівнює радіусу дуги, по якій рухається вантаж. Звідси:
– доцентрове прискорення, l – довжина шнура, вона дорівнює радіусу дуги, по якій рухається вантаж. Звідси:
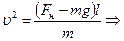
 .
.

 .
.
Завдання для самостійного розв’язування
1. Як зміниться періоди коливань математичного і пружинного маятників, якщо амплітуду коливань зменшити в 2 рази? Тертя відсутнє.
2. При гармонічних коливаннях математичного маятника вантаж проходить шлях від правого крайнього положення до положення рівноваги за 0,5 c. Який період і частота коливань маятника?
3. Визначити масу кульки, що коливається на пружині у горизонтальній площині з періодом 20 с. Коефіцієнт жорсткості пружини 1 кН/м.
4. Яка довжина математичного маятника, що коливається з циклічною частотою 2π рад/с?
5. Вантаж, прикріплений до пружини, здійснює гармонічні коливання в горизонтальній площині. Як зміниться період коливань, якщо масу вантажу і жорсткість пружини збільшити в 2 рази?
6. При гармонічних коливаннях пружинного маятника з періодом 1 с і амплітудою 12 см тіло досягло мінімальної швидкості. Чому рівна у цей момент координата тіла?
7. Чи зміниться період коливань гойдалки, якщо: 1) на неї сядуть спочатку одна, а потім дві людини; 2) гойдаються спочатку сидячи, а потім стоячи?
8. Середня швидкість руху поршня парової машини 5,0 м/с, хід поршня 250 мм. Визначити частоту і період коливань поршня.
9. Підвішена до пружини гиря коливається по вертикалі з амплітудою 4 см. Визначити повну енергію коливань гирі, якщо коефіцієнт жорсткості пружини 1 кН/м.
10. Маятник завдовжки 100 см, маса якого 10 г, відхилили від положення рівноваги на кут 600 і відпустили. Визначити потенціальну енергію маятника на початку руху і кінетичну в прямовисному положенні.
11. Яку енергію має математичний маятник масою 100 г та довжиною нитки 1 м, якщо амплітуда коливань становить 40 см?
12. Вантаж на пружині із жорсткістю 1 кН/м здійснює коливання з амплітудою 2 см. Знайти кінетичну та потенціальну енергії, якщо фаза коливань π/3 рад.
13. На нитці завдовжки l підвісили кульку. Якої найменшої горизонтальної швидкості треба надати кульці, щоб вона відхилилася до висоти точки підвішування?
Тема 3. Хвилі
3.1. Основні поняття
Хвиля – процес поширення коливань у просторі з часом. Як і коливання, хвилі за своєю фізичною природою поділяють на механічні та електромагнітні.
Механічна хвиля – це процес поширення механічних коливань у пружному середовищі.
Прикладом найпоширеніших механічних хвиль є звук, хвилі на поверхні рідин.
Джерело хвилі – це коливальна система, яка під час коливань передає частину своєї енергії в навколишнє середовище. Ця передача має місце, коли частинки навколишнього пружного середовища беруть участь у коливальному процесі джерела.
Хвильова поверхня – неперервне геометричне місце точок, які коливаються в однакових фазах.
Фронт хвилі – передня хвиля, найбільш віддалена від джерела.
Промінь – лінія, вздовж якої поширюється фронт хвилі. В ізотропному середовищі промінь перпендикулярний до фронту хвилі.
3.2. Особливості хвильового процесу
Хвильовий процес не супроводжується перенесенням речовини в напрямі поширення хвилі. У кожній точці простору частинки лише здійснюють коливання відносно положення рівноваги. Але поширення коливань супроводжується передачею енергії коливань від однієї точки середовища до іншої.
Види хвиль
| Поздовжні | Поперечні |
| частинки середовища коливаються в тій самій площині, в якій поширюється і сама хвиля | частинки пружного середовища коливаються в площині, перпендикулярній до напряму поширення хвилі |

| 
|
| поширюється в твердих тілах, рідинах і газах | поширюватися в твердих тілах або на поверхні рідин |
Параметри хвиль
Графік коливань показує, як змінюється координата однією точки, що коливається, з часом. У хвилі коливаються всі точки, що її утворюють. Тому графік хвилі показує, як залежить координата всіх точок хвилі від їх положення у хвилі.


1. ПеріодомТ (с) хвилі є період коливань точок середовища (тобто джерела) під дією цієї хвилі.
2. Частотою хвилі ν (Гц) називають величину, обернену періоду, яка дорівнює кількості коливань точок, здійснених за 1 с.
3. Довжина хвилі λ (м) – найкоротша відстань між точками хвилі, які коливаються в однакових фазах і дорівнює відстані, яку пробігає хвильова поверхня за один період. (див. рис.)
4. Фазова швидкість υ (м/с) – швидкість поширення коливань у пружному середовищі
Зв’язок параметрів хвиль
 або
або 
Під час виникнення хвиль їх частота визначається частотою коливань джерела хвиль, а швидкість залежить від властивостей середовища. Тому хвилі однієї і тієї ж частоти мають різну довжину в різних середовищах.
 3.5. Рівняння хвилі
3.5. Рівняння хвилі
Знайдемо формулу, що описує процес поширення коливань в середовищі. Нехай джерело хвиль (т. О на рис.) коливається за гармонічним законом x = Asinωt, де х – зміщення точки середовища, А – амплітуда коливань, ω = 2πν – циклічна частота, t – час від початку коливань джерела хвиль. Точка М середовища знаходиться на відстані у від джерела хвиль. Швидкість поширення хвилі – величина скінченна, тому чим далі знаходиться ця точка середовища від джерела, тим більше часу потрібно для того, щоб хвиля надійшла до цієї точки, і тим пізніше в ній почнуться коливання. Отже,  – це час запізнення початку коливань в заданій точці середовища порівняно з джерелом хвиль. Тому час коливання даної точки середовища
– це час запізнення початку коливань в заданій точці середовища порівняно з джерелом хвиль. Тому час коливання даної точки середовища

Тому підставивши рівняння (8) у вираз (7), дістанемо

Формула (9) є рівнянням плоскої біжучої хвилі.
 3.6. Хвильові властивості
3.6. Хвильові властивості
Принцип Гюйгенса
 Кожна точка поверхні, якої досягла в даний момент хвиля, є точковим джерелом вторинних хвиль, причому поверхня, дотична до цих вторинних хвиль, буде хвильовою поверхнею в наступний момент часу
Кожна точка поверхні, якої досягла в даний момент хвиля, є точковим джерелом вторинних хвиль, причому поверхня, дотична до цих вторинних хвиль, буде хвильовою поверхнею в наступний момент часу
При падінні на плоску межу поділу двох різних середовищ плоска хвиля частково відбивається, частково проходить в інше середовище, залишаючись плоскою, але міняє при цьому свій напрям поширення (заломлюється).
2. Поглинання – зменшення енергії, яку переносить хвиля внаслідок зменшення внутрішнього тертя середовища.
3. Відбивання – частина енергії падаючої хвилі відбивається назад у перше середовище на межі поділу середовищ.
4. Заломлення – зміна напряму поширення хвилі при переході з одного середовища в інше.
5. Інтерференція – явище додавання (накладання) двох когерентних хвиль у просторі, внаслідок чого спостерігається стійка в часі інтерференційна картина – постійний у часі розподіл амплітуд результуючої хвилі у різних точках простору,при якому відбувається стійке в часі їх взаємне підсилення в одних точках простору і ослаблення в інших, залежно від співвідношення між фазами цих хвиль.
 Когерентні хвилі збуджуються джерелом, які коливаються з однаковою частотою і постійною у часі різницею фаз.
Когерентні хвилі збуджуються джерелом, які коливаються з однаковою частотою і постійною у часі різницею фаз.
| Максимум інтерференційної картини | Мінімум інтерференційної картини |


| 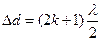

|
k = 1, 2, 3,…, n (ціле число); λ – довжина хвилі, Δd – різниця ходу хвиль.



Картина інтерференції двох кругових когерентних хвиль у залежності від довжини хвилі та відстані між джерелами
 Стояча хвиля – виникає внаслідок інтерференції прямої і відбитої від перешкоди біжучих хвиль.
Стояча хвиля – виникає внаслідок інтерференції прямої і відбитої від перешкоди біжучих хвиль.
Стояча хвилястійка, якщо на довжині L укладається ціле число півхвиль.
Стояча хвиляне переносить енергію в просторі. Вузли А і пучності N в просторі не переміщаються.
6. Дифракція – явище порушення закону прямолінійного поширення хвиль в однорідному середовищі або огинання хвилями перешкод.
Умова спостереження дифракції – довжина хвилі сумірна з розмірами щілини або перешкоди: λ ~ d (за щілиною поширюється сферична хвиля так, ніби в отворі екрана міститься джерело хвиль (рис. а). Якщо d >>λ (рис. б), форма хвильового фронту після проходження через щілину майже не змінюється. На рис. в – дифракція хвиль на воді




а б в г
Принцип Гюйгенса-Френеля
Дифракція зумовлена інтерференцією вторинних хвиль (рис. г).
Приклади розв’язування задач
1. За 30 с морська хвиля вдаряється об берег 15 разів. Швидкість поширення хвилі дорівнює 4 м/с. Яка довжина морської хвилі?
 Дано: Розв’язання:
Дано: Розв’язання:
|
υ = 4 м/с
N = 15
λ –?
2. Човен гойдається на хвилях, яка поширюється із швидкістю 1,5 м/с. Визначити період коливань човна, якщо відстань між найближчими гребнями хвиль становить 6 м.
 Дано: Розв’язання:
Дано: Розв’язання:
υ = 1,5 м/с 


λ = 4 см
Т –?
3. Різниця ходу двох когерентних хвиль із рівними амплітудами коливань дорівнює 8 см, а довжина хвиль – 4 см. Який результат інтерференції?
 Дано: Розв’язання:
Дано: Розв’язання:
Δl = 8 cм 

 ;
; 
λ = 4 см спостерігається максимум інтерференційної картини
k –?
Завдання для самостійного розв’язування
1. Визначити різницю фаз коливань двох точок, віддалених від джерела коливань на 3,5 та 2,0 м, якщо період коливань 0,5 с, а коливання поширюються з швидкістю 6 м/с.
2. Човен гойдається на хвилях, які поширюються з швидкістю 2,5 м/с. Відстань між двома найближчими гpeбнями хвиль 8 м. Визначити період коливання човна.
3. Людина, стоячи на березі моря, визначила, що відстань між двома гребнями хвиль, які йдуть один за одним, становить 8 м. Крім тoгo, людина підрахувала, що за 60 с повз неї пройшло 23 гpeбні хвиль. Визначити швидкість поширення хвилі.
4. Відстань між першим та четвертим вузлами стоячої хвилі 24 см. Визначити довжину біжучої хвилі.
5. Шнур завдовжки 3 м, один кінець якого прив’язаний, розгойдали з частотою 5 Гц, утворивши стоячі хвилі. На ньому вмістилося 6 півхвиль. Визначити швидкість поширення хвиль у шнурі.
Тема 4. Звукові хвилі
4.1. Звуком або звуковими хвилями називають механічні хвилі, які створюються тілом, частота коливань якого лежить в межах від 16 до 20 000 Гц. Ця хвиля сприймається органами слуху людини. Такі коливання називають ще акустичними. Розділ фізики, який вивчає способи збудження звукових хвиль, їх поширення і взаємодію з середовищем, називають акустикою.
 Розділ фізики, в якому вивчаються звукові явища, називають акустикою.
Розділ фізики, в якому вивчаються звукові явища, називають акустикою.
Джерелом звуку є тіло, що коливається. Це підтверджено експериментально. Якщо, наприклад, завдати удару по камертону і піднести до нього малу кульку, то звук можна буде чути доти, доки кулька буде відскакувати від камертона, що свідчить про його коливання. У більшості випадків джерела звуку – це тверді тіла (струни, мембрани, деки, дифузори, п’єзопластинки тощо). Існують й інші джерела: повітряні стовпи у духових інструментах, завихрення повітря під час турбулентного обтікання куль, мін, снарядів, надзвукових літаків, досить рідко – коливання рідин.
У твердих тілах звук поширюється у вигляді поздовжніх і поперечних хвиль. У рідинах і газах, оскільки в них деформація зсуву неможлива, звукові хвилі поширюються тільки у вигляді поздовжніх хвиль.
Характеристики звуку
| акустичні (фізичні) | фізіологічні |
| швидкість поширення | |
| Інтенсивність | гучність |
| Частота | висота |
| Амплітуда | тембр |
1. Швидкість звуку

де s – відстань від джерела до приймача звуку, t – час поширення звуку від джерела до приймача звуку, Т – період, ν – частота, λ –
довжина звукової хвилі.
Швидкість поширення звуку залежить від роду середовища, його стану, що виражається густиною ρ, та пружних властивостей, що виражається модулем Юнга Е:
 .
.
Швидкість поширення звуку залежить від температури. Наприклад, швидкість звуку у рідинах (крім води) з підвищенням температури зменшується, а в газах, навпаки – при підвищенні температури за постійного тиску – збільшується.
Швидкості звуку в різних середовищах
| Речовина | Швидкість звуку, м/с |
| Вуглекислий газ (0°С) | |
| Повітря (при 20 °C) | |
| Водень | 1 284 |
| Вода | 1 483 |
| Морська вода | 1 530 |
| Гума | 1 800 |
| Дерево | 3 320 |
| Залізо | 5 850 |
Залежність швидкості звуку в повітрі від температури
| t, 0С | υ, м/с |
Висота звуку
Звуки, які ми чуємо щодня, дуже різноманітні. Прийнято розрізняти такі звуки: 1) музичні, або тони; 2) шуми і 3) удари. До музикальних звуків належать спів, звучання натягнутих струн музичних інструментів тощо. До шумів належать звуки від вібрації верстатів, вибухів, роботи двигунів, оплески, шерех, скрипіння, приголосні звуки мови тощо. Удари – це різкі короткочасні звуки.
Сприймаючи музикальні звуки, людина розрізняє їх за висотою.
Висота звуку звукової хвилі – фізіологічний параметр звуку, що визначається частотою. Більшій частоті відповідає вищий звук.
Діапазон звукових коливань, що відповідає подвійній зміні частоти коливань, називають октавою.
Звукові хвилі, як правило, мають складну форму, але багато звуків можна подати як суму синусоїдальних, тобто гармонічних коливань, їх називають музичними. Окрема синусоїдальна звукова хвиля називається чистим тоном. Джерелом такої хвилі є камертон. У загальному випадку музичні звуки складні, тобто мають певний набір коливань різних частот. Найменша частота складного звуку називається першою гармонікою або основним тоном звукової хвилі. Тони, що супроводжують основний тон, називають обертонами. Музикальні звуки з одним і тим самим основним тоном відрізняються тембром, який визначається наявністю обертонів – їх частотами й амплітудами. Завдяки цьому ми чітко відрізняємо звучання однієї ноти різних голосів чи інструментів.
На відміну від музичних звуків, шуми є складною сумішшю величезної кількості коливань з різними частотами.
3. Інтенсивність (сила) звуку
Це фізична характеристика, яка характеризує перенесення енергії Е звуковою хвилею за одиницю часу t через одиницю площі S, яка перпендикулярна до напряму поширення звуку
 .
.
де 
– інтенсивність джерела звуку.

Інтенсивності відповідає психофізіологічна характеристика – гучність, яка вимірюється у децибелах, названа на честь американського вченого Белла – винахідника телефону і слухового апарату для глухих.
Гучність звуку визначається середнім тиском звуку на органи слуху людини, тому є поняттям суб’єктивним. Один і той самий звук сприймається одними людьми тихим, іншим – гучним, голосним.
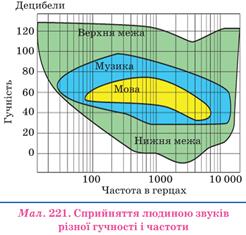 Чутливість органів слуху людини має нижній і верхній поріг чутності і залежить від частоти звуку. У межах частот 700-6000 Гц нижня межа чутності дорівнює 2·10-12Вт/м2, що відповідає 0 дБ. Верхній поріг чутності, який викликає больові відчуття досягає ≈ 10 Вт/м2, що відповідає 130 дБ і при тривалій дії може призвести до безповоротної втрати слуху.
Чутливість органів слуху людини має нижній і верхній поріг чутності і залежить від частоти звуку. У межах частот 700-6000 Гц нижня межа чутності дорівнює 2·10-12Вт/м2, що відповідає 0 дБ. Верхній поріг чутності, який викликає больові відчуття досягає ≈ 10 Вт/м2, що відповідає 130 дБ і при тривалій дії може призвести до безповоротної втрати слуху.
Крім того гучність пов’язана з амплітудою коливань – чим більша амплітуда, тим гучніший звук.
Рівні різних звуків
| Рівень гучності, дБ | Інтенсивність звуку, Вт/м2 | Звуковий тиск, Н/м2 | Наближений характер звуку |
| 10-12 | 2,0 · 10-5 | Межа чутності Повна тиша | |
| 10-11 | 6,3 · 10-5 | Серцеві тони через стетоскоп Шепіт на відстані 1 м Тихий шелест листя Цокання ручного механічного годинника | |
| 10-10 | 2,0 · 10-4 | Звуковий комфорт Тиха розмова (майже пошепки) Звуки в тихому лісі | |
| 10-9 | 6,3 · 10-4 | Норма гучності звуку вночі Звуки в тихій кімнаті | |
| 10-8 | 2,0 · 10-3 | Гігієнічна норма гучності звуку вдень Розмова звичайна Негучна музика | |
| 10-7 | 6,3 · 10-3 | Шум у закладі | |
| 10-6 | 2,0 · 10-2 | Звичайна розмова на відстані 1 м Шум на пожвавленій вулиці Шосе з помірним рухом | |
| 10-5 | 6,3 · 10-2 | Гучна розмова Двигун вантажного автомобіля | |
| 10-4 | 0,2 | Шум станка Шум на шосе з інтенсивним рухом | |
| 10-3 | 0,63 | Шумовий поріг початку руйнування слуху в людини Максимальна норма гучності звуку в промислових приміщеннях Автомобільний гудок Шум у потязі метро (при 100 км/год) | |
| 10-2 | Голос співака Автосирена Шум у метро при проходженні потяга | ||
| 10-1 | 6,3 | Шум авіамотора Запуск ракети Пневматичний молоток Швидкий поїзд (300 км/год) | |
| Больові відчуття Потужний гуркіт грому Рок-концерт Реактивний двигун літака на зльоті | |||
| Руйнівний для слуху поріг(больова межа). Надшумна електромузика |
Шкала звукових хвиль
| Частота, Гц | Найменування | Засоби збудження | Застосування |
| 0 – 20 | Інфразвуки | Коливання води у великих водоймах, биття серця | Передбачення погоди, діагностика захворювань серця |
| 16 – 2·104 | Чутні звуки | Голос людини та тварин, музикальні інструменти, свистки, сирени, гучномовці, тощо | Для зв’язку та сигналізації, а також вимірювання відстаней (звукометрія) |
| 2·104 – 1010 | Ультразвуки | Магнітострикційні та п’єзоелектричні випромінювачі, свисток, також деякими тваринами та комахами (летючі миші, цвіркуни, сарана тощо) | Гідролокація, очищення деталей, дефектоскопія деталей та будівельних конструкцій, прискорення хімічних реакцій, медичні та біологічні дослідження, молекулярна фізика |
| 1011 і більше | Гіперзвуки | Теплові коливання молекул | У наукових дослідженнях |
4.4.Властивості звукових хвиль
Звукова хвиля, як і будь-яка інша, на межі поділу двох середовищ (наприклад, при зустрічі зі стіною, деревом тощо) частково поглинається нею, частково гаситься і частково відбивається. При цьому спостерігаються цікаві акустичні явища.
Поглинання
Є матеріали, наприклад пористі панелі, пінопласт, в яких звукові коливання швидко затухають. Це використовується, наприклад, для звукоізоляції приміщень. Чим більше предметів у приміщенні, тим більше коефіцієнт поглинання звуку. Наприклад, оштукатурювання стін поглинає близько 8 % енергії звукових хвиль, килими – до 20 %.
2. Відбивання
Луна – повернення звукової хвилі до свого джерела після відбивання від поверхні, яка розміщена перпендикулярно до променя цієї хвилі. Особливо ефектне це явище на великих відкритих ділянках лісів, в ущелинах гір (тобто при великій відстані між джерелом і перешкодою досить велика).



 Реверберація – залишкове звучання в закритому приміщенні, яке є наслідком багаторазового відбивання звуку від стін приміщення. Чим менше предметів у приміщенні, тим довше триває реверберація. Час реверберації дуже впливає на якість звуку у концертних, музейних залах, тому при їх конструюванні цей ефект обов’язково враховується.
Реверберація – залишкове звучання в закритому приміщенні, яке є наслідком багаторазового відбивання звуку від стін приміщення. Чим менше предметів у приміщенні, тим довше триває реверберація. Час реверберації дуже впливає на якість звуку у концертних, музейних залах, тому при їх конструюванні цей ефект обов’язково враховується.
Відбивання звукових (а частіше – ультразвукових) хвиль використовується для визначення глибини моря, виявлення дефектів у різних виробах, медичній діагностиці.
Гуркіт і розкати грому – багаторазове відбивання від хмар і поверхні Землі і часткове поглинання ними звукових хвиль.
3. Інтерференція звуку


4. Дифракція звуку на отворі

| 
|
| λ >> d | λ >> d |
| фронт хвилі за отвором – півсфера | хвиля майже не розходиться в сторони. |
5. Ефект Доплера – залежність сприймання параметрів хвилі в разі наближення (рис. а) і віддалення (рис. б) джерела від спостерігача.


Частота сприйнятого звуку при наближенні джерела до приймача  .
.
Частота сприйнятого звуку при віддаленні джерела
 .
.
Акустичний (звуковий) резонанс
Якщо частота власних коливань тіла збігається з частотою звукової хвилі, то умови для передавання енергії від звукової хвилі до тіла виявляються найкращими – тіло стає акустичним резонатором. Амплітуда вимушених коливань при цьому досягає максимального значення – спостерігається акустичний резонанс. До резонаторів можна віднести деякі деки і труби в музичних інструментах, тощо. Голова людини (точніше порожнина рота) теж є резонатором, завдяки чому звук голосу значно підсилюється. Це пояснює те, що ми часто не впізнаємо свій голос при запису чи при підсилюванні його за допомогою мікрофона, хоча для інших він звучить звично.
Акустичний резонанс спостерігається при виникненні звукової хвиліу камертонавнаслідок збудження іншого камертона при розміщенні їх ящиків отворами навпроти.
Фігури Хладні – фігури, що утворюються скупченням дрібних частинок сухого піску, цукру тощо поблизу вузлових ліній на поверхні пружної пластинки, яка коливається, коли по її краю проводити смичком (або подібної механічної системи). Кожному власному коливанню пластинки відповідає своє розташування вузлових ліній. Фігури Хладні названі по імені німецького фізика Ернеста Флореса Фрідріха Хладні, що виявив їх. В разі круглої пластинки вузлові лінії можуть бути кругами або радіальними; в разі прямокутної або трикутної пластинки вони мають напрям, паралельний сторонам або діагоналям. Міняючи точки закріплення і місця збудження, можна отримати всілякі Хладні-фігури, відповідні різним власним коливанням пластинки. Хладні-фігури застосовуються для вивчення власних частот діафрагм телефонів, мікрофонів, гучномовців тощо.


Ультразвуки
Ультразвуки у природі трапляються рідко. Кажани використовують ультразвук для орієнтування у темряві. Складний і потужний ультразвуковий локатор мають дельфіни.
 Ультразвукова хвиля порівняно із звуковою має більшу інтенсивність за рахунок більшої частоти коливань в ній. Це використовують в різних галузях. Завдяки спрямованості ультразвукових хвиль і їх відбиванню від перешкод можна знайти відстань до предмета:
Ультразвукова хвиля порівняно із звуковою має більшу інтенсивність за рахунок більшої частоти коливань в ній. Це використовують в різних галузях. Завдяки спрямованості ультразвукових хвиль і їх відбиванню від перешкод можна знайти відстань до предмета:

Звуколокатори (їх називають також ехолокаторами) дають змогу виявити і визначити місцезнаходження різних пошкоджень у виробах (порожнечі, тріщини, сторонні включення). У медицині ультразвук використовують для діагностики і лікування деяких захворювань.
Ультразвукові хвилі великої інтенсивності використовують для виготовлення порошків та емульсій з речовин, які не змішуються, тощо.
Інфразвуки
У природних умовах інфразвуки можуть зумовити помахування крил птахів, коливання гілок дерев чи поверхні моря під впливом вітру. Існують інфразвуки техногенного походження. Ці низькочастотні хвилі слабко поглинаються і тому здатні поширюватися на великі відстані. Птахи і більшість тварин чутливі до цих звукових хвиль. Припускають, що завдяки цьому від інфразвуків, що передують землетрусам, тварини стривожуються, а люди й гадки не мають про небезпеку.
Інфразвуки ще не знайшли широкого застосування. Однак їх властивості необхідно вивчати, щоб запобігти негативному впливу на здоров’я людини. Під час тривалих дій потужних інфразвуків у людини з’являються симптоми, подібні до симптомів «морської хвороби». Водночас існують новітні методи лікування хвороб дозованими імпульсами інфразвуків.
4.6. Екологічні проблеми акустики
Звуки великої гучності, зокрема шуми, наносять шкоду навколишньому середовищу. Передозування інтенсивності інфра- і ультразвукових хвиль під час лікування деяких хвороб також є небезпечним. «Забруднення» навколишнього середовища акустичними коливаннями шкідливо впливає на здоров’я людини. З метою охорони навколишнього середовища забороняється подавати з автомобілів звукові сигнали в населених пунктах, будувати летовища у






 ;
;