Случайным событием или просто событием называется любая совокупность исходов опыта.
Исход опыта, при котором наступает данное событие, называется благоприятствующим или благоприятным.
Событие считается наступившим, если имеет место один из благоприятствующих исходов.
Объединением (суммой) двух событий А, В называется событие, состоящее в наступлении хотя бы одного из них.
Объединение событий обозначается А + В или A È В (читается: А или В). Событие А + В представляет собой совокупность исходов, каждый из которых принадлежит хотя бы одному из событий А, В.
Произведением (пересечением) двух событий А, В называется событие, состоящее в наступлении их обоих.
Произведение событий обозначается А • В, или АВ, или
А Ç В (читается: А и В). Событие А • В представляет собой совокупность исходов, принадлежащих каждому из событий А, В.
Равновозможными называются исходы, возможности наступления которых в силу объективных причин должны быть одинаковы.
Вероятность случайного события А – это отношение числа исходов М А, благоприятствующих событию А, к общему числу равновозможных несовместных исходов N:
РА = M A/ N. (1.3.1)
Достоверным называется событие, которое в результате эксперимента должно произойти обязательно. Такое событие представляет собой множество всех элементарных исходов, и обозначается буквой W. Вероятность достоверного события принимают за единицу: Р(W) = 1.
Невозможным называется событие, которое в данном опыте произойти не может. Невозможное событие обозначают символом Æ. Вероятность невозможного события принимают за ноль: Р(Æ) = 0.
К этим свойствам вероятности добавляют еще две аксиомы:
1. Вероятность любого события А лежит между нулем и единицей: 0 £ РА £ 1.
2. Для несовместных событий:
Р(А + В) = Р(А) + Р(В). (1.3.2)
Эту аксиому иногда называют 1-й теоремой сложения вероятностей: вероятность объединения несовместных событий равна сумме вероятностей этих событий.
События А и В называются независимыми, если факт наступления одного из них не меняет вероятности наступления другого.
Для независимых событий теорема умножения вероятностей имеет следующий вид: вероятность события, которое является произведением независимых событий А и В, равна произведению их вероятностей:
Р(А • В) = Р(А) •Р(В). (1.3.3)
Следующий результат обобщает аксиому сложения вероятностей для объединения двух произвольных событий:
Р(А + В) = Р(А) + Р(В) – Р(А • В). (1.3.4)
Рассмотрим примеры решения задач.
Пример 1. Игроки А и В играют, бросая по 2 кости. Игрок А выигрывает в том случае, когда сумма выпавших очков равна 7. Игрок В выигрывает в том случае, когда сумма выпавших очков равна 8. Кому выгодна эта игра?
Решение. Выпадения различных граней одной игральной кости (однородного куба) – это события очевидно равновозможные и несовместные, так как две грани одновременно выпасть не могут. Построим множество W для задачи одновременного бросания двух костей. Мы имеем W1 = (1, 2, 3, 4, 5, 6) и W2 = (1, 2, 3, 4, 5, 6). Множество W формируется из всех возможных комбинаций выпавших граней и состоит из 36 элементов, записанных в таблице.
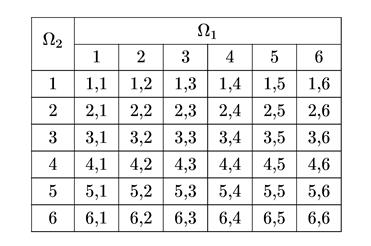
Игроку А (событие А) благоприятствуют 6 исходов (1,6; 6,1; 2,5; 5,2; 3,4; 4,3), а игроку В (событие В) – только 5 исходов (1,6; 6,2; 5,3; 3,5; 4,4). Общее число исходов – 36. Используя формулу (1.3.1), найдем: P(А) = 6/36, Р(В) = 5/36. Таким образом, игроку А игра выгоднее.
Пример 2. Пусть в одной урне находятся 5 черных и 10 белых шаров, а в другой урне – 3 черных и 17 белых. Найти вероятность того, что при извлечении по одному шару из каждой урны оба шара окажутся черными.
Решение. Событие А – извлечение черного шара из первой урны, событие В – извлечение черного шара из второй урны. По формуле (1.3.1) имеем: Р(А) = 5/15 = 1/3; Р(В) = 3/20.
Событие А • В – оба шара имеют черный цвет. Из (1.3.3) следует: Р(А • В) = Р(А) • Р(В) = (1/3) • (3/20) = 1/20.
Ответ: 1/20.
Пример 3. Пусть в одной урне находятся 5 черных и 10 белых шаров, а в другой урне – 3 черных и 17 белых. Найти вероятность того, что при извлечении по одному шару из каждой урны хотя бы один шар окажется черным.
Решение. Используя значения Р(А), Р(В) и Р(А • В), полученные в предыдущем примере и исходя из формулы (1.3.4), найдем: Р(А + В) = 1/3 + 3/20 – 1/20 = 22/60.
Ответ: 22/60.
Случайные величины
Пусть дискретная случайная величина X задана таблицей
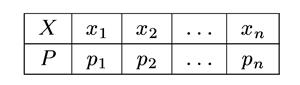
где р 1 + р 2 + … + р n = 1. (1.3.5)
Математическое ожидание дискретной случайной величины X:
М(X) =  . (1.3.6)
. (1.3.6)
(математическое ожидание имеет ту же размерность, что и случайная величина).
Дисперсия дискретной случайной величины X:
D(X) =  (1.3.7)
(1.3.7)
(дисперсия имеет размерность квадрата случайной величины).
Непрерывная случайная величина X может быть задана своей функцией распределения вероятностей или плотностью распределения вероятностей.
Плотность распределения вероятностей случайной величины X:
f X(x) = f (x) = d P/ dx.
Функция распределения вероятностей случайной величины X:
F X(x) = F (x) = P (X £ х),
P(x 1 < X < x 2) = F (x 2) – F (x 1). (1.3.5)
Связь функции распределения и плотности вероятностей:
f (x) = F (x)' = dF (x)/ dx,
F (x) =  .
.
Условие нормировки для непрерывной случайной величины:
 = l.
= l.
Математическое ожидание непрерывной случайной величины X:
М(Х) =  .
.
Дисперсия непрерывной случайной величины X:
D(X) =  .
.
Общие соотношения:
D(X) = М{[ Х – М(Х)]2}
или
D(X) = М(Х 2) – [М(Х)]2.
Среднее квадратическое отклонение случайной величины:
s (Х) = ÖР(X).
Плотность распределения вероятностей для нормального закона распределения (закона Гаусса):
f (x) = 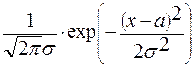 ,
,
где а – математическое ожидание случайной величины, s – среднее квадратическое отклонение.
Функция распределения вероятностей для нормального закона:
F (x) = Ф(t), (1.3.6)
где t = (х – а)/ s, значения функции Ф(t) даны в соответствующих таблицах.
Плотность распределения вероятностей для равномерного распределения на интервале [ а, b ]:
f (x) = 0 вне отрезка [ а, b ],
f (x) = 1/(b – а) при а £ х £ b.
Плотность вероятности для экспоненциального закона распределения:
f (x) = lехр (– lx), х ³ 0.
Распределение Больцмана:
n = n 0 exp (– mgh / kT),
где n – концентрация молекул, h – высота над уровнем Земли, m – масса молекулы, k – постоянная Больцмана, g – ускорение свободного падения.
Пример 4. Случайная величина распределена по нормальному закону с нулевым математическим ожиданием (а = 0) и средним квадратическим отклонением а. Найти вероятность того, что эта случайная величина принимает значения в интервалах:
а) – s < X < + s; б) – 2 s < X < + 2 s; в) – 3 s < X < +3 s.
Пример решения для интервала шириной s.
Согласно (1.3.5) и (1.3.6) запишем:
Р(– s < X < + s) = F (s) – F (– s) = Ф[(s – а)/ s ] – Ф[(– s – а)/ s ],
Ф[(s – 0)/ s ] = Ф(1) = 0,8413 (из таблицы),
Ф[(– s – 0)/ s ] = Ф(– 1) = 1 – Ф(1) = 1 – 0,8413 = 0,1587,
Р = Ф (1) – Ф (–1) = 0,8413 – 0,1587 = 0,6826.
Иллюстрация правила трех сигм.
Среди 10 000 значений нормальной случайной величины в среднем только 27 выйдут за пределы интервала (а – 3 s, а + 3 s). Это означает, что среди небольшого числа значений X практически нет таких, которые выходят за пределы указанного интервала.
Пример 5. Случайная величина X распределена по нормальному закону с математическим ожиданием 3 и дисперсией 4. Найти вероятность того, что 1 < X < 7.
Решение. а = 3, s = Ö4 = 2 найдем искомую вероятность (без вывода):
Р(1< X < 7) = [Ф{(7 – 3)/2} – Ф{(1 – 3)/2}] = [Ф(2) – Ф(–1)] =
= (0,9772 – 0,1587) = 0,8185.






