Если частица массы m движется со скоростью v, то ее кинетическая энергия может быть представлена в виде
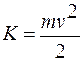. (1.3.57)
Кинетическая энергия системы частиц – величина аддитивная и представляет собой сумму кинетических энергий всех частиц системы:
,
где N – число частиц в системе, mi – масса i -той частицы, vi – скорость i -той частицы.
* Сила, работа которой не зависит от формы и длины пути (от траектории точки приложения силы), называется консервативной силой. Математически условие консервативности силы выражается в виде:
,
что означает:
* циркуляция консервативной силы по любому замкнутому контуру равна нулю.
Из определения консервативной силы следует:
работу консервативной силы можно представить как убыль некоторой скалярной функции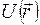 
, зависящей только от положения тела (частицы), которая называется потенциальной энергией:
Последняя формула является определением потенциальной энергии:
* Потенциальная энергия определена с точностью до произвольной постоянной.
Так как определена только разность потенциальной энергии, то к выражению для потенциальной энергии можно добавить или вычесть любую постоянную величину. Поэтому в каждом конкретном случае договариваются о начале отсчета потенциальной энергии (в какой именно точке считают U = 0).
Полная механическая энергия частицы – это сумма ее кинетической и потенциальной энергий:
Если на частицу действуют только консервативные силы, то с одной стороны dA = – dU, с другой (из второго закона Ньютона): dA = dK Þ – dU = dK,
d (K + U) = dE=0 Þ
Е = const (1.3.58)
Выражение (1.3.58) – это закон сохранения полной механической энергии, который гласит:
* механическая энергия частицы, подверженной действию только консервативных сил, сохраняется.
Неконсервативные силы – силы, работа которых зависит от длины и формы пути. То есть, работа неконсервативных сил на замкнутом пути не равна нулю, с ними не связана потенциальная энергия.
Примеры: сила трения скольжения, сила вязкого трения.
Работа силы трения скольжения зависит не от перемещения тела, а от длины пути: A тр = – mNl,и не равна нулю при возвращении тела в исходную точку.
Если на частицу действуют как консервативные, так и неконсервативные силы, то полная механическая энергия этой частицы сохраняться не будет:
dE = d (K + U) = dA неконс. (1.3.59)
Выражение (1.3.59) является математическим выражением закона изменения полной механической энергии:
* Изменение полной механической энергии частицы равно работе всех действующих на нее неконсервативных сил:
Потенциальная энергия системы частиц складывается из собственной потенциальной энергии U соб (энергия взаимодействия частиц системы между собой) и внешней потенциальной энергии U внешн:
U сист = U соб + U внешн,
где
.
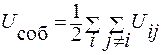Здесь Uij – потенциальная энергия взаимодействия i -той и j -той частиц системы; коэффициент 1/2 учитывает тот факт, что каждое слагаемое в двойной сумме учитывается дважды.
Если на каждую частицу системы действуют, кроме внутренних, также внешние силы, пусть тоже консервативные, то их работа равна убыли внешней энергии dA = – dU внешн,
где 
.
Здесь Ui – потенциальная энергия i -той частицы во внешнем поле. Она зависит от положений всех частиц во внешнем поле и является аддитивной (в отличие от собственной энергии U соб).
В таком случае, полная механическая энергия системы частиц запишется так:
E = K сист + U соб + U внешн.
* Консервативной называется система, полная механическая энергия которой сохраняется: E сист = сonst. В такой системе отсутствуют любые неконсервативные силы (и внешние, и внутренние).
Заметим, что консервативность системы и закон сохранения энергии никак не связаны с замкнутостью системы.
Закон изменения полной механической энергии системы:
* Изменение полной механической энергии системы равно суммарной работе всех неконсервативных сил:
dE сист = dA неконс.
Кинетическая энергия вращающегося вокруг закрепленной оси твердого тела:
, (1.3.60)
где mi – масса i -той частицы, Ri – радиус окружности, по которой вращается i -тая частица, w – угловая скорость вращения тела.
Продифференцируем по времени формулу (1.3.60) и получим закон изменения кинетической энергии вращающегося вокруг закрепленной оси твердого тела:
.
то есть,
* скорость изменения кинетической энергии вращательного движения равна мощности результирующего момента сил относительно оси вращения.
Отсюда
dK вращ = Mzwdt = Mzdj Þ DK º K 2 – K 1 = ò Mzd j,
то есть,
* изменение кинетической энергии вращательного движения равно работе момента сил.
Движение твердого тела, при котором центр масс перемещается в фиксированной плоскости, а ось вращения тела, проходящая через его центр масс, остается перпендикулярной к этой плоскости, называется плоским движением. Типичным примером такого движения является качение симметричного тела.
Это движение можно свести к совокупности поступательного движения и вращения вокруг неподвижной (закрепленной) оси.
Кинетическая энергия тела, совершающего плоское движение, запишется в виде
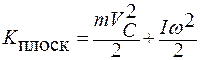. (1.3.61)
Здесь VС – скорость движения центра масс тела.
Пример 22. Однородный диск массы 1 кг и радиуса 1 м катится без трения и проскальзывания. Скорость центра масс диска составляет 1 м/с. Найти кинетическую энергию диска.
Дано: m = 1 кг;
R = 1 м;
VC = 1 м/с.
Найти: К плоск.
Решение. Данное движение диска является плоским, поэтому для кинетической энергии диска запишем формулу (1.3.61):
.
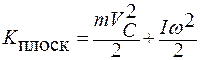Найдем момент инерции диска, вращающегося относительно оси, проходящей через его центр масс из (1.3.52):
IC = (1/2) mR 2,
а угловую скорость вращения диска из (5.17): v = wR.
Имеем:
= 
=
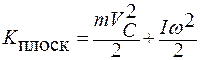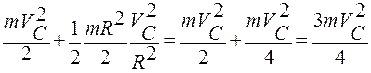= 0,75 (Дж).
Ответ: 0,75 Дж.
Пример 23. Небольшая шайба массы 1 кг, имея начальную скорость 10 м/с, останавливается, пройдя путь, равный 5 м. Найти силу трения, действующую на шайбу.
Дано: m = 1 кг;
V 0 = 1 м/с;
S = 5 м.
Найти: F тр.
Решение. В силу того, что во время движения на шайбу действует сила трения, полная механическая энергия шайбы изменяется, причем из (1.3.59) имеем:
dE = d (K + U) = dA неконс или в интегральной форме, расшифровывая работу силы трения,
DЕ = A неконс = F тр× S × cosa = – F тр× S, (1.3.62)
так как вектор силы трения противонаправлен перемещению шайбы, то есть a = 180°, cos 180° = – 1.
Запишем, чему равно изменение полной механической энергии шайбы, используя (1.3.62):
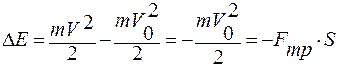, откуда
= 10 (Н).
Ответ: 10 Н.
Пример 24. Резиновая шайба массы 1 кг, двигаясь со скоростью 1 м/с, соскальзывает с горки высотой 1 м и приобретает скорость V у подножия горки. Во время движения над шайбой была совершена работа сил трения А тр = 1 Дж. Считая, что ускорение свободного падения составляет 10 м/с2, найти скорость шайбы V.
Дано: m = 1 кг;
V 0 = 1 м/с;
А тр = 1 Дж;
g = 10 м/с2.
Найти: V.
Решение. Поскольку во время движения шайбы на нее по условию задачи действует сила трения, полная механическая энергия шайбы изменяется. Запишем закон изменения полной механической энергии в интегральной форме:
DE = Е 2 – Е 1 = A тр.
Изменение полной механической энергии:
, откуда выразим скорость, которую приобретает шайба у подножия горки:
= 4,36 (м/с).
Ответ: 4,36 м/с.
Колебания
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости.
В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Свободными или собственными колебаниями называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок, либо она была выведена из положения равновесия. Пример – колебания шарика, подвешенного на нити (маятник). Для того чтобы вызвать колебания можно либо толкнуть шарик, либо, отведя в сторону, отпустить его.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Пример – колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Автоколебания, как и вынужденные, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляется это воздействие, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Пример – часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в те моменты, когда маятник проходит через среднее положение.
При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.
Простейшими являются гармонические колебания, то есть такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса. Этот вид колебаний особенно важен, так как
1) колебания в природе и в технике часто имеют характер, очень близкий к гармоническому;
2) периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Система, совершающая колебания, называется осциллятором.
Система, совершающая гармонические колебания, называется гармоническим осциллятором.
Движение тела, совершающего свободные незатухающие колебания под действием силы вида F = – kx (x – смещение тела из положения равновесия), описывается линейным однородным дифференциальным уравнением второго порядка:
, (1.3.63)
где w 0 – собственная частота свободных незатухающих колебаний.
Для шарика массы m, колеблющегося на пружине жесткостью k:
w 0 = (k/m)1/2. (1.3.64)
Общее решение уравнения (1.3.63) имеет вид:
x = Acos (w 0 t +a), (1.3.65)
где А – амплитуда собственных колебаний, (w 0 t +a) – фаза колебаний, a – начальная фаза колебаний (значение фазы в момент времени t = 0).
Амплитудой колебания называется величина наибольшего отклонения системы от положения равновесия. Амплитуда А – постоянная положительная величина. Ее значение определяется величиной первоначального отклонения или толчка, которым система была выведена из положения равновесия.
Период колебаний Т – это время одного полного колебания:
T = 2 p/w 0. (1.3.64)
Число колебаний в единицу времени – частота колебания n:
n = 1/ T.
За единицу частоты принимается частота такого колебания, период которого равен 1 секунда. Эту единицу называют герцем (Гц).
Из формулы (10.4) для периода Т следует, что
w 0 = 2 p / T,
то есть, w 0– число колебаний за 2 p секунд. w 0 – круговая (циклическая) частота.
В механике гармонические колебания возникают при выполнении следующих условий:
* На частицу (систему частиц) должны действовать сила или момент сил, пропорциональные смещению частицы из положения равновесия и стремящиеся вернуть ее в положение равновесия (квазиупругая сила).
Математический маятник – это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошее приближение к математическому маятнику – небольшой тяжелый шарик, подвешенный на длинной тонкой нитке.
Физический маятник – это любое физическое тело, совершающее колебания вокруг оси подвеса, не проходящей через центр масс, в поле сил тяжести.
Уравнение колебаний математического и физического маятников имеет вид:
.
Оно идентично уравнению колебаний шарика на пружине. Его решение:
j = Acos (w 0 t +a),
то есть, при малых колебаниях угловое отклонение математического и физического маятников изменяется со временем по гармоническому закону.
Период колебаний математического маятника:
T = 2 p / w 0 = 
,
где l – длина нити математического маятника, g – ускорение свободного падения.
Период колебаний физического маятника:
,
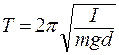где I – момент инерции маятника, m – масса маятника, g – ускорение свободного падения, d – расстояние от точки подвеса до центра масс маятника.
Если система совершает свободные затухающие колебания (в вязкой среде, где на нее будут действовать силы вязкого трения или силы сопротивления среды) 
, то уравнение движения системы будет иметь вид:
.
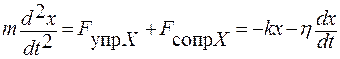Обозначим: k / m = w 02, h /2 m = b, тогда получим д инамическое уравнение собственных затухающих колебаний в общем виде:
. (1.3.67)
Если b < w 0 (сопротивление среды невелико), то колебания осциллятора совершаются по закону
x (t) = A 0 e–btcos (wt+a), (1.3.68)
где А (t) = A 0 e–bt – амплитуда затухающих колебаний, убывающая по экспоненциальному закону, w – собственная частота затухающих колебаний, причем
. (1.3.69)
Такое уменьшение амплитуды А называют релаксацией (ослаблением колебаний), а коэффициент b – коэффициентом затухания колебаний.
t – время релаксации – время, за которое амплитуда A (t) уменьшается в е = 2,71828 раз.
t = 1/ b. (1.3.70)
Логарифмический декремент затухания – это натуральный логарифм отношения амплитуд (или смещений) через период:
. (1.3.71)
Период затухающих колебаний:
.
Если сопротивление среды велико (b ³ w 0), то общее решение уравнения собственных затухающих колебаний будет иметь вид:
x (t) = A 1 el 1 t + A 2 el 2 t.
(сумма двух убывающих экспонент).
x
A 0
t
При возвращении осциллятора в положение равновесия никаких колебаний не возникает, и такое движение осциллятора называется апериодическим (см. рис).
Полная механическая энергия осциллятора складывается из потенциальной энергии, обусловленной наличием консервативной квазиупругой силы Fx = – kx и равной
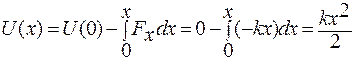(1.3.72)
и кинетической энергии 
.
Если осциллятор вращается, то его кинетическая энергия заменяется на 
.
* Полная механическая энергия гармонического осциллятора всегда пропорциональна квадрату амплитуды его колебаний:
E = K+U = (kA 2/2) = const. (1.3.73)
Если на колеблющуюся систему (одномерный осциллятор) действует внешняя сила, изменяющаяся по гармоническому закону F вн = F 0 cos (w вн t), то уравнение движения осциллятора будет иметь вид:
, (1.3.74)
– это динамическое уравнение вынужденных колебаний.
Здесь b = h /2 m – коэффициент затухания, w 0 = (k / m)1/2 – собственная частота незатухающих колебаний, F 0 – амплитуда внешней вынуждающей силы, w вн – частота внешней вынуждающей силы.
Вынужденные колебания с частотой внешней силы w вн останутся после того, как собственные колебания затухнут. Поэтому для такого установившегося со временем режима колебаний решением уравнения (1.3.74) будет частное решение в виде гармонической функции
x (t) = Acos (w вн t – a),
где А – амплитуда вынужденных колебаний, a – отставание по фазе от вынуждающей силы, которые соответственно равны:
;
.
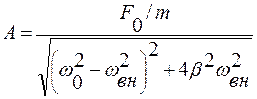* Установившиеся вынужденные колебания происходят с постоянной, не зависящей от времени амплитудой, то есть, не затухают, не смотря на сопротивление среды, поскольку работа внешней силы идет на увеличение механической энергии осциллятора и полностью компенсирует ее убывание, которое происходит из-за действия диссипативной силы сопротивления среды.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой:
. (1.3.75)
Амплитуда при резонансе:
.
Пример 25. Тело массы 1 кг, подвешенное на пружине жесткости k, совершает колебания по закону x = 0,5 cos (6,5 t), t измеряется в секундах, x – в метрах. Найти амплитуду колебаний, кинетическую и потенциальную энергию тела при x = 0,16 м, а также полную механическую энергию тела.
Дано: x = 0,5 cos (6,5 t);
x = 0,16 м;
m = 1 кг.
Найти: A, K, U, E.
Решение. а) Амплитуду колебаний найдем из данного в условии задачи динамического уравнения собственных незатухающих колебаний, сравнив его с уравнением (1.3.65):
x = Acos (w 0 t +a), x = 0,5 cos (6,5 t),
где А – амплитуда колебаний. Очевидно, что А = 0,5 (м).
Из этого же уравнения видно, что собственная частота незатухающих колебаний w 0 составляет 6,5 (с–1). Поскольку тело подвешено на пружине, то, следуя (1.3.64), запишем:
w 0 = (k/m)1/2, откуда выразим коэффициент жесткости пружины:
k = w 02× m. (1.3.76)
б) Найдем кинетическую энергию тела при смещении из положения равновесия на величину x = 0,16 м. Из (1.3.57) следует, что
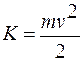, (1.3.77)
где v – скорость тела в тот момент, когда смещение тела из положения равновесия составляет 0,16 м. Найдем эту скорость, учитывая (1.3.22):
= – 0,5×6,5× sin (6,5 t). (1.3.78)
Момент времени t в (1.3.78), который соответствует смещению тела из положения равновесия x = 0,16 м, найдем из динамического уравнения собственных незатухающих колебаний x = 0,5 cos (6,5 t):
0,5 cos (6,5 t) = 0,16 Þ t = [ arccos ((0,16/0,5)]/6,5 = 0,19 (с).
Замечание. arccos ((0,16/0,5) = 71,34°, градусы необходимо перевести в радианы: 71,34° = 1,245 (рад). Тогда t = 1,245/6,5 =
= 0,19 (с).
Подставим найденное время в (1.3.78), а затем из (1.3.77) найдем кинетическую энергию колеблющегося тела:
= – 0,5×6,5× sin (6,5 t) = – 0,5×6,5× sin (6,5×0,19) = – 3,08 (м/с),
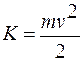= 4,74 (Дж).
в) Потенциальная энергия тела, совершающего гармонические колебания на пружине, согласно (1.3.72) и (1.3.76), равна
= (w 0× m × x 2)/2 = 0,54 (Дж).
г) Полную механическую энергию тела найдем из (1.3.73):
E = K+U = (kA 2/2) = 5,28 (Дж).
Ответ: 0,5 м; 4,74 Дж; 0,54 Дж; 5,28 Дж.
Пример 26. Дифференциальное уравнение собственных гармонических колебаний имеет вид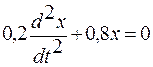 
. Найти собственную частоту и период этих колебаний.
Дано: .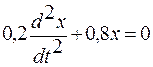
Найти: w 0, Т.
Решение. Преобразуем данное в условии задачи уравнение к виду (1.3.63), для чего разделим его почленно на 0,2:
, откуда w 02 = 4, w 0 = 2 (с–1).
Период колебаний найдем из (1.3.660.4):
T = 2 p/w 0 = 3,14 (с).
Ответ: 2 с–1; 3,14 с.
Пример 27. Рассматривая ногу как физический маятник, определить период колебаний, пользуясь формулой для физического маятника 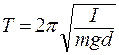. Ногу считать стержнем длиной 0,8 м с шарниром на конце, центр тяжести находится на расстоянии 0,5 м от ступни. Масса ноги 12 кг.
Дано: m = 12 кг;
l = 0,8 м;
d = 0,5 м.
Найти: Т.
Решение. Момент инерции ноги находим по формуле для момента инерции стержня длины l (см. пример 18):
I = ml 2/3,
тогда для периода колебаний получим:
(с).
Ответ: 1,7 с.
Пример 28. Дифференциальное уравнение затухающих колебаний имеет вид 
. Найти коэффициент затухания и собственную частоту этих колебаний.
Дано: .
Найти: w, b.
Решение. а) Найдем коэффициент затухания колебаний, для чего сначала приведем уравнение, данное в задаче, к виду (1.3.67), разделив его почленно на 0,5:
, откуда видно, что 2 b = 0,5 и b = 0,25 (с–1).
б) Из этого же уравнения находим, что
w 02 = 16, тогда w 0 = 4 (с–1).
Собственная частота затухающих колебаний, как следует из (1.3.69), равна
= (16 – 0,0625)1/2 = 3,99 (с–1).
Ответ: 0,25 с–1; 3,99 с–1.
Пример 29. Грузик массой 1 кг совершает колебания на пружине жесткостью 2 Н/м по закону x (t) = A 0 e–аtcos (bt+p /4). Найти а) коэффициент затухания (b = 1 с–1); б) логарифмический декремент затухания (b = 1 с–1); в) собственную частоту затухающих колебаний (а = 1 с–1).
Дано: x (t) = A 0 e–аtcos (bt+p /4);
m = 1 кг;
k = 2 Н/м;
а = 1 с–1;
b = 1 с–1.
Найти: b, l, w.
Решение. а) Сравним данное в условии задачи динамическое уравнение затухающих колебаний с уравнением (1.3.68):
x (t) = A 0 e–btcos (wt+a), x (t) = A 0 e–аtcos (bt+p /4), откуда
b = w – собственная частота затухающих колебаний;
b = а – коэффициент затухания.
Собственная частота незатухающих колебаний, согласно (1.3.64) и (1.3.69):
w 0 = (k/m)1/2 = (w 2 + b 2) = (b 2 + b 2) Þ b = ((k/m) – b 2)1/2 = 1 (с–1).
б) Логарифмический декремент затухания найдем их (1.3.71):
l = bТ = 2 pb / w = 2 pb / b = 6,28.
в) По условию задачи а = 1 (с–1), причем b = а. Поэтому, как следует из (1.3.69),
w = (w 02 – b 2) = ((k/m) – а 2)1/2 = 1 (с–1).
Ответ: 1 с–1; 6,28; 1 с–1.
Пример 30. За 5 секунд амплитуда колебаний уменьшается в «е» раз. Найти коэффициент затухания колебаний.
Дано: t = 5 с.
Найти: b.
Решение. По условию задачи известно время релаксации колебаний t – время, за которое амплитуда колебаний уменьшается в «экспоненту» раз. Согласно (1.3.70), имеем:
t = 1/ b = 1/5 = 0,2 (с–1).
Ответ: 0,2 с–1.
Пример 31. Уравнение вынужденных колебаний имеет вид 
. Найти частоту внешней вынуждающей силы, собственную частоту незатухающих колебаний и резонансную частоту.
Дано: ;
Найти: а) w вн; б) w 0; в) w рез.
Решение. а) Для того, чтобы найти частоту внешней вынуждающей силы, приведем уравнение, данное в условии задачи, к виду (1.3.74), для чего разделим уравнение на 0,4:
,
откуда видно, что
а) w вн = 3 (с–1);
б) w 0 = 2 (с–1).
в) Резонансную частоту найдем из (1.3.75):
,
причем 2 b = 1,2 (как следует из уравнения колебаний), и b = 0,6 (с–1).
Тогда = (22 – 2(0,6)2)1/2 = 1,81 (с–1).
Ответ: 3 с–1; 2 с–1; 1,81 с–1.
