Основные способы формирования выборочной совокупности

Способ отбора - порядок отбора единиц из генеральной совокупности. Различают два вида:

1) повторный;

2) бесповторный.

Повторный отбор - отобранную единицу после обследования возвращают в генеральную совокупность, и она снова участвует в отборе. Численность генеральной совокупности при этом все время остается неизменной, а вероятность попадания каждой единицы в выборку постоянной.

Бесповторный отбор - отобранные однажды единицы в генеральную совокупность не возвращаются. Вероятность попадания отдельных единиц в вы­борку увеличивается по мере производства отбора.

В зависимости от методики формирования выборочной совокупности различают следующие виды выборки.

Простая случайная выборка - отбор, при котором единицы отбираются из генеральной совокупности наудачу. Этот выбор осуществляется двумя путями: жеребьевкой; с помощью таблиц случайных чисел.

Механическая выборка - вид отбора, при котором наблюдению подвергаются единицы, равно отстоящие друг от друга (отбирается каждая пятая единица, каждая десятая). Если единицы генеральной совокупности располагаются в случайном порядке, не зависящем от изучаемого признака, механическая выборка называется несистематической. Если единицы генеральной совокупности расположены в порядке увеличения или уменьшения изучаемого признака, механическая выборка называется систематической.

При механической выборке учитывается шаг отсчета и начало отсчета. Шаг отсчета - расстояние между соседними отбираемыми единицами. Он определяется делением численности генеральной совокупности на объем выборки h = N /n. Начало отсчета - номер единицы, которая должна быть отобрана первой.

Типическая выборка применятся для совокупности, не являющейся однородной по изучаемому признаку. При этом генеральную совокупность раз­бивают на однородные группы (типы) по изучаемому признаку. Затем из каждой группы отбирается определенное число единиц.

При пропорциональной выборке из каждой группы отбирают число единиц, пропорциональное удельному весу данной группы в генеральной совокупности. Стандартная ошибка непропорциональной выборки зависит от величины средней из групповых дисперсий .

Серийная выборка - из генеральной совокупности отбираются не единицы, подлежащие обследованию, а группы (серии, гнезда) единиц. Стандартные ошибки выборки при серийном отборе зависят от величины межсерийной дисперсии, которая оп­ределяется по формуле:

где ^~ - межсерийная дисперсия выборочной совокупности;

r - число отобранных серий. Предельная ошибка серийной выборки:

Комбинированная выборка - комплексное использование нескольких видов выборки. Величина стандартной ошибки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле:

Где ₁ и ₂ - стандартные ошибки соответственно механической и типической выборок.

 

№9.Виды относительных величин.

Относительные статистические показатели более объективно выражают количественные соотношения между явлениями. Для ана­лиза здоровья населения и деятельности системы здравоохранения выделяют следующие:

экстенсивные показатели; интенсивные показатели; показатели соотношения; показатели наглядности.

Экстенсивные показатели показывают внутреннюю структуру явления, распределение его на составные части, удельный вес каж­дой части в целом и выражаются в процентах (%). Эти показатели дают возможность сопоставлять структуры одной и той же совокуп­ности в различные моменты времени, делать выводы о тенденциях и закономерностях структурных изменений в динамике. К экстенсивным показателям относятся структура заболеваемости, инвалидно­сти, смертности, коечного фонда, врачебных специальностей и др.

В то же время на основании экстенсивных показателей нельзя судить о частоте изучаемого явления и динамике его во времени. Для этой цели всегда необходимо знать численность среды, в которой происходят явления, и вычислять интенсивные показатели. Часть явления Х 100%

Целое явление

Интенсивные показатели характеризуют уровень, распростра­ненность какого-либо явления в среде, которое непосредственно связано с этой средой. Эти показатели рассчитывают, как правило, для анализа здоровья населения, где в качестве среды берут числен­ность населения, а в качестве явления — число рождений, заболева­ний, смертей и др., которые выражают в промилле (%о), децимилле (%оо), сантимилле (%ооо). К интенсивным показателям относятся по­казатели заболеваемости, рождаемости, смертности населения и др. Эти показатели в отдельности можно сравнивать на различных адми­нистративных территориях, группах населения, наблюдать на дан­ный момент времени или в динамике.

Интенсивные показатели могут быть общими и специальными. Общие показатели характеризуют явление в целом, например, общие коэффициенты рождаемости, смертности, заболеваемости, вычис­ленные ко всему населению субъекта РФ, города, района и др.; пока­затель больничной летальности, рассчитанный на всех выбывших из стационара больных. Эти показатели позволяют оценить динамику явления или процесса в самом общем виде. Для более углубленного и дифференцированного анализа явлений необходимо пользоваться специальными интенсивными показателями. Особенностью специ­альных показателей является уточнение группировки. Например, при вычислении специальных коэффициентов рождаемости (плодо­витости) за среду берется не все население, а только женщины в воз­расте 15—49 лет. Или другой пример: для углубленного анализа мла­денческой смертности рассчитываются коэффициент ранней неона-тальной смертности (смертность детей в первые 7 суток, т.е. в первые 168 часов жизни), коэффициент поздней неонатальной смертности (смертность детей в возрасте 8—28 суток жизни) и др.» Явление Х (100, 1000, 10000 и т.д.)‏

Среда, продуцирующая данное явление

 

Показатели соотношения характеризуют уровень (распростра­ненность) какого-либо явления в среде, непосредственно (биологи­чески) не связанного с этой средой. В этом их отличие от интенсивных показателей. Показатели соотношения рассчитывают, как пра­вило, для анализа деятельности системы здравоохранения, ее ресурс­ного обеспечения, где в качестве среды берут численность населения, а в качестве явления — число врачей, средних медицинских работни­ков, больничных коек, посещений амбулаторно-поликлинических учреждений и др., и выражают в промилле (%с), децимилле (%оо), сантимилле (%ооо). К показателям соотношения относятся обеспе­ченность населения стационарной, амбулаторно-поликлинической помощью, врачами, средними медицинскими работниками и др. Эти показатели, так же как и показатели интенсивности, можно сравни­вать на различных административных территориях, изучать на дан­ный момент времени или в динамике. Явление Х (100, 1000, 10000 и т.д.)‏

Среда, непродуцирующая данное явление

 

Показатели наглядности применяют для анализа степени изме­нения изучаемого явления во времени. Они указывают, на сколько процентов или во сколько раз произошло увеличение или уменьше­ние сравниваемых показателей за данный период времени. Показа­тели наглядности получают при отношении ряда сравниваемых ве­личин к исходной величине, принятой за 100 или за 1. Как правило, за такую исходную величину берут начальные или конечные значе­ния временного ряда. По сути, эти показатели являются базисными темпами роста, применяемыми для анализа временных рядов.

Показатели наглядности являются одной из разновидностей ин­дексов, широко используемых в статистике.

 

№10.Динамические ряды

Динамический ряд — ряд однородных величин, характеризующих изменения явления во времени

Область применения.

• для характеристики изменений состояния здоровья населения в целом или отдельных его групп, а также деятельности учреждений здравоохранения и изменения их во времени;
• для установления тенденций и закономерностей изменений явлений, углубленного анализа динамического процесса (скоростей, временных характеристик текущего и стратегического планирования;
• для прогнозирования уровней явлений общественного здоровья и здравоохранения

Числа (уровни) динамического ряда. Динамические ряды могут быть представлены только однородными величинами: абсолютными, относительными или средними величинами

 

Виды динамических рядов

1.По времени. В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. (наличие тракторов на 1 января, численность населения на 1 января)

Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. (прибыль 1 кв. + П(2кв) + П(3кв) + П(3кв) = прибыль за год)

Ряды с нарастающими итогами - при составлении таких рядов производится последовательное суммирование смежных уровней.

2. По форме представления уровней. Могут быть построены ряды динамики, уровни которых представляют собой абсолютные, относительные и средние величины. (динамический ряд прибыли, рентабельности, средняя прибыль по району).

3. По расстоянию между датами (интервалам времени) выделяют:

Полные ряды динамики (равноотстоящие ряды) имеют место тогда, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами.

Неполныеряды динамики – когда принцип равных интервалов не соблюдается.

4. По числу показателей выделяют:

Изолированный ряд динамики (одномерный) – имеют место, когда ведется анализ во времени одного показателя.

Комплексный ряд динамики (многомерный) получается в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления.

Расчет показателей динамич.ряда:

Базисные - показатели, при расчете которых каждый уровень сравнивается с одним и тем же уровнем, именуемым базисным.

Цепные - показатели, при расчете которых последующий уровень сравнивается с предыдущим.

 

Наименование показателя	Цепной	Базисный	Интерпретация
Абсолютный прирост			показывает, насколько данный уровень ряда превышает уровень, взятый за базу сравнения
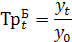
Темп роста			показывает во сколько раз изменился текущий уровень относительно базисного уровня
Темп прироста		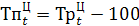	показывает на сколько % изменился сравниваемый уровень относительно базисного уровня

_t - абсолютный прирост данного уровня;

y_t-1 - базисный уровень (уровень предыдущего периода);

Y0 - значение базисного уровня ряда динамики.

№11.Средние величины

Средняя величина - обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность. Средние величины получаются из вариационных рядов.

Виды средних величин:

М - Среднее арифметическое –общая мера исследуемого признака в совокупности. Особенности взвешенной средней (пример со средним количеством дней госпитализации в разных больницах, пример с процентным соотношением курящих на разных факультетах).

Мо - Мода –величина наиболее часто встречаемая в вариационном ряду (определяет пик графика).

Ме - Медиана – величина, занимающая в вариационном ряду срединное положение (медиана необходима для определения нормальности распределения признака в вариационном ряду). Рассчитывается только в ранжированном вариационном ряду.

 

Простая сред. арифметическая

 

 

1) Взвешенная сред. арифметич.

2)Сред.арифметич. по способу моментов

 

 

А – условная средняя

i – величина интервала

a – условное отклонение от условной средней (a = V - A)‏

p – частота

 

Показатели вариации:

Лимит (lim) ‏

Амплитуда (Amp) ‏

Среднее квадратичное отклонение - отклонение отражает вариабельность признака и зависит от распределения вариант в совокупности.

 

Коэффициент вариации: вариационный ряд считается однородным при С_V>10%, обладающим средней вариабельностью признака при С_V=10-20% и высокой вариабельностью при С_V>20%