Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.
Существует несколько эквивалентных формулировок первого начала термодинамики
В любой изолированной системе запас энергии остаётся постоянным.[2] Это — формулировка Дж. П. Джоуля (1842 г.).
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщённому системе, в сумме с изменением энергии, связанной сколичеством вещества N при химическом потенциале μ, и работы A '[3], совершённой над системой внешними силами и полями, за вычетом работы A, совершённой самой системой против внешних сил
Δ U = Q − A + μΔ N + A '.
Для элементарного количества теплоты δ Q, элементарной работы δ A и малого приращения dU внутренней энергии первый закон термодинамики имеет вид:
dU = δ Q − δ A + μ dN + δ A '.
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.
Важно заметить, что dU и dN являются полными дифференциалами, а δ A и δ Q — нет.
Частные случаи
1. Если δ Q > 0, то это означает, что тепло к системе подводится.
2. Если δ Q < 0, аналогично — тепло отводится.
3. Если δ Q = 0, то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.
Первое начало термодинамики:
§ при изобарном процессе
§ при изохорном процессе (A = 0)
§ при изотермическом процессе (Δ U = 0)
Здесь 
— масса газа, 
— молярная масса газа, 
— молярная теплоёмкость при постоянном объёме, 
— давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.
Адиабатические процессы
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.Серьёзное исследование адиабатических процессов началось в XVIII веке.
Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы.
Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на какой-либо термодинамической диаграмме, называется адиабатой. Существует ряд явлений природы, которые могут считаться адиабатическим процессом, кроме того, он получил применение в технике.
Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена (Δ Q = 0) системы со средой сводится только к последним двум процессам[5]. Поэтому, первое начало термодинамики в этом случае приобретает вид:
,
где 
— изменение внутренней энергии тела, 
— работа, совершаемая системой, 
— теплота, полученная системой.
Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит
Уравнение Пуассона
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает
§ электростатическое поле,
§ стационарное поле температуры,
§ поле давления,
§ поле потенциала скорости в гидродинамике.
Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.
Это уравнение имеет вид: Δφ = f,
где Δ — оператор Лапласа или лапласиан, а f — вещественная или комплексная функция на некотором многообразии.
В трёхмерной декартовой системе координат уравнение принимает форму:
В декартовой системе координат оператор Лапласа записывается в форме 
и уравнение Пуассона принимает вид:
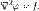
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):
Δφ = 0.
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».
