Построение проекции фигуры сечения начинается с определения характерных точек.
1. Самую высокую и самую низкую точки определяем для того, чтобы знать, в каких пределах вводить вспомогательные плоскости.
2. Граничная точка для определения границы видимости сечения.
3. Самую близкую и самую удаленную от нас точку.
Пример7.. Построить сечение конуса плоскостью общего положения (плоскость может быть задана следами или пересекающимися прямыми), рисунок 8.
Представление поверхностей вращения, как многогранников с бесчисленным числом сторон, приводит к мысли о том, что сечение поверхности вращения плоскостью может быть получено аналогично построениям сечения многогранников.
Сечением такого цилиндра плоскостью будет эллипс, в случае прохождения плоскости через ось вращения вырожденный (две параллельные прямые).

Рисунок 8.23 - Сечение цилиндра плоскостью общего положения
Рассмотрим возможность построения сечения проецирующего цилиндра
плоскостью общего положения Р (рисунок 8.23). В силу начальных условий, одна проекция сечения уже определена (11,…, 121). В этом случае задача сводится к отысканию точек сечения, лежащих на поверхности цилиндра.
Большая ось эллипса лежит в горизонтально проецирующей плоскости Q
(Q1⊥P1), проходящей через ось вращения.

Рисунок 8.24 – Сечение конуса плоскостью общего положения
Промежуточные точки определятся во вспомогательных плоскостях (Ri) перпендикулярных оси вращения.
Сопряженная ”малая” ось эллипса 56 может быть получена в плоскости R, проходящей через точку О, середину отрезка 12 (большая ось эллипса).
В общем случае промежуточные точки могут быть найдены и другим способом.
Подводя итог рассмотренным решениям, можно отметить, что линии пересечения строятся по точкам, которые на поверхности можно зафиксировать, введя дополнительные плоскости. Этот подход и определяет общую методику построения линии пересечения поверхностей.
Взаимное пересечение поверхностей
Способ секущих плоскостей
Этот способ применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере пересечения цилиндра ∆ и конуса Ф рисунок 8.25.
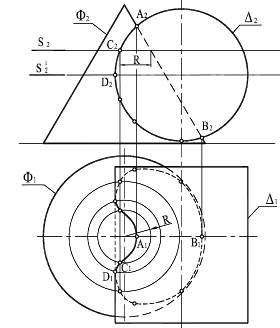
Рисунок 8.25 – Метод секущих плоскостей
Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня Si. На поверхности конуса (в силу того, что они перпендикулярны оси вращения) эти плоскости выделяют окружности, а на поверхности цилиндра - параллельные прямые (образующие).
Характерные точки А, В линии пересечения определяют в пересечении фронтальных очерков. Текущие точки линии пересечения определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях Si.
Способ секущих сфер
Этот способ базируется на том, что две соосные поверхности вращения пересекаются по окружности, лежащей в плоскости, перпендикулярной общей оси вращения.
Сфера будет соосна с любой поверхностью вращения, если ее центр лежит на оси вращения этой поверхности (рисунок 8.26). Это и определяет возможность использовать сферу в качестве вспомогательной секущей поверхности.
Метод секущих сфер применяют в следующих случаях:
1.рассматривают поверхности вращения, их оси должны пересекаться в одной точке - центре секущих сфер.При этом желательно, чтобы плоскость, образованная пересечением осей, была бы параллельна одной из плоскостей проекции.
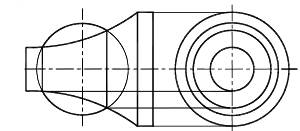
Рисунок 8.26 – Пересечение соосных поверхностей
Линия пересечения двух цилиндров Ф и ∆ (RФ>R∆) может быть определена с помощью метода секущих сфер. Это определяется тем, что выполняются все постав ленные выше условия. Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (рисунок 8.27). Фронтальные проекции характерных точек линии пересечения 12 и 22 определятся в результате пересечения фронтальных очерков Ф2 и ∆2,а горизонтальные определятся по принадлежности этих точек цилиндру Ф.
Низшая точка линии пересечения (3) определяется введением
сферы RФ, которая пересечет цилиндр Ф по окружности l (фрон-
тальная проекция этой окружности совпадет с фронтальной про-
екцией оси вращения цилиндра ∆).

Рисунок 8.27 – Метод секущих сфер
С цилиндром ∆ эта же сфера пересечется по окружности m. Точка 3 и Сфера 1 есть результат пересечения окружностей l и m. Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении произвольных сфер RФ<Ri<О212 с цилиндрами Ф и ∆. Фронтальные проекции точек линии пересечения определяются как пересечения отрезков прямых, в которые вырождаются окружности, перпендикулярные оси вращения, а горизонтальные проекции находятся по принадлежности одной из поверхностей. В данном случае - поверхности Ф.






