Определение натуральной величины фигуры сечения

Так как фигуры сечения принадлежат плоскости сечения, то проще всего определить ее натуральную величину методом вращения плоскости сечения вокруг следа до совмещения с плоскостью проекций, в которой расположен этот след. Фигура сечения, расположенная в плоскости, изображается без искажения. Этот случай вращения называется «способом совмещения».

Пример 4. Совместить плоскость Р с плоскостью П₁ вращением вокруг сле­да P₁, рисунок 6.

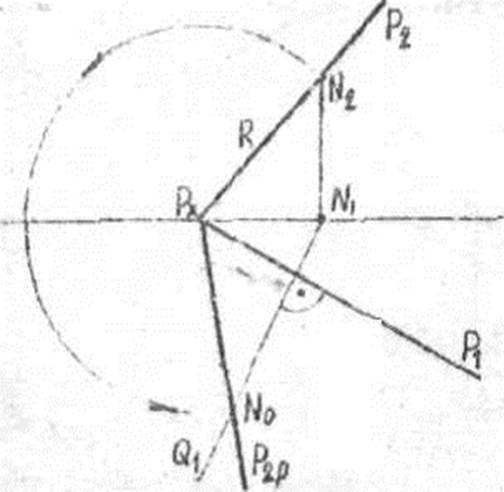
Рисунок 6

Построение выполняем аналогично повороту плоскости вокруг ее горизонтальной или фронтальной линии уровня.

След плоскости можно рассматривать как «нулевую горизонталь».

Чтобы найти совмещенное положение следа Р₂ на плоскости П₁ необходимо:

1.Выбираем любую точку, например N (N₁ N₂) на следе Р₂.

2.При вращении плоскости Р вокруг следа Р1 точка N, будет вращаться в плос­кости Q P (Q₁ P₁). Отметим след плоскости вращения для точки N (Q₁).

3.Из Р_х, как из центра радиусом Р_х N₂ на следе Q₁ делаем засечку - получаем точку N₀.

4.Совмещенный след P2,0 пройдет через неподвижную точку Рх и N0.

 

Пример 5. Определить истинную величину треугольника АВС расположенного в плоскости Р общего положения, рисунок 6. Точки А,В,С лежат на горизонталях плоскости Р.

1.Определяем положение совмещенного следа Р2,0. (см. пример 4).

2.Через точку А проводим след плоскости вращения Σ1 ┴ Р1 точка А€ h.

3. Из Рх, как из центра радиусом Рх М2 отмечаем совмещенное положение следа горизонтали М0.

4. Через точку М₀ проводим совмещенную горизонталь h₀ //P1 до пересечения со следом плоскости вращения Σ1 – получим совмещенную точку А0.

Аналогично определяем положение точек В и С. Соединяем их между собой. А0В0С0 – натуральная величина треугольника.

Пример 6. Определить сечение четырехгранной призмы плоскостью, заданной параллельными прямыми а //б (Рис.7).

 

 

 

Рисунок 7

 

СЕЧЕНИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ ПЛОСКОСТЬЮ.

 

I. Цель работы.

1. Изучение способов построения линии пересечения поверхности вращения и плоскости.

2. Изучение методов определения натуральной величины фигуры сечения.

3. Изучение способов построения развертки поверхностей вращения.

II. Оформление работы.

После того, как задание выполнено в тонких линиях, его проверяет преподаватель. Затем с учетом видимости задание следует обвести соответствующими линиями. Секущая плоскость считается прозрачной.

III. Содержание задания.

1. Построить фигуру сечения данной поверхности вращения и плоскости на плоскостях проекций.

2. Определить истинную величину фигуры сечения.

3. Построить полную развертку усеченной части поверхности вращения.