График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Асимптоты графика функции.
Асимптоты функции
Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
Вертикальные асимптоты
Вертикальные асимптоты определяются точками разрыва функции и границами области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
Вертикальные асимптоты определяются точками разрыва второго рода
В этом случае f(x0 ± 0) = ± ∞, или f (x0 ± 0) = + ∞, или f (x0 ± 0) = − ∞.
Следует отметить, что в этом случае может отмечаться всё разнообразие поведения функции в окрестности точки разрыва. Например, на рис. 8.2 приведён график элементарной функции
Горизонтальные асимптоты
Если
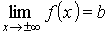 ,
,
то у = b — горизонтальная асимптота кривой y = f (x) (правая – при х стремящемуся к плюс бесконечности, левая – при х стремящемуся к минус бесконечности и двусторонняя, если пределы при х стремящемуся к плюс-минус бесконечности равны).
Наклонные асимптоты
Уравнение наклонной асимптоты функции y = f (x)
Неопределенный интеграл. Определение. Геометрический смысл.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ- интеграл от заданной функции одного переменного, определенной на нек-ром промежутке - совокупность всех первообразных данной функции на этом промежутке.
Геометрический смысл неопределённого интеграла.
Пусть задан неопределённый интеграл F(х) + С для функции f(х) в некотором интервале. При фиксированном значении С = С1 получим конкретную функцию у1 = F(х) + С1, для которой можно построить график; его называют интегральной кривой. Изменив значение С и положив С = С2, получим другую первообразную функцию С соответствующей новой интегральной кривой.
Таблица интегралов. Св-ва неопределенного интеграла.
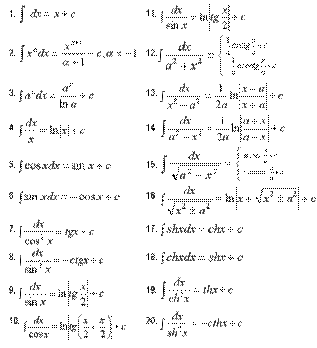
Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если 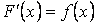 , то
, то

Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
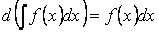
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
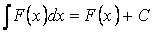
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
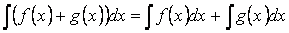
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
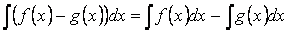
Свойство 6. Постоянный множитель можно выносить за знак интеграла
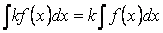
Свойство 7. Если
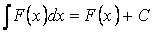
то







