Производная сложной функции.
Сложная функция – это функция, аргументом которой также является функция.
Формула нахождения производной сложной функции.
8. Уравнение касательной. Уравнение нормали.
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x 0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [ a; b ].Тогда в любой точке x 0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x 0) · (x − x 0) + f (x 0)
Здесь f ’(x 0) — значение производной в точке x 0, а f (x 0) — значение самой функции.
Уравнение нормали к графику функции f  (x) в точке x 0, при условии, что f ' (x 0) ≠ 0 имеет вид:
|
|
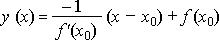
Правило Лопиталя. Условия применения.
ПравилоЛопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 
и 
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1. 
или 
;
2. 
и 
дифференцируемы в проколотой окрестности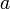 
;
3. 
в проколотой окрестности ;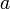
4. существует 
,
тогда существует 
.
Пределы также могут быть односторонними.
Необходимые и достаточные условия возрастания, убывания функции.
Достаточные условия возрастания и убывания функции в точке и на интервале
Теорема. Для того чтобы функция f (x), дифференцируемая в точке х 0 Î (а, b), возрастала (убывала) в точке х 0, достаточно, чтобы f ' (x 0) > 0 (f ' (x 0) < 0).
Доказательство. Так как по условию f (x) дифференцируема в точке х 0 Î (а, b), то существует предел
.
В достаточно малой окрестности точки х 0 имеем
,
где sign A означает "знак выражения А". Для случая f ' (x 0) > 0 имеем sign f ' (x 0) = + 1, поэтому
sign (f (x 0 + h) − f (x 0)) = sign (h).
Откуда следует f (x 0 − h) < f (x 0) < f (x 0 + h), что означает возрастание функции в точке.
Необходимые условия возрастания и убывания функции в точке и на интервале
Теорема. Для того чтобы функция f (x), дифференцируемая в точке х 0 Î (а, b), возрастала (убывала) в точке x 0, необходимо, чтобы её производная в точке х 0 была неотрицательной f ' (x0) ≥ 0 (неположительной f ' (x0) ≤ 0).
Доказательство. Пусть функция f (x) возрастает в точке х 0 Î (а, b) и справедливы неравенства
f (x 0 − h) < f (x 0) < f (x 0 + h)
В этом случае для положительного приращения h имеем
и 
.
Выполняя предельный переход в неравенствах, получим
.
Аналогично
.
Так как функция имеет производную в точке, то
,
что и требовалось доказать.
Определение. Функция f (x) называется строго возрастающей (убывающей) на отрезке [ а, b ], если для любых значений аргументов из этого отрезка большему значению аргумента соответствует строго большее (меньшее) значение функции.
Как следствие теоремы Лагранжа можно сформулировать теорему.
Теорема. Если функция f (x) определена на отрезке [ а, b ], дифференцируема в точках х Î (а, b) и
f ' (x) > 0, (f ' (x) < 0),
то функция f (x) возрастает (убывает) на отрезке [ а, b ].
Доказательство. Применим теорему о конечных приращениях для двух произвольных точек х1 < х2 Î [ а, b ]
f (x 2) − f (x 1) = f ' (c)·(x 2 − x 1),
где с Î (x 1; x 2). Из этого соотношения следует
sign (f (x 2) − f (x 1)) = sign f ' (c)
В случае f ' (x) > 0 для всех х Î (а, b) имеем f (x 2) > f (x 1), и большему значению аргумента соответствует большее значение функции. Что свидетельствует о возрастании функции.
