На наступних сторінках наводяться тексти завдань Д3.1 – Д3.30 з відповідними рисунками та таблицями даних. Величини, які помічені в таблицях знаком питання “? ” потрібно знайти як результат обчислень. Величини, проти яких прочерк “ – “, є такими, що не потрібно визначати, або такими, що для даної задачі не мають практичного змісту.
Теоретичні відомості. Для того, щоб виконати дослідження руху точки під дією сил, використовують диференціальне рівняння руху, яке в проекції на вісь Ох має вигляд.
, (3.1)
де m – маса точки,
х – її координата в вибраній системі координат;
Х – проекція діючої сили на вісь х;
k – порядковий номер сили, k = 1, 2, 3, …
Права частина диференціального рівняння (3.1) є основною тому, що з одної сторони характеризує процес руху як механічне явище, а з другої - впливає на аналітичний вигляд диференціального рівняння як математичної моделі. В даному завданні пропонується дослідити явище руху під дією пружних сил, що залежать від координат, сил залежних від швидкості, що має місце при русі з опором середовища, і збурюючих сил, залежних від часу за гармонічним законом.
Диференціальні рівняння, які отримуються з його загальної форми (3.1) в залежності від перерахованих сил мають вигляд:
, (3.2)
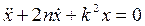, (3.3)
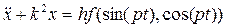. (3.4)
де x = x(t) – шукана функція,
k, n, h, p – постійні величини.
Розв’язком однорідного диференціального рівняння (3.2) є функція
x = C1 sin(kt) + C2 cos(kt). (3.5)
що відповідає вільним гармонічним коливанням.
Для диференціального рівняння (3.3) розв’язок залежить від спів-відношення чисел n і k:
при n > k x = C1 el1t + C2 el2t. (3.6)
при k > n x = e-nt (C1 sin(k1t) +C2 cos(k1t)), (3.7)
при k = n x = e-nt (C1 + C2 t). (3.8)
де l1, l2, k1 – постійні величини, які залежать від k і n,
t – незалежний параметр часу,
С1 і С2 – сталі інтегрування, що залежать від початкових умов.
Функція (3.6) відповідає аперіодичному рухові, (3.7) – затухаючим коливанням і (3.8) – рухові, що є граничним між коливним і аперіо-дичним.
Розв’язком неоднорідного диференціального рівняння (3.4) є сума
x = x* + x** (3.9)
де x* – розв’язок відповідного однорідного диференціального рівняння, який має вигляд функції (3.5),
x** – частинний розв’язок диференціального рівняння (3.4) і має вигляд:
x** = f (B sin(pt), D cos(ht). (3.10)
Тому остаточним розв’язком диференціального рівняння (3.4) є функ- ція вигляду
x = A sin(kt+j) + x**. (3.11)
де A, B, D і j сталі величини, що отримуються як результати обчислень.
Згідно з функцією (3.11) точка здійснює вимушені коливання.
Задача Д3.1
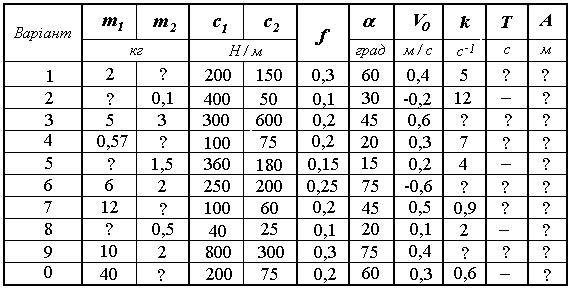
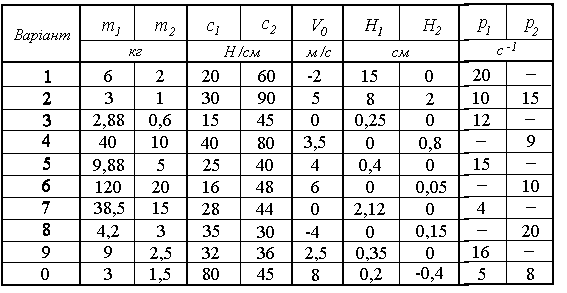
До жорсткого невагомого стержня D, який підвішено до трьох вертикальних пружин жорсткостями с1 і с2, як показано на рис. Д3.1, прикріплено вантаж Р 1, а до нього вантаж Р2. В початковий момент часу вантаж Р2 миттєво від’єднують від вантажа Р1 і надають вантажу Р1 початкової швидкості V0, направленої по вертикалї вниз.
Вважаючи, що стержень D переміщується поступально, знайти рівняння руху вантажа Р1, атакож ті величини, які вказані в таблиці Д3.1, де позначено: А – амплітуда коливань, k – циклічна частота, Т – період коливань. Побудувати графікзалежності координати від часу.
Задані параметри і величини, які потрібно знайти, знаходяться в таблиці Д3.1 по варіантах.
Рисунок Д3.1
Таблиця Д3.1
Задача Д3.2
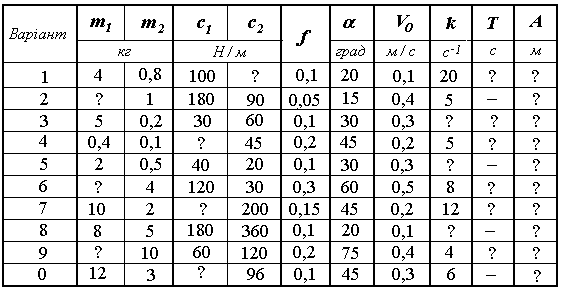
На похилій площині, яка утворює кут a з горизонтом розміщені два вантажі Р1 і Р2, що прикріплені до двох з’єднаних послідовно пружин жорсткостя ми с1 і с2, рис. Д3.2. В деякий моментчасу вантаж Р2 миттєво від’єднують від вантажу Р1 інадають йому початкової швидкості V0, після чого він рухається по площині з якою коефіцієнт тертя рівний f. Знайти рівняння руху вантажу Р1, побудувати графік залежності координати від часу.
Дані для остаточних розрахунків знаходяться в таблиці Д3.2 по варіантах, де позначено m 1, m2 маси грузів Р1 і Р2, відповідно, А – амплітуда коливань, k – циклічна частота, Т – період коливань.
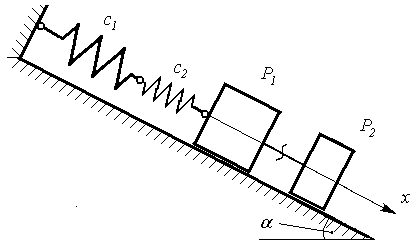
Рисунок Д3.2
Таблиця Д3.2
Задача Д3.3
До невагомого стержня В, який прикріплено до двох пружин жор-сткостями с1 , с2 і демпфера D, підвішено вантажі Р1 і Р2, рис.Д3.3, масами m1, m2 відповідно. В деякий моментчасу вантаж Р2 миттєво від’єднують від вантажу Р1 інадають йому початкової швидкості V0. Визначити рівняння руху вантажу Р1, побудувати графік залежності координати від часу, якщо стржень B рухається поступально, а демпфер D створює силу опору, яка пропорційна швидкості R = m V.
Дані для остаточних розрахунків знаходяться в таблиці Д3.3 по варіа-нтах, де А – амплітуда коливань, k – циклічна частота, Т – період коливань, d – декремент затухаючих коливань.
Рисунок Д3.3
Таблиця Д3.3
Задача Д3.4
До вертикального повзуна В прикріплено послідовно дві пружини жорсткостями с1 і с2, а до них підвішені вантажі Р1 і Р2 масами m1 і m2,відповідно, рис. Д3.4. В деякий моментчасу вантаж Р2 миттєво від’єднують від вантажу Р1, при цьому вантаж Р1 отримує швидкість Vo, а повзун В починає виконувати вертикальний рух за законом
x = H1 sin(p1t) + H2 sin(p2t)
Визначити рівняння руху вантажу Р1 і побудувати графік залеж-ності координати від часу.
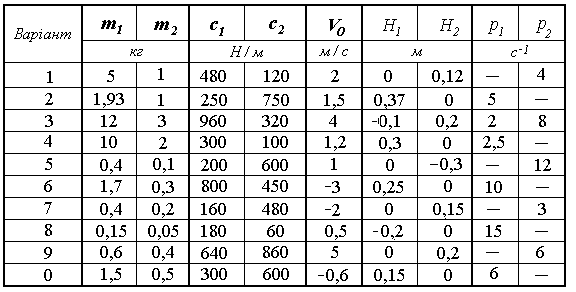
Дані для остаточних розрахунків - в таблиці Д3.4 по варіантах.
Рисунок Д3.4
Таблиця Д3.4
Задача Д3.5
На горизонтальну платформу D1 помістили вантаж Р масою m, який приєднали до системи пружин жорсткостями с 1, с2 і с3, причому на пружину жорсткістю с3 діє в горизонтальному напрямку повзун В, що показано на рис. Д3.5. В деякий моментчасу вантажу Р надають початкову швидкость V0, а повзун В починає виконувати рух за законом
x = H1 sin(p1t) + H2 sin(p2t)
Визначити рівняння руху вантажу Р і побудувати графік залежності координати від часу, якщо тіла D1 і D2 вважаються невагомими, рухаються поступально, а тертя відсутнє.
Дані для остаточних розрахунків - в таблиці Д3.5 по варіантах.
Рисунок Д3.5
Таблиця Д3.5
Задача Д3.6
Тіло Р масою m приєднано до горизонтальних пружин жорст-костями с1, с2 і демпфера D за допомогою невагомого стержня В, як показано на рис. Д3.6. При русі тіла Р демпфер створює силу опору R, яка має напрямок протилежний до швидкості V і описується залежністю R = m V, де m коефіцієнт в’язкості рідини, яка міститься в демпфері. В початковий момент часу тілу Р надають початкову швидкість V0 і зміщення xo, після чого воно виконує рух вздовж горизонтальної осі x.
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо стержень В рухається поступально, відхилення від положення рівноваги малі і горизонтальні.
Дані для остаточних розрахунків знаходяться в таблиці Д3.6 по ва-ріантах, де позначено Т – період затухаючих коливань.
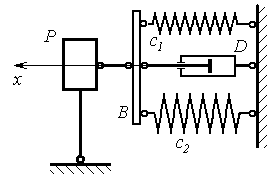
Рисунок Д3.6
Таблиця Д3.6
Задача Д3.7
Тіло Р масою m падає з висоти h на горизонтальну невагому платформу В, яка опирається на пружини жорсткостями с1, с2 і демпфер D, як показано на рис. Д3.7. На висоті h тілу Р надають початкову швидкість U в напрямку вертикалі і воно падає до зустрічі з платформою В. При русі тіла Р разом з платформою демпфер створює силу опору R, яка має напрямок, протилежний до швидкості V і описується залежністю R = m V, де m коефіцієнт в’язкості рідини, яка міститься в демпфері.
Визначити рівняння руху тіла Р і побудувати графік залежності координати від часу, якщо платформа В рухається поступально, а
удар тіла Р до платформи В абсолютно непружний.
Дані для остаточних розрахунків знаходяться в таблиці Д3.7 по варіантах, де Т – період затухаючих коливань.
Рисунок Д3.7
Таблиця Д3.7
Задача Д3.8
На похилій площині з кутом a до горизонту розташований ван-таж Р мaсою m, який закріплено до нижнього кінця послідовно з’єднаних пружин с1 і с2, а до верхнього кінця пружин прикріплено повзун В, що показано на рис. Д3.8. Система знаходиться в поло-женні статичної рівноваги. В деякий момент часу повзун В починає вздовж похилої площини рух за законом
x =H1 sin(p1t) + H2 cos(p2t)
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо коефіцієнт тертя до похилої площини рівний f.
Дані для остаточних розрахунків знаходяться в таблиці Д3.8 по варіантах.
Рисунок Д3.8
Таблиця Д3.8
Задача Д3.9
На похилій площині з кутом a до горизонту розташований ван-таж Р мaсою m, який закріплено до верхнього кінця послідовно з’єднаних пружин с1 і с2 ідо демпфера D, що показано на рис. Д3.9. Система знаходиться в положенні статичної рівноваги. При русі тіла демпфер D створює силу опору залежну від швидкості:
R = m V. В початковий момент часу вантажу Р надають початкове зміщення xo і початкову швидкість Vo, після чого воно рухається
вздовж осі х.
Визначити рівняння руху вантажу Р і побудувати графік залежності координати від часу, якщо коефіцієнт тертя на похилій
площині рівний f.
Дані для остаточних розрахунків - в таблиці Д3.9 по варіантах.
Рисунок Д3.9
Таблиця Д3.9
Задача Д3.10
Два вантажі Р1 і Р2 масами m1 і m2, відповідно знаходяться на невагомій платформі В, яка підтримується системою пружин жорс-ткостями с1, с2 і с3 як показано на рис. Д3.10. Маси вантажів Р1 і Р2 складають відношення: m1/m2 = n, а при вільних коливаннях вка-заних вантажів циклічна частота рівна k. В положенні статичної рівно-ваги платформа В зміщена на lст .
В початковий момент часу вантаж Р2 знімають, при цьому вантаж Р1 набуває початкову швидкість Vo у вертикальному напрямку. Знайти рівняння коливного руху вантажу Р 1, побудувати графік залежності координати від часу, визначити амплітуду (А), період (Т) та початкову фазу (j o), якщо платформа В рухається поступально, а опором середовища нехтуємо.
Дані для остаточних розрахунків - в таблиці Д3.10 по варіантах.
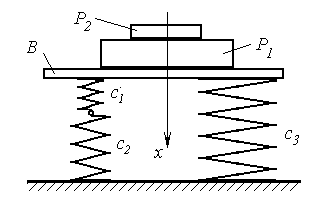
Рисунок Д3.10
Таблиця Д3.10
Задача Д3.11
До жорсткого невагомого стержня D, який підвішено до трьох вер-тикальних пружин жорсткостями с 1 і с2, як показано на рис. Д3.11, прикріплено вантаж Р1. В початковий момент часу до вантажу Р1 миттєво приєднують вантаж Р2 і надають системі вантажів Р1 і Р2 початкову швидкість V0, направлену по вертикалі вниз. Вважаючи, що стержень D переміщується поступально, знайти рівняння руху вантажів Р1 і Р2 як одної точки, атакож ті величини, які вказані в таблиці Д3.11, де позначено: А - амплітуда коливань, k – циклічна частота, Т – період коливань. Побудувати графік залежності коорди-нати від часу.
Задані параметри і величини, які потрібно знайти, знаходяться в таблиці Д3.11 по варіантах.
Рисунок Д3.11
Таблиця Д3.11
Задача Д3.12
На похилій площині, яка утворює кут a з горизонтом, знаходиться вантаж Р1, що прикріплений до двох з’єднаних послідовно пружин жорсткостями с1 і с2, рис. Д3.12. В деякий моментчасу до вантажу Р1 миттєво приєднують вантаж Р2 інадають їм обом початкову швидкість V0, після чого вони рухаються по площині так, що на вантаж Р1 діє сила тертя з коефіцієнтом f, а вантаж Р2 рухається без тертя. Знайти рівняння руху вантажів Р1 і Р2, побудувати графік залежності координати від часу.
Дані для остаточних розрахунків знаходяться в таблиці Д3.12 по варіантах, де m1, m2 маси вантажів Р1 і Р2, відповідно, А – амплітуда коливань, k – циклічна частота, Т – період коливань.
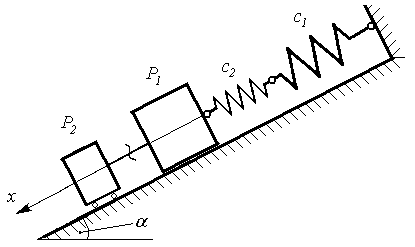
Рисунок Д3.12
Таблиця Д3.12
Задача Д3.13
До невагомого стержня В, який прикріплено до двох пружин жор-сткостями с1 , с2 і демпфера D, підвішено вантаж Р1 масою m1, рис. Д3.13. В деякий моментчасу до вантажу Р1 миттєво приєднуютьвантаж Р2 масою m2 так, що вантажі Р1, Р2 набувають початкову швидкість V0. Визначити рівняння руху вантажів Р1 і Р2, побудувати графік залежності кординати від часу, якщо стржень B рухається пос-тупально, а демпфер D створює силу опору, яка пропорційна швидко-
сті R = m V.
Дані для остаточних розрахунків знаходяться в таблиці Д3.13 по варіантах, де А – амплітуда коливань, k – циклічна частота, Т – період коливань, d – декремент затухаючих коливань.
Рисунок Д3.13
Таблиця Д3.13
Задача Д3.14
До вертикального повзуна В прикріплено пружини жорсткостями с1 і с2, а до них підвішений вантаж Р1 масою m1 , як показано на рис. Д3.14. В деякий моментчасу до вантажу Р1 приєднують вантаж Р2 масою m2, а повзун В починає виконувати вертикальний рух за за-коном
x = H1 sin(p1t) - H2 sin(p2t)
Визначити рівняння руху вантажів Р1, Р2 як одного тіла і побуду-вати гра фік залежності координати від часу, якщо їх початкова швид-кість Vo. Дані для остаточних розрахунків знаходяться в таблиці Д3.14 по варіантах.
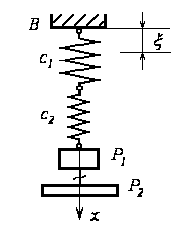
Рисунок Д3.14
Таблиця Д3.14
Задача Д3.15
На невагому платформу D помістили вантаж Р масою m, яка опирається на систему пружин жорсткостями с1, с2 і с3, причому пружина жорсткістю с3 підтримується повзуном В, що показано на рис. Д3.15. В деякий моментчасу вантажу Р надають початкову швидкість V0, а повзун В починає виконувати вертикальний рух за законом
x = H1 sin(p1t) + H2 sin(p2t)
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо в початковий момент часу система знаходилась в положенні статичної рівноваги, платформа D рухається поступально, а тертя відсутнє. Дані для остаточних розрахунків зна-ходяться в таблиці Д3.15 по варіантах.
Рисунок Д3.15
Таблиця Д3.15
Задача Д3.16
Тіло Р масою m приєднано до горизонтальних пружин жорст-костями с1, с2, c3 і демпфера D за допомогою невагомого стержня В, як показано на рис. Д3.16. При русі тіла Р демпфер створює силу опору R, яка має напрямок протилежний до швидкості V і описується залежністю R = m V, де m коефіцієнт в’язкості рідини, яка міститься в демпфері. В початковий момент часу тілу Р надають початкової швидкості V0 і зміщення xo, після чого воно виконує рух вздовж
горизонтальної осі x.
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо стержень В рухається поступально, відхилення від положення рівноваги малі і горизонтальні.
Дані для остаточних розрахунків знаходяться в таблиці Д3.16 по варіантах, де Т – період затухаючих коливань.
Рисунок Д3.16
Таблиця Д3.16
Задача Д3.17
Тіло Р масою m падає з висоти h на горизонтальну невагому платформу В, яка опирається на пружини жорсткостями с1, с2, c3 і демпфер D, як показано на рис. Д3.17. На висоті h тілу Р надають початкову швидкість U в напрямку вертикалі і воно падає до зустрічі з платформою В. При русі тіла Р разом з платформою демпфер ство-рює силу опору R, яка має напрямок протилежний до швидкості V і описується залежністю R = m V, де m коефіцієнт в’язкості рідини, яка міститься в демпфері.
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо платформа В рухається поступа-льно, а удар тіла Р до платформи В абсолютно непружний.
Дані для остаточних розрахунків містяться в таблиці Д3.17 по варіантах, де Т – період затухаючих коливань.
Рисунок Д3.17
Таблиця Д3.17
Задача Д3.18
На похилій площині з кутом a до горизонту розташований вантаж Р мaсою m, який закріплено до верхнього кінця послідовно з’єдна-них пружин с1 і с2, а до нижнього кінця пружин прикріплено повзун В, що показано на рис. Д3.18. Система знаходиться в положенні ста-тичної рівноваги. В деякий момент часу повзун В починає вздовж по-хилої площини рух за законом
x = H1cos(p1t) +H2sin(p2t)
Визначити рівняння руху вантажу Р і побудувати графік залежно-сті координати від часу, якщо коефіцієнт тертя для вантажу Р до по- хилої площини рівний f.
Дані для остаточних розрахунків містяться в таблиці Д3.18 по варі-антах.
Рисунок Д3.18
Таблиця Д3.18
Задача Д3.19
На похилій площині з кутом a до горизонту розташований вантаж Р мaсою m, який закріплено до двох пружин жорсткостями с1 і с2 ідо демпфера D, що показано на рис. Д3.19. Система знаходиться в положенні статичної рівноваги. При русі тіла демпфер D створює силу опору залежну від швидкості: R = m V. В початковий момент часу тілу Р надають початкове зміщення xo і початкову швидкість Vo, після чого воно рухається вздовж осі х.
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо коефіцієнт тертя для вантажу Р до площини рівний f.
Дані для остаточних розрахунків містяться в таблиці Д3.19 по варі-антах.
Рисунок Д3.19
Таблиця Д3.19
Задача Д3.20
Вантаж Р1 знаходиться на невагомій платформі В, яка підтриму-ється системою пружин жорсткостями с1, с2 і с3 як показано на рис. Д3.20. При вільних коливаннях вантажу Р1 циклічна частота рівна k,а в положенні статичної рівноваги платформа В зміщена на lст .
В початковий момент часу на вантаж Р1 кладуть вантаж Р2,при цьому вони набувають початкову швидкість Vo у вертикальному нап-рямку. Маси вантажів Р1 і Р2 складають відношення: m2/m1 = n. Знайти рівняння коливного руху вантажів Р 1 і Р2 як одного тіла, по-будувати графік залежності кординати від часу, визначити амплітуду (А), період (Т) та початкову фазу (j o), якщо платформа В рухає-
ться поступально, а опором середовища нехтуємо.
Дані для остаточних розрахунків містяться в таблиці Д3.20 по варі-антах.
Рисунок Д3.20
Таблиця Д3.20
Задача Д3.21
До жорсткого невагомого стержня D, підвішеного до чотирьох вертикальних пружин жорсткостями с1, с2 і с3, як показано на рис. Д3.21, прикріплено вантаж Р1, а до нього вантаж Р2. В початко-вий момент часу вантаж Р2 миттєво від’єднують від вантажу Р1 і на-дають вантажу Р1 початкову швидкість V0, направлену по вертикалї.
Вважаючи, що стержень D переміщується поступально, знайти рів-няння руху вантажу Р1, атакож ті величини, які вказані в таблиці Д3.21, де позначено: А – амплітуда коливань, k – циклічна частота,
Т – період коливань. Побудувати графік залежності координати від часу.
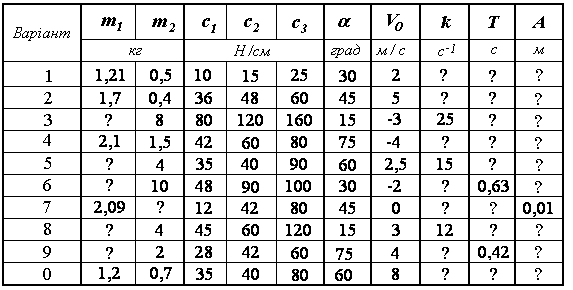
Задані параметри і величини, які потрібно знайти, знаходяться в таблиці Д3.21 по варіантах.
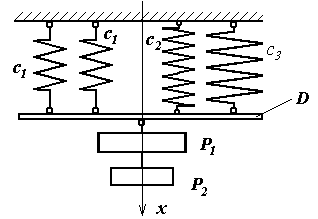
Рисунок Д3.21
Таблиця Д3.21
Задача Д3.22
На похилій площині, яка утворює кут a з горизонтом, розміще-ні два вантажі Р1 і Р2, що прикріплені до системи пружин жорсткос-тями с1, с2 і с3 як показано на рис. Д3.22. В деякий моментчасу ван-таж Р2 миттєво від’єднують від вантажу Р1 інадають йому початко-ву швидкість V0, після чого він рухається по площині, де тертя відсут-нє. Знайти рівняння руху вантажу Р1, побудувати графік залежності координати від часу.
Дані для остаточних розрахунків містяться в таблиці Д3.22 по варі-антах, де m1, m2 маси вантажів Р1 і Р2, відповідно, А – амплітуда коливань, k – циклічна частота, Т – період коливань.
Рисунок Д3.22
Таблиця Д3.22
Задача Д3.23
До невагомого стержня В, прикріпленого до трьох пружин жор-сткостями с1 , с2, с3 і демпфера D, підвішено вантажі Р1 і Р2, рис. Д3.23, масами m1, m2, відповідно. В деякий моментчасу вантаж Р2 миттєво від’єднують від вантажу Р1 інадають йому початкову швидкість V0. Визначити рівняння руху вантажу Р1, побудувати графік залежності координати від часу, якщо стержень B рухається поступально, а демпфер D створює силу опору, яка пропорційна швидкості R = m V.
Дані для остаточних розрахунків знаходяться в таблиці Д3.23 по варіантах, де А – амплітуда коливань, k – циклічна частота, Т – період затухаючих коливань.
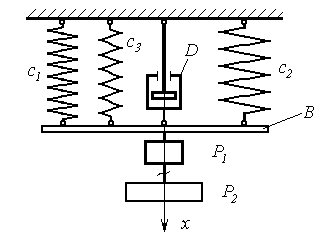
Рисунок Д3.23
Таблиця Д3.23
Задача Д3.24
До вертикального повзуна В прикріплено систему з трьох пружин жорсткостями с1 і с2, а до неї підвішені вантажі Р1 і Р2 масами m1 і m2, відповідно, рис. Д3.24. В деякий моментчасу вантаж Р2 миттєво від’єднують від вантажу Р1, при цьому вантаж Р1 отримує швидкість Vo, а повзун В починає виконувати вертикальний рух за законом
x = H1 sin(p1t) + H2 sin(p2t)
Визначити рівняння руху вантажу Р1 і побудувати графік залежно-сті координати від часу. Масою з’єднувального стержня D нехтуємо.
Дані для остаточних розрахунків - в таблиці Д3.24 по варіантах.
Рисунок Д3.24
Таблиця Д3.24
Задача Д3.25
На горизонтальну платформу D1 помістили тіло Р масою m, яке приєднали до системи пружин жорсткостями с1 і с2, причому на пру-жини жорсткістю с1 діє в горизонтальному напрямку повзун В, що показано на рис. Д3.25. В деякий моментчасу тілу Р надають початкову швидкість V0, а повзун В починає виконувати рух за законом
x = H1 sin(p1t) + H2 sin(p2t).
Визначити рівняння руху тіла Р і побудувати графік залежності координати від часу, якщо тіла D 1 і D2 вважаються невагомими, рухаються поступально, а тертя відсутнє.
Дані для остаточних розрахунків містяться в таблиці Д3.25 по варі-антах.
Рисунок Д3.25
Таблиця Д3.25
Задача Д3.26
Тіло Р масою m приєднано до горизонтальних пружин жорст-костями с1, с2, с3 і демпфера D за допомогою невагомого стержня В, як показано на рис. Д3.26. При русі тіла Р демпфер створює силу опору R, яка має напрямок протилежний до швидкості V і опису-ється залежністю R = m V, де m - коефіцієнт в’язкості рідини, яка міститься в демпфері. В початковий момент часу тілу Р надають початкову швидкість V0 і зміщення xo, після чого воно виконує рух вздовж горизонтальної осі x.
Визначити рівняння руху тіла Р і побудувати графік залежності координати від часу, якщо стержень В рухається поступально, від-хилення від положення рівноваги малі і горизонтальні.
Дані для остаточних розрахунків - в таблиці Д3.26 по варіантах.
Рисунок Д3.26
Таблиця Д3.26
Задача Д3.27
Тіло Р масою m ковзає по похилій гладенькій площині з кутом a до горизонту після чого падає на невагому платформу В, яка опирає-ться на пружини жорсткостями с1, с2, с3 і демпфер D, як показано на рис. Д3.27. На початку руху тілу Р надають початкову швидкість U в напрямку площини і воно до дотику з платформою В проходить шлях l. При русі тіла Р разом з платформою демпфер D створює силу опору R, яка має напрямок проти лежний до швидкості V і описується залежністю R = m V, де m - коефіцієнт в’язкості рідини, яка міститься в демпфері.
Визначити рівняння руху тіла Р і побудувати графік залежності координати від часу, якщо платформа В рухається поступально, а удар тіла Р до платформи В абсолютно непружний.
Дані для остаточних розрахунків в таблиці Д3.27 по варіантах.
Рисунок Д3.27
Таблиця Д3.27
Задача Д3.28
На похилій площині з кутом 30o до горизонту розташований ван-
таж Р мaсою m, який закріплено до нижнього кінця системи пру-жин с1, с2 і с3, а до верхнього кінця пружин прикріплено повзун В, що показано на рис. Д3.28. Система знаходиться в положенні статичної рівноваги. В деякий момент часу повзун В починає вздовж похилої площини рух за законом
x =H1 sin(p1t) + H2 cos(p2t).
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо тертя відсутнє, а масою пластини D, яка рухаєься поступально, нехтуємо.
Дані для остаточних розрахунків містяться в таблиці Д3.28 по варі-антах.
Рисунок Д3.28
Таблиця Д3.28
Задача Д3.29
На похилій площині з кутом a до горизонту розташований ван-
таж Р мaсою m, який закріплено до верхнього кінця системи пру-жин с1, с2 , с3 і до демпфера D, що показано на рис. Д3.29. Система знаходиться в положенні статичної рівноваги. При русі тіла демпфер D створює силу опору залежну від швидкості: R = m V. В початковий момент часу тілу Р надають початкове зміщення xo і початкову швидкість Vo, після чого воно рухається вздовж осі х.
Визначити рівняння руху вантажу Р і побудувати графік залеж-ності координати від часу, якщо тертя відсутнє, а масою тіла В, яке рухається поступально, нехтуємо.
Дані для остаточних розрахунків містяться в таблиці Д3.29 по варіантах.
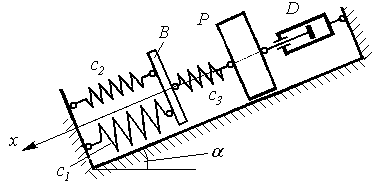
Рисунок Д3.29
Таблиця Д3.29
Задача Д3.30
Два вантажі Р1 і Р2 масами m1 і m2, відповідно, знаходяться на невагомій платформі В, яка підтримується системою пружин жорс-ткостями с1, с2, с3 і c4 як показано на рис. Д3.30. Маси вантажів Р1 і Р2 складають відношення: m1/m2 = n, а при вільних коливаннях вказаних вантажів циклічна частота рівна k. В положенні статичної рівноваги платформа В зміщена на lст .
В початковий момент часу вантаж Р2 знімають, при цьому вантаж Р1 набуває початкову швидкість Vo в вертикальному напрямку. Знайти рівняння коливного руху вантажу Р 1, побудувати графік залежності координати від часу, визначити амплітуду (А), період (Т) та початкову фазу (j o), якщо платформа В рухається поступально, а опором середовища нехтуємо.
Дані для остаточних розрахунків містяться в таблиці Д3.30 по варіантах.
Рисунок Д3.30
Таблиця Д3.30
