Однорідне тіло 1 обертається навколо горизонтальної осі під дією моменту М (рис. 4.7) і до нього прикладені зовнішні сили: сила тяжіння P1=m1g; реакції циліндричного шарніра Х1 та Y1, зусилля у ланках паса S5 та S4.
Рисунок 4.7
Запишемо диференціальне рівняння обертання тіла 1 навколо нерухомої осі Z.
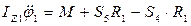. (4.1)
Необхідно врахувати, що момент сили або пари сил буде додатним, якщо він діє у напрямку руху тіла. Так, у рівнянні (4.1) момент сили S5 та пари сил з моментом М беремо із додатним знаком, а момент сили S4 – з від’ємним.
Момент інерції тіла 1 відносно осі Z
(4.2)
На тіло 2 (рис 4.8) під час руху діють зовнішні сили: сила тяжіння P2=m2g, реакції нерухомого шарніра Х2 та Y2, зусилля у ланках паса 
та S4`, реакції тіла 1 – S2 та N2.
У диференціальному рівнянні руху тіла 2 (рис. 4.8) навколо горизонтальної осі Z
(4.3)
сили = 
та 
, а момент інерції тіла 2 відносно осі Z знайдемо через радіус інерції і2
(4.4)
Рисунок 4.8
Для тіла 3 (рис. 4.9), що переміщується під дією сили тяжіння Р3=m3g, реакції нерухомих шарнірів NA та NB, реакції 
та 
тіла 2, запишемо теорему про рух центра мас в проекціях на вісь Y (вісь Y направляється в сторону руху тіла 3)
(4.5)
Звичайно 
Якщо диференціальні рівняння (4.1), (4.3) і (4.5) розглянути з кінематичними співвідношеннями
, 
. (4.6)
Тоді отримаємо п’ять рівнянь з невідомими 
Рисунок 4.9
Розв’язуючи систему рівнянь (4.1), (4.3), (4,5), (4,6), і, враховуючи (4.2) та (4.4), маємо
Або, підставляючи дані умови задачі, отримаємо
При t1=2c, 
Визначення реакцій в’язей циліндричних шарнірів та зусиль між тілами
Для тіл 1 та 2 запишемо теорему про рух центра мас в проекціях на осі х та у.
Тіло 1 (рис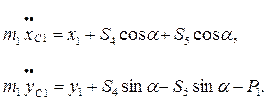. 4.7)
(4.7)
Тіло 2 (рис 4.8)
(4.8)
Для тіла 3 (рис. 4.9) в проекціях на вісь Х:
(4.9)
В рівняннях (4.7) – (4.9) 
оскільки центри мас тіл 1, 2 знаходяться на нерухомих осях обертання тіл, а координати XC3 тіла 3 є сталою величиною.
Отримали систему п’яти рівнянь
(4.8)
в якій сім невідомих величин: x1, y1, x2, y2, N2, NB, NA.
Додаткові два рівняння отримаємо, використовуючи закон Амонтока-Кулона
(4.9)
та диференціальне рівняння обертального руху тіла 3 навколо осі Z що проходить через центр мас С (рис. 4.9) тіла 3
(4.10)
Тіло 3 рухається поступально і тому 
Таким чином, із (4.10) маємо
(4.11)
Розв’язуючи систему рівнянь (4.6), (4.9) і (4.11), отримаємо
ДС. 5 Визначення прискорення точок та кутових прискорень тіл за допомогою теореми про зміну кінетичної енергії системи
Матеріальна система (рис. 4.1-4.5) приводиться до руху моментом М. Знайти прискорення тіла 3 та кутові прискорення тіл в момент часу t=t1.
Масами пасів та їх ковзанням по шківах знехтувати. В точках контакту тіл ковзання відсутнє. Однорідний диск 1 та ступінчатий шків 2 обертаються навколо горизонтальних осей.
Дані для розрахунку приведені в таблиці 4.1 де m1, m2, m3 – маси тіл 1, 2 та 3; R1, R2, r2 – розміри тіл 1 та 2; і2 – радіус і перції тіла 2 відносно горизонтальної осі.
