Тонкий стержень вагою Р (рис. 3.1-3.5) жорстко скріплений з круговим диском (парні варіанти) або тонким кільцем (непарні варіанти) вагою Q та радіусом r. Система обертається навколо горизонтальної осі в вертикальній площині із стану спокою під дією моменту М. Знайти кутове прискорення, кутову швидкість та зусилля в опорах осі при повороті системи на кут 
.
Стержень, диск, кільце вважати однорідними тілами; тертям в підшипниках знехтувати. Дані для розрахунку приведені в таблиці 3.1.
Таблиця 3.1.
| Варіант | Р, Н | Q, H | r, м | АВ, м | М, Н м | , град
|
| 0,1 0,3 0,4 0,1 0,2 0,3 0,4 0,1 0,2 0,3 | 0,3 0,9 1,0 0,4 0,6 1,0 1,2 0,3 0,5 0,8 |
Приклад виконання завдання
Система тіл, що складається з стержня 1 вагою Р, однорідного диска 2 та кільця 3, що мають відповідно вагу Q2 та Q3 та радіус R, обертається навколо горизонтальної осі О (рис. 3.6.) під дією пари сил з моментом М. Знайти кутове прискорення, кутову швидкість та зусилля в опорах осі при повороті матеріальної системи на кут , якщо в початковий момент часу система знаходилася в спокої.
Прийняти: P=10H; Q2=20H; M=30Hм; Q3=10H; R=0,2м; AO=0,8м; =600. 
Рисунок 3.1
Рисунок 3.2
Рисунок 3.3
Рисунок 3.4
Рисунок 3.5
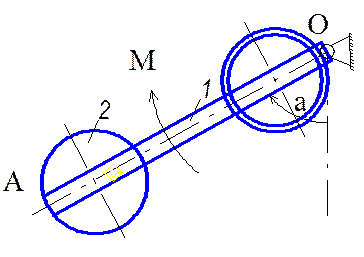
Рисунок 3.6
Розв’язання. На систему тіл діють активні сили 
, 
, 
та пара сил з моментом М (рис.3.7)
Переміщенню тіл перешкоджає в’язь: циліндричний шарнір О, дію якого на тіло, на підставі аксіоми звільнення від в’язів, замінюємо реакціями в’язей 
0, 
0.
Для визначення сил 0, 0 запишемо теорему про рух центра мас системи в проекціях на осі Х та Y.
М 
с=Fxе, (3.1)
М 
с=Fyе,
де М=m1+m2+m3- маса системи тіл (m1= 
, m2= 
, m3= 
), с і с-проекція прискорення центра мас системи на осі Х та Y, Fxе і Fyе- проекція головного вектора зовнішніх сил системи на осі Х та Y.
Fxе =Х0,
Fyе=Y0-P-Q2-Q3. (3.2)
Тепер із диференціальних рівнянь (3.1) отримаємо
Х0=М 
с,
Y0=M 
+P (3.3)
Щоб знайти реакції в’язей необхідно визначити прискорення центра мас 
системи тіл
(3.4)
де 
, 
, 
-кутова швидкість тіла,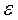 
- кутове прискорення тіла (системи тіл.)
Визначення кутового прискорення системи тіл
Кутове прискорення тіл знайдемо на підставі диференціального рівняння обертального руху тіла навколо осі 
.
. (3.5)
де Iz – момент інерції системи тіл відносно осі Z,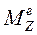 
- головний момент зовнішніх сил системи відносно осі Z.
Момент інерції тіл IZ відносно осі дорівнює сумі моментів інерції тіл 1, 2, 3 відносно осі Z.
= 
+ 
+ 
Момент інерції диска 2 відносно осі Z:
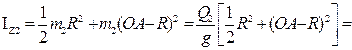
Момент інерції кільця 3 відносно осі Z:
.
Момент інерції стержня 1 відносно осі Z:
.
Тоді: 
.
Момент зовнішніх сил матеріальної системи (рис.3.7) відносно осі Z
. (3.6)
де OC 
, OC 
і OC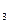 
відстань осі обертання до центра мас відповідного тіла.
Момент сили або момент пари сил беремо з додатним знаком, якщо він діє у напрямку обертання системи тіл.
Диференціальне рівняння (3.5), враховуючи (3.6), запишеться:
.
Звідки:
= 
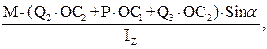
(3.7)
При =600, 
