Матеріальна система (рис. 13.1) починає рухатись із стану спокою під дією моменту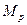 
електродвигуна 5. Через 
секунд ротор електродвигуна раптово зупинився. Знайти закон руху тіла 1. Осі тіл 1, 5 та 2 лежать в горизонтальній площині.
Таблиця 13.1
| В-т |  ,
| 
|  ,
|  ,
|  ,
|  ,
|  ,
|  ,
|  ,
|  ,
| ,
|
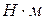
| 0,005 | 0,3 | 0,2 | 0,25 | 0,1 | 100+9(7-t) | 1,2 | |||||
| 0,01 | 0,4 | 0,25 | 0,3 | 0,15 | 150+11(7-t) | 1,4 | |||||
| 0,015 | 0,5 | 0,3 | 0,4 | 0,2 | 150+13(7-t) | 1,6 | |||||
| 0,02 | 0,6 | 0,4 | 0,5 | 0,1 | 500+20(7-t) | 1,8 | |||||
| 0,015 | 0,55 | 0,35 | 0,4 | 0,16 | 600+62(7-t) | 2,0 | |||||
| 0,01 | 0,5 | 0,3 | 0,4 | 0,2 | 550+5(7-t) | 2,2 | |||||
| 0,05 | 0,45 | 0,2 | 0,3 | 0,15 | 300+27(7-t) | 2,4 | |||||
| 0,01 | 0,35 | 0,15 | 0,2 | 0,2 | 200+15(7-t) | 2,6 | |||||
| 0,004 | 0,3 | 0,1 | 0,2 | 0,1 | 150+10(7-t) | 2,8 | |||||
| 0,08 | 0,4 | 0,2 | 0,3 | 0,2 | 250+20(7-t) | 3,0 |
При розрахунку прийняти: 
, 
, 
.
Рисунок 13.1
Розв’язання. Якщо за узагальнену координату прийняти кут повороту 
(рис. 13.2) тіла 1 від положення статичної рівноваги, тоді рівняння Лагранжа II роду запишеться:
, (13.1)
де 
– кінетична енергія системи;
– узагальнена сила узагальненої координати ;
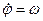– узагальнена швидкість;
– узагальнена координата з початком в положенні статичної рівноваги системи (
).
Знайдемо кінетичну енергію системи, яка складається з суми кінетичних енергій тіл 1, 2, 3 і 5:
(13.2)
Рисунок 13.2
Тіла 1, 2 та 5 обертаються навколо нерухомих горизонтальних осей і їх кінетична енергія знаходиться за формулами:
, (13.3)
де 
, 
– моменти інерції відповідно тіл 1 та 2;
Тіло 3 переміщується поступально із швидкістю 
, тоді:
, (13.4)
де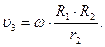 
Кінетична енергія системи (13.2), враховуючи (13.3) та (13.4), запишеться:
, (13.5)
де 
– зведений момент інерції системи.
Знайдемо величини, що входять в ліву частину рівняння Лагранжа II роду (13.1).
(13.6)
Узагальнену силу визначимо за формулою:
, (13.7)
де 
– віртуальна робота активних сил;
– варіація узагальненої координати (бажано надавати в сторону збільшення координати ).
Визначимо віртуальну роботу активних сил системи (рис.13.2) враховуючи, що при зупинці ротора електродвигуна 
(13.8)
де 
– статична деформація пружної муфти, 
Або:
(13.9)
Узагальнена сила (13.7), враховуючи (13.9), запишеться:
(13.10)
Оскільки матеріальна система консервативна, тоді узагальнену силу можемо знайти іншим методом за формулою:
.
Потенціальна енергія системи П визначається роботою моменту пружної муфти та сили ваги тіла 3 на переміщенні системи із зміщеного положення, коли тіло 1 має координату φ, в нульове положення статичної рівноваги:
П=П(мпр)+П(Р3),
де П(мпр)=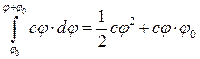 
,
П(Р3)= 
Тоді 
.
В положенні статичної рівноваги:
тоді 
.
І узагальнена сила знаходиться за формулою:
Таким чином, рівняння Лагранжа II роду (13.1) набуває вигляду:
(13.11)
Або
де 
Циклічна частота вільних коливань
.
Інтегруючи диференціальні рівняння (13.11), отримуємо рівняння руху тіла 1:
(13.12)
Для визначення постійних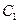 
та 
знайдемо кутову швидкість тіла 1:
(13.13)
Використаємо початкові умови задачі при
, 
, 
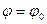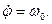(13.14)
Тоді із рівнянь (13.12) і (13.13) маємо:
, 
. (13.15)
Початкову кутову швидкість 
знайдемо на підставі теореми про зміну кінетичної енергії системи:
(13.16)
де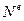 
– потужність зовнішніх сил (рис. 13.3);
– потужність внутрішніх сил.
Нехтуючи потужністю моменту пружної муфти, приймаємо Nі=0.
Рисунок 13.3
Потужність зовнішніх сил:
, (13.17)
де 
;
Із теореми (13.16), враховуючи (13.5) та (13.17), знаходимо:
.
.
Або: 
. (13.18)
Інтегруємо рівняння (13.18) при умовах, що:
при ; 
,
при 
; 
.
Отримуємо: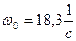 
.
Для визначення 
, розглянемо рух ротора електродвигуна (рис.13.4)
Рисунок 13.4
Запишемо диференціальне рівняння руху ротора навколо нерухомої осі 
:
, (13.19)
де 
– момент, який передає пружна муфта.
Із (13.19) та (13.18) при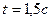 
знаходимо:
,
.
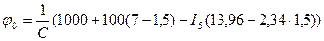Тепер рівняння руху тіла 1 (13.12), враховуючи (13.15), запишеться:
,
Амплітуда коливань 
:
, 
.
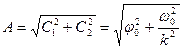Період коливань 
:
, 
.
Відповідь: φ=0,0077 сos68.4t+0.2675sin68.4t.
Література
1. Бать Н. М., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах: В 3 т. – Т.2 – М.: Наука, 1985. – 560с.
2. Березова О. В., Друшляк Г. Е., Солодовников Р. В. Теоретическая механика: Сб. задач. – К.: Высш. шк. Главное изд – во, 1980. – 324 с.
3. Бражниченко Н. А. и др. Сборник задач по теоретической механике / Н. А. Бражниченко, Н. Л. Кац, Б. Л. Минцберг, В. Н. Морозов. – М.: Судпромгиз, 1963. – 562 с.
4. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики: В 2 т. – Т.2. – М.: Наука, 1979. – 461 с.
5. Бухгольц Н. Н. Основной курс теоретической механики: В 2 ч. – М.: Наука, 1967. – ч. 1. – 468 с.; ч. 2. – 332 с.
6. Добронравов В. В., Никитин Н. Н., Дворников А. Л. Курс теоретической механики, – М.: Высш. шк., 1974. – 528 с.
7. Кильчевский Н. А. Курс теоретической механики: В 2 т. – М.: Наука, 1972 – 1977. – Т.1. – 456 с.; Т.2. – 462 с.
8. Ключев В. И., Терехов І. Б. Электропривод и автоматизация общепромышленных механизмов: Учебник для вузов, - М.: Энергия, 1980. – 360 с.
9. Лойцянский Л. Г., Лурье А. И. Курс теоретической механики: В 2 т. – М.: Наука, 1984. – Т.1. – 352 с.; Т.2. – 640 с.
10. Павловський М. А. Теоретична механіка: Підручник. – К.: Техніка, 2002. – 512 с.
11. Приятельчук В. О., Риндюк В. І., Федотов В. О. Теоретична механіка. Динаміка матеріальної системи. Розрахунково-графічні та контрольні завдання. Навчальний посібник – Вінниця: ВНТУ, 2005. – 85 с.
12. Савин Г. Н., Путяга Т. В., Фрадлин Б. Н. Курс теоретической механики. –К.: Высш. шк., 1973. – 359 с.
13. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособ. для техн. вузов / Яблонский А. А., Норейко С. С., Вольфсон С. А. и др.; Под ред. А. А.Яблонского. – 4-е изд. перераб. и доп. – М.: Высш. шк., 1985. – 367 с.
14. Сендлер А. С. Электропривод и автоматизация металлорежущих станков: Учебное пособие. – М.: ВШ, 1972. – 440 с.
15. Яблонский А. А., Никифорова В. М. Курс теоретической механики: В 2 т. – М.: Высш. шк., 1977. – Т.1. – 431 с.; Т.2.– 532 с.
16. Яскілка М. Б. Збірник завдань для розрахунково-графічних робіт з теоретичної механіки: Посібник. – К.: Вища шк.: Веселка, 1999. – 351с.
Навчальне видання
Андрій Андрійович Видмиш
Володимир Олексійович Приятельчук
Валерій Олександрович Федотов
ТЕОРЕТИЧНА МЕХАНІКА
ДИНАМІКА
