| 16.1.2
По заданному уравнению вращения φ = 2(t 2 + 1) материального тела с осевым моментом инерции относительно оси вращения Iz = 0,05 кг·м2 определить главный момент внешних сил, действующих на тело. (0,2)
|
| 16.1.3
Диск вращается вокруг оси Oz по закону φ = t 3. Определить модуль момента пары сил, приложенных к диску, в момент времени t = 1 с, если момент инерции диска относительно оси вращения Iz = 2 кг·м2.
(12)
|
| 16.1.4
По заданному уравнению вращения φ = 3 t 2 – t стержня с осевым моментом инерции Iz = 1/6 кг·м2 определить главный момент внешних сил, действующих на стержень. (1)
|
 16.1.10
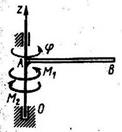
Однородный стержень, масса которого m = 2 кг и длина АВ = 1 м, вращается вокруг оси Oz под действием пары сил с моментом М1 и момента сил сопротивления М2 = 12 Н·м по закону φ = 3 t 2. Определить модуль момента М1 приложенной пары сил в момент времени t = 1 с.
(16) 16.1.10
Однородный стержень, масса которого m = 2 кг и длина АВ = 1 м, вращается вокруг оси Oz под действием пары сил с моментом М1 и момента сил сопротивления М2 = 12 Н·м по закону φ = 3 t 2. Определить модуль момента М1 приложенной пары сил в момент времени t = 1 с.
(16)
|
16.1.11
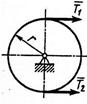 Определить угловое ускорение диска массой m = 50 кг, радиуса r = 0,3 м, если натяжение ведущей и ведомой ветвей ремня соответственно равны Т 1 = 2 Т 2 = 100 Н. Радиус инерции диска относительно оси вращения iz = 0,2 м.
(7,5) Определить угловое ускорение диска массой m = 50 кг, радиуса r = 0,3 м, если натяжение ведущей и ведомой ветвей ремня соответственно равны Т 1 = 2 Т 2 = 100 Н. Радиус инерции диска относительно оси вращения iz = 0,2 м.
(7,5)
|
 16.1.13
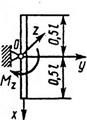
Определить угловое ускорение однородного стержня массой m = 4 кг и длиной l = 1 м, вращающегося вокруг оси Oz, если к стержню приложен вращающий момент Mz = 3 Н·м.
(9) 16.1.13
Определить угловое ускорение однородного стержня массой m = 4 кг и длиной l = 1 м, вращающегося вокруг оси Oz, если к стержню приложен вращающий момент Mz = 3 Н·м.
(9)
|
 16.1.14
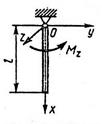
Определить угловое ускорение вращения вокруг оси Oz однородного стержня массой m = 3 кг и длиной l = 1 м. На стержень действует пара сил с моментом Mz = 2 Н·м.
(2) 16.1.14
Определить угловое ускорение вращения вокруг оси Oz однородного стержня массой m = 3 кг и длиной l = 1 м. На стержень действует пара сил с моментом Mz = 2 Н·м.
(2)
|
| 16.1.22
Маховик массой m = 5 кг вращается вокруг оси Oz по закону φ = 9 t 2 + 2. Определить радиус инерции iz маховика, если его вращение вызвано действием вращающего момента Mz = 180 Н·м.
(1,41)
|
16.1.23
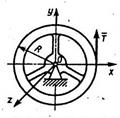 Определить радиус инерции iz шкива, масса которого m = 50 кг и радиус r = 0,5 м, если под действием силы натяжения троса Т = 18 t Н он вращается вокруг оси Oz по закону φ = t 3/3 + 3 t.
(0,3) Определить радиус инерции iz шкива, масса которого m = 50 кг и радиус r = 0,5 м, если под действием силы натяжения троса Т = 18 t Н он вращается вокруг оси Oz по закону φ = t 3/3 + 3 t.
(0,3)
|
| 16.1.24
Маховик массой m = 3 кг под действием вращающего момента Mz = 9 t Н·м вращается вокруг оси Oz по закону φ =2t 3. Определить радиус инерции iz маховика.
(0,5)
|
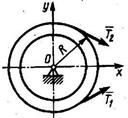 16.1.25
Определить радиус инерции шкива массой m = 5 кг и радиуса r = 0,4 м, если под действием сил натяжения ремня Т1 = 2 Т2 = 10 Н он вращается с угловой скоростью ω = 10 t.
(0,2) 16.1.25
Определить радиус инерции шкива массой m = 5 кг и радиуса r = 0,4 м, если под действием сил натяжения ремня Т1 = 2 Т2 = 10 Н он вращается с угловой скоростью ω = 10 t.
(0,2)
|
 Натяжение ведущей и ведомой ветвей ремня, приводящего во вращение шкив радиуса r = 20 см и массы m = 3,27 кг, соответственно равны: Т1 = 100 Н, Т2 = 50 Н. Чему должен быть равен момент сил сопротивления для того, чтобы шкив вращался с угловым ускорением ε = 1,5 рад/с2? Шкив считать однородным диском. (9,8)
Натяжение ведущей и ведомой ветвей ремня, приводящего во вращение шкив радиуса r = 20 см и массы m = 3,27 кг, соответственно равны: Т1 = 100 Н, Т2 = 50 Н. Чему должен быть равен момент сил сопротивления для того, чтобы шкив вращался с угловым ускорением ε = 1,5 рад/с2? Шкив считать однородным диском. (9,8)
|
| Маховик в момент включения тормоза имеет угловую скорость ω = 4 рад/с. Тормозящий момент постоянный и равен Мтр= 10 Н·м. Момент инерции маховика относительно оси вращения равен Iz = 20 кг·м2. Определить время до остановки маховика. (8)
|
| Маховик в момент включения тормоза имеет угловую скорость ω = 5 рад/с. Тормозящий момент постоянный и равен Мтр= 15 Н·м. Момент инерции маховика относительно оси вращения равен Iz = 30 кг·м2. Определить время до остановки маховика. (10)
|
| Маховик в момент включения тормоза имеет угловую скорость ω = 6 рад/с. Тормозящий момент постоянный и равен Мтр= 10 Н·м. Момент инерции маховика относительно оси вращения равен Iz = 35 кг·м2. Определить время до остановки маховика. (21)
|
 16.1.10
Однородный стержень, масса которого m = 2 кг и длина АВ = 1 м, вращается вокруг оси Oz под действием пары сил с моментом М1 и момента сил сопротивления М2 = 12 Н·м по закону φ = 3 t 2. Определить модуль момента М1 приложенной пары сил в момент времени t = 1 с.
(16)
16.1.10
Однородный стержень, масса которого m = 2 кг и длина АВ = 1 м, вращается вокруг оси Oz под действием пары сил с моментом М1 и момента сил сопротивления М2 = 12 Н·м по закону φ = 3 t 2. Определить модуль момента М1 приложенной пары сил в момент времени t = 1 с.
(16)
 Определить угловое ускорение диска массой m = 50 кг, радиуса r = 0,3 м, если натяжение ведущей и ведомой ветвей ремня соответственно равны Т 1 = 2 Т 2 = 100 Н. Радиус инерции диска относительно оси вращения iz = 0,2 м.
(7,5)
Определить угловое ускорение диска массой m = 50 кг, радиуса r = 0,3 м, если натяжение ведущей и ведомой ветвей ремня соответственно равны Т 1 = 2 Т 2 = 100 Н. Радиус инерции диска относительно оси вращения iz = 0,2 м.
(7,5)
 16.1.13
Определить угловое ускорение однородного стержня массой m = 4 кг и длиной l = 1 м, вращающегося вокруг оси Oz, если к стержню приложен вращающий момент Mz = 3 Н·м.
(9)
16.1.13
Определить угловое ускорение однородного стержня массой m = 4 кг и длиной l = 1 м, вращающегося вокруг оси Oz, если к стержню приложен вращающий момент Mz = 3 Н·м.
(9)
 16.1.14
Определить угловое ускорение вращения вокруг оси Oz однородного стержня массой m = 3 кг и длиной l = 1 м. На стержень действует пара сил с моментом Mz = 2 Н·м.
(2)
16.1.14
Определить угловое ускорение вращения вокруг оси Oz однородного стержня массой m = 3 кг и длиной l = 1 м. На стержень действует пара сил с моментом Mz = 2 Н·м.
(2)
 Определить радиус инерции iz шкива, масса которого m = 50 кг и радиус r = 0,5 м, если под действием силы натяжения троса Т = 18 t Н он вращается вокруг оси Oz по закону φ = t 3/3 + 3 t.
(0,3)
Определить радиус инерции iz шкива, масса которого m = 50 кг и радиус r = 0,5 м, если под действием силы натяжения троса Т = 18 t Н он вращается вокруг оси Oz по закону φ = t 3/3 + 3 t.
(0,3)
 16.1.25
Определить радиус инерции шкива массой m = 5 кг и радиуса r = 0,4 м, если под действием сил натяжения ремня Т1 = 2 Т2 = 10 Н он вращается с угловой скоростью ω = 10 t.
(0,2)
16.1.25
Определить радиус инерции шкива массой m = 5 кг и радиуса r = 0,4 м, если под действием сил натяжения ремня Т1 = 2 Т2 = 10 Н он вращается с угловой скоростью ω = 10 t.
(0,2)
 Натяжение ведущей и ведомой ветвей ремня, приводящего во вращение шкив радиуса r = 20 см и массы m = 3,27 кг, соответственно равны: Т1 = 100 Н, Т2 = 50 Н. Чему должен быть равен момент сил сопротивления для того, чтобы шкив вращался с угловым ускорением ε = 1,5 рад/с2? Шкив считать однородным диском. (9,8)
Натяжение ведущей и ведомой ветвей ремня, приводящего во вращение шкив радиуса r = 20 см и массы m = 3,27 кг, соответственно равны: Т1 = 100 Н, Т2 = 50 Н. Чему должен быть равен момент сил сопротивления для того, чтобы шкив вращался с угловым ускорением ε = 1,5 рад/с2? Шкив считать однородным диском. (9,8)




