Задачи для самостоятельного решения. Инерция –явление сохранения телом при отсутствии внешних воздействий состояния покоя или равномерного прямолинейного движения

ДИНАМИКА

Основные понятия

 

Инерция – явление сохранения телом при отсутствии внешних воздействий состояния покоя или равномерного прямолинейного движения.

Масса тела – физическая скалярная величина, характеризующая инертность тела, т.е. масса – количественная мера инертности тела.

Закон сохранения массы: M = m₁ + m₂ + … + m_n

Сила – физическая векторная величина, характеризующая результат взаимодействия тел и являющаяся причиной изменения механического состояния тела или (и) его деформации, т.е. сила – количественная мера взаимодействия тел, в результате которого изменятся механическое состояние тела или (и) происходит его деформация.

Следует иметь ввиду, что воздействие одного тела на другое может происходить как при непосредственном контакте, так и посредством силовых полей: гравитационное, электрическое и магнитное поля.

Равнодействующая всех сил, приложенных к телу.

Если к материальной точке (частице) приложено несколько сил, то их действие можно заменить действием одной силы R, которая является равнодействующей данных сил (принцип суперпозиции сил): R = F₁ + F₂ + F₃ + … + F_n

Замечание. Если реально действующие силы заменены равнодействующей, то в дальнейшем следует считать, что к частице приложено не несколько сил, а только одна - их равнодействующая.

Основой динамики и всей классической механики служат три закона Ньютона, сформулированные для материальной точки и тел, движущихся поступательно в инерциальных системах отсчета.

I – ый закон Ньютона

Существуют такие системы отсчета, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока на него не подействует какое-либо другое тела (тела), т.е. если равнодействующая всех сил, приложенных к телу (материальной точке), равна нулю, то оно сохраняет состояние покоя или равномерного прямолинейного движения: F = å F = 0; V = const.

Из первого закона динамики следует, что свободное движение частиц с постоянной скоростью - движение по инерции есть такое же естественное состояние частиц, как и покой. Каждая частица мoжeт двигаться с какой угодно постоянной скоростью без каких бы то ни было внешних воздействий со стороны, но изменить свое движение - сообщить себе ускорение не может. Состояния покоя и равномерного прямолинейного движения с точки зрения динамики неразличимы.

II – ый закон Ньютона

Ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, и обратно пропорционально его массе и совпадает по направлению с направлением действующей силы. a = SF /m

Это уравнение является основным уравнением динамики материальной точки.

Замечание.

При его использовании нужно иметь в виду следующее.

1. Действие сил на материальную точку не зависит друг от друга, т.е. каждая из сил, F₁, F₂,..., F_n, приложенных к частице, coо6щает ей такое ускорение, как если бы других сил нс было (принцип независимости действия сил).

2. Результирующее ускорение частицы a, находящейся под действием нескольких сил, равно геометрической сумме ускорений a₁, a₂,..., a_n сообщаемых каждой силой в отдельности. Модуль и направление ускорения a таковы, как если бы на частицу действовала одна сила, равная векторной сумме приложенных сил, т. е. основное уравнение динамики точки справедливо как для отдельных сил, так и для их равнодействующей.

3.. Если равнодействующая сила R и скорость V направлены по одной прямой (под действием сил изменяется только модуль скорости), то движение материальной точки будет прямолинейным и ускоренным.

Если же при этом на материальную точку действуют силы, равнодействующая которых с течением времени не меняется (R = const), то движение точки будет прямолинейным и равноускоренным (а = const).

В частном случае, когда R = 0, то a = 0 и, следовательно, V = const, т.е. движение точки будет прямолинейным и равномерным.

4. Если же равнодействующая направлена под углом к вектору скорости, то движение материальной точки будет криволинейным.

В общем случае такого движения под действием сил изменяются и модуль, и направление скорости.

Если же в течение всего времени движения равнодействующая перпендикулярна скорости и с течением времени не меняется по модулю (R = const, R ^V), то модуль вектора скорости остается постоянным (V = const), а ее направление за любые равные промежутки времени меняется на одинаковый угол, т.е. в этом случае точка равномерно движется по окружности.

Материальная точка может описывать окружность (или дугу окружности) и в том случае, если равнодействующая приложенных сил образует с вектором скорости острый или тупой угол. Для этого необходимо, чтобы составляющие равнодействующей R по направлению вектора скорости и направлению, ему перпендикулярному, вызывающие соответственно касательное и нормальное ускорение точки, изменялись так, чтобы в каждый момент времени имело место равенство: R_n = mV²/r при постоянном r, где r - радиус вращения точки.

III – ый закон Ньютона

Всякому действию всегда есть равное и противоположно направленное противодействие, т.е. два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению; приложены эти силы к разным телам. F₁₂ = - F₂₁

Замечание.

Равенство модулей сил при взаимодействии имеет место всегда, независимо от того, находятся ли взаимодействующие тела в относительном покое или они движутся, контактируют непосредственно или посредством силовых полей.

Виды сил.

Сила тяготения – сила взаимодействия между двумя телами, обладающими массами.

Две материальные точки (два однородных шара) притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними (между их центрами) (закон всемирного тяготения):

F = G m₁ m₂/R², где G = 6,67 10 Нм² /кг² – гравитационная постоянная.

Замечание.

Массы, входящие в этот закон являются мерой гравитационного взаимодействия тел. Опыт показывает, что гравитационная и инертная массы равны.

 

Если тело массы m находится на поверхности планеты массой M, то сила притяжения этого тела к планете составляет:

F = G m M / R², где R – радиус планеты.

Если тело массы m находится над поверхностью планеты массой M на высоте h от его поверхности, то сила притяжения этого тела к планете составляет:

F = G m M / (R+h)², где R – радиус планеты.

Предоставленное действию одной этой силы, всякое тело падает ускоренно по направлению отвесной линии и одновременно с этим участвует в суточном вращении земного шара, обладая центростремительным ускорением. Эти ускорения создаются составляющими силы притяжения по направлению отвесной линии и радиуса окружности, описываемой телом вокруг земной оси.

Составляющую силы земного притяжения по отвесному направлению в данной точке земного шара, равную mg, называют силой тяжести, а ускорение g, создаваемое этой силой, - ускорением свободного падения.

В связи с малостью угловой скорости вращения Земли (w = 0, 00727 с^-1) сила тяжести практически совпадает с силой тяготения и при h << R_Земли ускорение силы тяжести g можно рассчитать следующим образом:

g = G M_З / R_з ², где M_З - масса Земли, R_з - радиус Земли.

Очевидно, что, если не учитывать вращение Земли и считать ее шаром, то на расстояниях h << R_Земли ускорение свободного падения не зависит от массы тела

Следовательно, сила тяжести – это сила, с которой тело притягивается в данной точке к Земле. Она приложена к телу. F_{тяжести} = m g

Вес тела – сила, с которой тело вследствие его притяжения к Земле действует на горизонтальную опору или растягивает вертикальную нить подвеса.

Вес тела приложен к опоре или к нити подвеса.

Следует иметь в виду, что по модулю вес и сила тяжести могут сильно отличаться друг от друга, т.к. вес тела зависит от характера движения подставки (подвеса). Так, например, при невесомости вес тела равен нулю, а при перегрузке модуль веса может превышать во много раз модуль силы тяжести, в то время как в случае покоя подставки (подвеса) их модули равны, поэтому отождествление их может привести к абсурду.

Вес тела называют статическим P₀, если подставка или нить подвеса неподвижны относительно выбранной системы отсчета, и динамическим P, если подставка или нить подвеса подвижны.

Следует иметь в виду, что статический вес для данного тела постоянен: P₀ = m g, а динамический – не постоянен и зависит от величины и направления ускорения, а также от направления движения подставки (подвеса): P = m (g - a).(см. рисунок 1a) или P = m (g + a).(см. рисунок 1b).

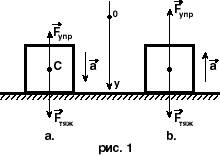
В общем случае можно записать, что P = nP₀, где n – коэффициент перегрузки.

При n = 0 наступает состояние невесомости, при n > 1 - перегрузка.

Сила упругости – сила, возникающая при деформации тел и препятствующая изменению объема и формы тела.

В пределах упругости справедлив закон Гука: F = - k Dx, где k – коэффициент упругости (жесткость), Dx – величина деформации.

 

Замечание. Упругими деформациями называются такие деформации, после снятия которых тело полностью восстанавливает свои первоначальные форму и объем.

 

Введем некоторые понятия.

Механическим напряжением s называется отношение величины приложенной к образцу нагрузки к площади его поперечного сечения: s = F/ S

Относительным удлинением образца называется отношение: e = Dl / l₀, где Dl - абсолютное удлинение образца, l - конечная длина образца, l₀ - начальная длина образца.

Тогда s = e Е, где Е – модуль Юнга (вторая формулировка закона Гука: в пределах упругости напряжение, возникающее в образце, пропорционально его относительному удлинению)

Замечание.

Запишем закон Гука: F = - k Dl. Разделим левую и правую часть соотношения на произведение S l₀, тогда F/S l₀ = k Dl / S l₀ или F/S = (k l₀/ S) e, тогда s =(k l₀/ S) e, где (k l₀/ S) = Е.

 

Очевидно, что модуль Юнга определяется только свойствами образца. Его физический смысл заключается в следующем: модуль Юнга равен механическому напряжению, возникающему в образце при относительном его удлинении равным 1.

Сила трения – сила, препятствующая движению одного тела по поверхности другого, и составляющая часть от силы нормального давления.

F_трения = m N, где m - коэффициент трения, зависящий от степени обработки и от физических свойств соприкасающихся поверхностей, N – сила реакции опоры [ N = - P (III – ий закон Ньютона)].

Сила трения скольжения всегда направлена в сторону, противоположную скорости движения тела относительно поверхности, по которой оно движется. При небольших скоростях сила трения скольжения практически не зависит от скорости движения тела, при больших скоростях движения сила трения резко возрастает и она становится пропорциональной V ⁿ, где n = 2 или даже 3.

 

Различают трение покоя, трение скольжения и трение качения.

Трение покоя.

Если на тело действует сила F_тяги, как показано на рис.2, но тело сохраняет состояние покоя (неподвижно относительно поверхности, на которой нахо­дится), то это означает, что на тело одновременно действует сила, равная по величине и противоположная по направлению. Это и есть сила трения покоя.

 

 

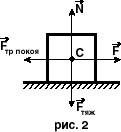
При уве­личении силы F_тяги, если тело сохраняет состояние покоя, увеличивается и сила трения покоя. Она всегда равна по величине и противоположна по направлению внешней действующей силе: F _{тр покоя} = - F_тяги. Поэтому на графике зависимости F _{тр покоя} от силы тяги F_тяги (см. рис. 3) угол наклона графика a составляет 45⁰

Сила трения покоя изменяется по величине от О до максимального зна­чения F_{тр покоя макс}, при которой начинается движение тела и, следовательно, оно равно при этом силе трения скольжения F_тр (F_тр = m N). Таким образом, сила трения покоя изменяется в следующих пределах: 0 < F _{тр покоя} < m N.

 

 

Сила трения скольжения……………

Сила трения качения мала по сравнению с силой трения скольжения. Она определяется по той же формуле, что и сила трения скольжения, но для этого случая m гораздо меньше. При больших скоростях сопротивление перекатыванию резко увеличивается и тогда следует рассматривать силу трения скольжения.

Приступая к решению задачи по динамике, прежде всего необходимо сделать чертеж, расставить все действующие на тело (тела) силы, выбрать систему отсчета. Затем записываем основной закон динамики для каждого тела в отдельности в векторном виде (SF = m a). После этого проектируем полученные векторные уравнения на оси координат, записываем уравнения связи (выражение для силы трения, соотношения кинематических величин и т.д.) и составляем из полученных алгебраических уравнения систему, в которой число уравнений должно быть равно числу неизвестных. Далее решаем полученную систему уравнений, получаем выражение для неизвестных физических величин, делаем проверку на размерность и, наконец, получаем численный ответ. В ответе (если речь идет о векторной величине) надо указывать не только численное значение (модуль величины), но и ее направление и точку приложения.

 

Замечание.

Принципиального отличия при решении задач на поступательное движение и движение тела по окружности (дуге окружности) нет. Различие только в формуле ускорения: в случае движения по окружности ускорение – центростремительное и оно равно: a = V² / R, где V – линейная скорость тела, R – радиус окружности, по которой двигается тело.

 

Примеры решения задач.

1. Два тела массами m₁ и m₂, связанные невесомой и нерастяжимой нитью, движутся вверх под действием силы F, приложенной к первому телу. Определить силу натяжения нити T.

Дано: m ₁; m₂; F; T -?

Решение.

Сделаем рисунок, соответствующий условию задачи.

Запишем основное уравнение динамики: å F = m а

Для первого тела: F + m₁ g + T₁ = m₁ a₁

Для второго тела: m₂ g + T₂ = m₂ a₂

Спроектируем полученные уравнения на оси координат:

на ось у: F - m₁g - T₁ = m₁a₁

m₂g + T₂ = m₂a₂

Т.к. по условию грузы связаны невесомой и нерастяжимой нитью, то: Т₁ = Т₂ = Т и а₁ = а₂ = а, тогда: F - m₁g - T = m₁a

Т - m₂g = m₂a

Решив систему полученных уравнений относительно Т, получим: Т= Fm₂/(m₁ + m₂).

Сделаем проверку на размерность:

Ответ: Т = F m₂ / (m₁ + m₂).

2. Через неподвижный блок перекинута нить, к которой подвешены два груза массами 2,5 кг и 1,5 кг соответственно. Определите ускорение грузов и силу натяжения нити. Трением в блоке пренебречь.

 

 

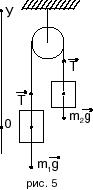
Дано: m ₁ = 2,5 кг; m₂ = 1,5 кг. а -? T -?

Решение.

Запишем основное уравнение динамики: å F = m а

Для первого тела: m₁ g + T₁ = m₁ a₁

Для второго тела: m₂ g + T₂ = m₂ a₂

Спроектируем полученные уравнения на оси координат:

на ось у: - m₁ g + T₁ = m₁a₁

- m₂g + T₂ = m₂a₂

Т.к. по условию грузы связаны невесомой и нерастяжимой нитью, то: Т₁ = Т₂ = Т и а₁ = а₂ = а, тогда: - m₁g + T = m₁a

- m₂g + Т = m₂a

Решим полученную систему уравнений относительно а: а = g (m₁ - m₂)/ (m₁ + m₂)

Затем из второг уравнения системы уравнений выразим Т, учтя полученный результат для ускорения: Т = m₂ (g + a)

Слелаем проверку на размерность: ;

Проведя расчеты, получим: а = 2,5 м/с², Т = 18,75 Н.

 

3. С какой силой давит человек массой 90 кг на пол лифта, движущегося с ус­корением 1,2 м/с² вверх? Принять g °= 9,8 м/с².

 

Дано: m = 90 кг; a = 1,2 м/с²; Р -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила тяжести mg и сила реакции опоры N, равная по III-му закону Ньютона весу тела Р, т.е. силе давления человека на пол лифта.

 

 

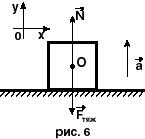
Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma или N + mg = ma

Спроектируем полученное векторное уравнение по осям координат:

Ось у: N - mg = ma, откуда N = m (g + a), следовательно P = m (g + a)

Проверка на размерность: [ P ] = кг м/с² = Н

Сделаем расчет: Р = 90 (9,8 + 1,2) = 990 Н.

 

4. С какой силой надо придавить тело массой 4,5 кг к вертикальной стене, чтобы оно двигалось вниз с ускорением 2 м/с²? Коэффициент трения груза о стенку равен 0,5.

 

Дано: m = 4,5 кг; a = 2 м/с²; m = 0,5. F -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила тяжести mg, сила, прижимающая тело к вертикальной плоскости F, сила трения F_тр и сила реакции опоры N.

 

 

Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma или N + mg + F + F_тр = ma

Спроектируем полученное векторное уравнение по осям координат:

Ось х: N - F = 0, т.к. по оси х движения нет, т.е. a_х = 0.

Ось у: F_тр - mg = - ma_у, где a_у = a, т.е. F_тр - mg = - ma_.

Запишем уравнение связи: F_тр = m N (по определению).

Решая совместно полученные три уравнения получаем: m F - mg = - ma,

откуда F = m(g - a)/ m.

Проверка на размерность: [ F ] = кг м/с² = Н

Сделаем расчет: F = 4,5 (10 - 2)/0,5 = 72 Н.

 

5. На наклонной плоскости длиной 13 м и высотой 5 м лежит груз массой 26 кг. Коэффициент трения равен 0,5. Какую минимальную силу надо приложить к грузу вдоль плоскости, чтобы сдвинуть его вниз?

 

Дано: l = 13 м; h = 5 м; m = 26 кг; m. = 0,5; a = 0. F -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила, стаскивающая тело с наклонной плоскости сила F, сила реакции опоры N, сила трения F_тр и сила тяжести mg.

 

 

Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma или F + N + F_тр + mg = ma

Спроектируем полученное векторное уравнение по осям координат:

Ось х: F + mg_х - F_тр = 0, т.к. a = 0 (по условию), где mg_х - проекция силы тяжести mg на ось х.

Ось у: N - mg_у = 0, т.к. a = 0 (по условию), где - проекция силы тяжести mg на ось у.

Запишем уравнение связи: F_тр = m N (по определению).

mg_х = , mg_у = (из геометрических соображений)

Решая совместно полученные уравнения получаем:

F + - = 0, откуда F = mg

Проверка на размерность: [ F ] = = Н

Сделаем расчет: F = = 20 Н.

6. Шайба, лежащая на вращающемся диске на расстоянии 15 см от центра диска, соскальзывает с него. когда число оборотов достигает значения 1 об/с. Найти коэффициент трения между шайбой и поверхностью диска.

 

Дано: R = 15 см = 0,15 м; n = 1 об/с.m -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила тяжести mg, сила трения F_{тр покоя} и сила реакции опоры N.

 

 

Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma

или mg + F_{тр покоя} + N = ma_цс

Спроектируем полученное векторное уравнение по осям координат:

Ось х: F_{тр покоя} = ma_цс.

Ось у: N - mg = 0, т.к. т.к. по оси у движения нет, т.е. a_у = 0..

В данном случае центростремительное ускорение телу сообщает сида трения покоя, которая, как известно, может принимать любое значение от нуля до максимальной силы трения покоя. По мере роста скорости вращения диска сила трения покоя увеличивается до своего максимального значения. При дальнейшем возрастании скорости нет достаточных «заворачивающих» смл, и тело почти по касательной движется на периферию диска.

В связи с этим можем записать уравнение связи:

F_{тр покоя макс} = m N (по определению).

Решая совместно полученные уравнения получаем:

m mg = ma_цс, откуда имеем a_цс = m g, но a_цс = w²R (по определению),

тогда m g = w²R, где w = 2pn (по определению),

и, наконец, m g = 4 p² n² R, откуда m = 4 p² n² R/ g

Проверка на размерность: [ m ] = = 1

Сделаем расчет: m = = 0,6.

7. Определить радиус R горбатого мостика, имеющего вид дуги окружности, при условии, что давление автомобиля, движущегося со скоростью V = 90 км/час, в верхней точке мостика уменьшилось вдвое.

 

Дано: V =90 км/ч = 25 м/с; P = 0,5 P₀; R -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила тяжести mg, и сила реакции опоры N. Следует учесть, что центростремительное ускорение a_цс направлено вертикально вниз.

 

 

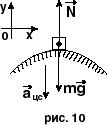
Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma или N + mg = ma_цс

Спроектируем полученное векторное уравнение по осям координат:

Ось у: N - mg = - ma_цс, где a_цс = V²/R (по определению), тогда N = mg - mV²/R.

По 3-му закону Ньютона N = - Р, следовательно N = 0,5 N₀, где N₀ = mg (исходя из условия).

Тогда имеем: 0,5 mg = mg - mV²/ R, откуда R = V² /0,5 g

Проверка на размерность: [ R ] = = м

Сделаем расчет: R = = 125 м.

8. Самолет при скорости 360 км/час делает в вертикальной плоскости петлю Нестерова радиусом 500 м. Насколько отличается веа летчика в нижней и верхней точках петли, если его масса равна 80 кг.

 

Дано: V =360 км/ч = 100 м/с; R = 500 м; m = 80 кг; DР -?

Решение.

Сделаем чертеж и расставим все силы, действующие на тело: сила тяжести mg, и сила реакции опоры N. Следует учесть, что центростремительное ускорение a_цс в нижней точке петли направлено вертикально вверх, а в верхней точке - вертикально вниз.

 

 

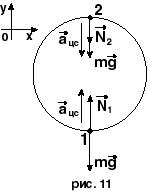
Выберем систему отсчета, связанную с Землей.

Запишем основной закон динамики: SF = ma

Тогда для нижней точки петли 1 имеем N₁ + mg = ma_{цс 1}

Аналогично для верхней точки 2: N₂ + mg = ma_{цс 2}

Спроектируем полученные векторные уравнения по осям координат:

Ось у: для нижней точки 1 имеем

- N₁ + mg = - ma_{цс 1}, откуда N₁ = ma_{цс 1} + mg.

для верхней точки 2:

N₂ + mg = ma_{цс 2}, откуда N₂ = ma_{цс 2} – mg.

 

По 3-му закону Ньютону N = - P, следовательно P = N и DP = DN.

Учтя, что модули центростремительного ускорения в нижней и верхней точках петли равны, т.к. самолет двигается по окружности с постоянной скоростью, запишем: Р₁ = ma_{цс 1} + mg.

Р₂ = ma_{цс 2} - mg.

Поскольку DР = Р₁ - Р₂, тогда DР = ma_цс + mg - ma_цс + mg = 2 mg

 

Задачи для самостоятельного решения