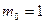Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой
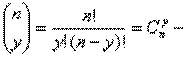
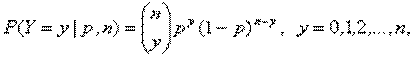
где
число сочетаний из n элементов по y, известное из комбинаторики.
Для всех y, кроме 0, 1, 2, …, n, имеем
P(Y=y)= 0.
Функция распределения имеет вид:
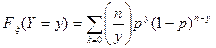
Параметры:
1.Математическое ожидание
M(y) = np
2.Дисперсия
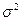 = np (1-p)= npq
= np (1-p)= npq
3.Характеристическая функция
f  (t)=
(t)= 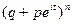
4.Начальный момент r-го порядка
 =
=  =
= 
5.Абсолютный момент r-го порядка
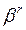 =
= 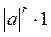 =
= 
6.Факториальный момент r-го порядка
f  =
= 
7.Центральный момент r-го порядка
 =(a-a)
=(a-a)  ∙1=0
∙1=0
8.Медиана
Одно из 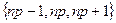
9.Мода
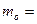 (n+1)p
(n+1)p
Распределение Паскаля.
Функция вероятности имеет вид:
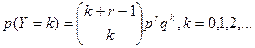
Функция распределения не выражается в элементарных функциях.
Параметры:
1. Математическое ожидание
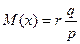
2. Дисперсия
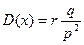
3. Характеристическая функция
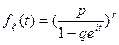
8. Медиана
нет
9. Мода
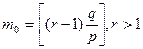
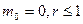
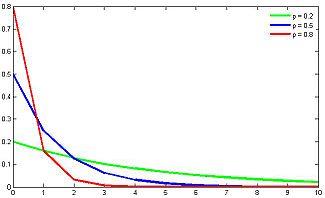
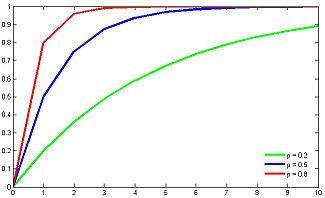
Геометрическое распределение.
Говорят, что случайная величина 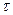 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром  , если
, если 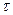 принимает значения k=1,2,3,… с вероятностями
принимает значения k=1,2,3,… с вероятностями 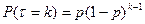 . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p. Таблица распределения
. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p. Таблица распределения 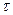 имеет вид
имеет вид
 или
или 
Функция распределения имеет вид:
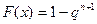
Параметры:
1.Математическое ожидание
M(x)= 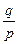
2.Дисперсия
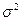 =
= 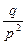
3.Характеристическая функция
f  (t)=
(t)= 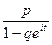
8.Медиана
нет
9.Мода
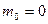
Гипергеометрическое распределение.
Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид:

Функция распределения не выражается в элементарных функциях.
Параметры:
1.Математическое ожидание
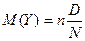
2.Дисперсия
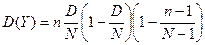
3.Характеристическое уравнение
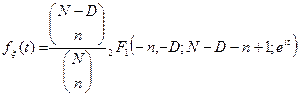
8.Медианы
нет
9.Мода
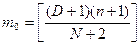
Распределение Пойе.
Плотность вероятности случайной величины имеет вид:
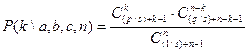
где 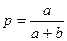 ,
, 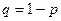 ,
, 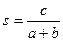
Параметры:
1.Математическое ожидание
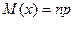
2.Дисперсия
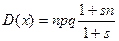
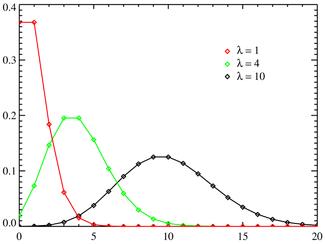
Распределение Пуассона.
Случайная величина 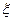 имеет распределение Пуассона, если
имеет распределение Пуассона, если 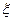 принимает значения k=0,1,2,… с вероятностями
принимает значения k=0,1,2,… с вероятностями
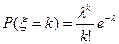 ,где λ>0 – параметр распределения Пуассона.
,где λ>0 – параметр распределения Пуассона.
Функция распределения имеет вид:
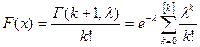
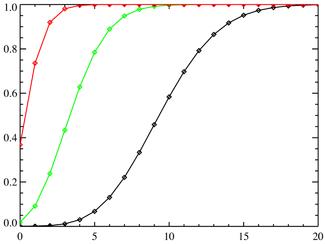
Параметры:
1.Математическое ожидание
M(x)= 
2.Дисперсия
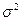 =
= 
3.Характеристическая функция
f  (t)=
(t)= 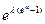
8.Медиана
нет
9.Мода
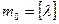
Логарифмическое распределение.
Функция вероятности имеет вид:
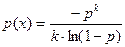
Функция распределения имеет вид:
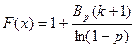 , где
, где  - неполная бета-функция
- неполная бета-функция
Параметры:
1.Математическое ожидание
M(x)= 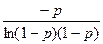
2.Дисперсия
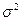 =
= 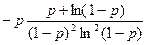
3.Характеристическая функция
f  (t)=
(t)= 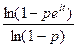
f  =M(x
=M(x 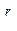 )=
)= 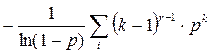

8.Медиана
нет
9.Мода