Вырожденное распределение.
Говорят, что случайная величина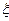 
имеет вырожденное распределение в точке a 
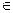R, если 
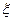принимает единственное значение a с вероятностью 1, т.е. P( 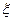=a)=1.
Данное распределение также называют причинным.
Функция распределения 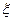имеет вид
F 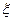(x) = P ( 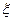<x) =P(a<x) =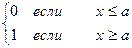 
Распределение Бернулли.
Распределение часто используется при контроле качества продукции.
Говорят, что случайная величина 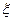имеет распределение Бернулли с параметром p, если 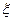принимает значения 1 и 0 с вероятностями p и 1-p=q соответственно. Случайная величина 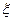с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p: ни одного успеха или один успех. Таблица распределения 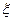имеет вид:
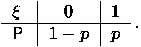
Биноминальное распределение.
Распределение часто используется при контроле качества продукции, когда объем партии (генеральной совокупности) многократно превышает объем контрольной выборки n.
Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой
где
число сочетаний из n элементов по y, известное из комбинаторики.
Для всех y, кроме 0, 1, 2, …, n, имеем P(Y=y)= 0.
Распределение Паскаля.
Распределение часто используется при контроле качества продукции.
Функция вероятности имеет вид:
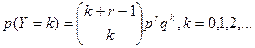
Геометрическое распределение.
Геометрическое распределение достаточно популярно, в частности, при разработке математических методов контроля качества промышленной продукции.
Говорят, что случайная величина 
имеет геометрическое распределение с параметром 
, если принимает значения k=1,2,3,… с вероятностями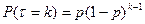 
. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p. Таблица распределения 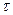имеет вид
или 
Гипергеометрическое распределение.
Широко используется при статистическом контроле качества продукции и выборочных обследованиях.
Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид:
Распределение Пойе.
Этот закон также находит важные применения при статистических исследованиях заболеваний - эпидемий.
Плотность вероятности случайной величины имеет вид:
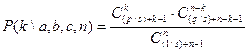
где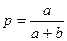 
, 
, 
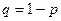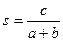
Распределение Пуассона.
Случайная величина 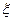имеет распределение Пуассона, если 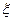принимает значения k=0,1,2,… с вероятностями
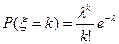,где λ>0 – параметр распределения Пуассона.
Логарифмическое распределение.
Функция вероятности имеет вид:
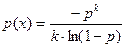
Распределение Бореля-Таннера.
Дискретное распределение вероятностей случайной величины ξ, принимающей значения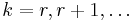 
с вероятностями
где r > 0 — целое и 0 < α < 1.
11. 
Равномерное распределение.
Непрерывная случайная величина 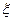, принимающая значения на отрезке [ a, b ], распределена равномерно на [ a, b ], если ее плотность распределения p 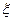(x)
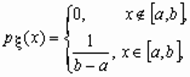
Распределение Симпсона.
Cлучайная величина ξ имеет треугольное распределение (распределение Симпсона) на отрезке [ a, b ] (a < b), если
