Схема приведена на рисунке 4.9. Элементы 
– элементы задержки, т.е. память компьютера (аналог линии задержки на время интервала дискретизации). Элементы 
это умножители на соответствующий коэффициент (весовые коэффициенты). По прошествии 
выборок на вход сумматора через каждый интервал дискретизации будет действовать выборок.
Формула (4.40) называется разностным уравнением фильтра.
Определим передаточную функцию фильтра, для начала определив изображение выходного сигнала
,(4.41)
или по-иному
. (4.42)
Теперь легко найти передаточную функцию
,(4.43)
. (4.44)
Можно также найти комплексный коэффициент передачи фильтра, заменив в формуле (4.44)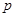 
на 
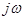
, (4.45)
а также системную функцию
. (4.46)
Анализируя ККП фильтра, можно сказать, что частотные характеристики фильтра будут периодическими с частотой равной 
и периодом, равным периоду дискретизации.
Импульсная характеристика трансверсального фильтра
Импульсная характеристика трансверсального фильтра (рисунок 4.10) будет конечной и содержать импульс. Это следует из структурной схемы фильтра. Величины импульсов равны коэффициентам 
Это есть КИХ – фильтр (с Конечной Импульсной Характеристикой). Формула (4.45) по своему виду является прямым преобразованием Фурье от 
(отсчет импульсной характеристики).
4.5. 
Трансверсальный фильтр первого порядка
Порядок фильтра определяется количеством элементов задержки, использованных в нем. Схема трансверсального фильтра первого порядка представлена на рисунке 4.11. Выходной сигнал этого фильтра можно записать с учетом выражения (4.40)
(4.47)
Запишем ККП данного фильтра по (4.45)
, (4.48)
а теперь, используя формулы Эйлера немного преобразуем (4.48), выделив действительную и мнимую части
. (4.49)
Найдем АЧХ фильтра
(4.50)
Теперь рассмотрим, как изменяется АЧХ фильтра при изменении весовых коэффициентов .
а) Пусть 
, тогда ККП такого фильтра равен (4.50)
. (4.51)
Построим АЧХ данного фильтра
Если сигнал таков, что он удовлетворяет теореме Котельникова, т.е. спектр его лежит в диапазоне от 0 до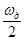 
, то для такого сигнала фильтр будет представлять собой ФНЧ. Если ширина спектра сигнала больше, чем 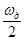, то такой фильтр является для данного сигнала гребенчатым. Он выделяет частоты близкие к 
и полностью подавляет частоты 
и т.д.
b) Поменяем коэффициенты 
. Получим фильтр со следующим ККП
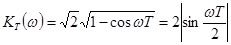. (4.52)
Построим АЧХ
Для сигналов, удовлетворяющих теореме Котельникова этот фильтр будет представлять собой ФВЧ. Когда ширина спектра больше, это будет гребенчатый фильтр, который будет выделять частоты и подавлять
