Основы теории дискретных сигналов
Последние годы характеризуются быстрым развитием дискретных систем управления и систем передачи информации, в которых широко применяются математическое моделирование процессов фильтрации, основанное на использовании ЭВМ. Это направление оказывает большое влияние на развитие теории и техники цепей и сигналов.
Цифровые фильтры имеют ряд преимуществ. Основные из них: стабильность характеристик, недостижимая в аналоговых фильтрах – обусловлена преобразованием континуального сигнала в двоичное число, представленное стандартными сигналами (импульсами и паузами).
Дискретизация аналоговых сигналов
Аналоговым называется сигнал непрерывный во времени и по уровню.
Дискретным называют сигнал непрерывный по уровню и отличный от нуля в дискретные моменты времени.
Интервал дискретизации 
выбирается, исходя из теоремы Котельникова
, (4.1)
где 
- максимальная частота в спектре сигнала 
.
В дальнейшем будем использовать следующее соотношение
. (4.2)
Дискретный сигнал можно представить в виде произведения аналогового сигнала и дискретизирующей 
– функции
. (4.3)
Значения функции переходят в весовые коэффициенты – функций.
В дальнейшем будем предполагать
а) Сигнал существует только при 
. При 
.
b) Сигнал конечен во времени. 
– длительность сигнала, тогда количество выборок будет конечно и равно 
, а значит
, (4.4)
следовательно формулу (4.3) можно записать так
. (4.5)
Спектральная плотность дискретного сигнала
Дискретный сигнал – непериодический, а значит обладает сплошным спектром. Определим спектральную плотность, используя для этого прямое преобразование Фурье.
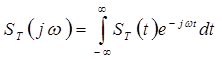, (4.6)
а т.к. сигнал задан только для неотрицательного времени, то
. (4.7)
И в конечном итоге, используя основное свойство – функции
. (4.8)
Формулой (4.8) подтверждается известное свойство спектра дискретного сигнала – его периодичность. Если рассматривать спектральную плотность на кратных частотах
, (4.9)
то спектральная плотность будет величиной неизменной.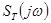 
– периодическая функция частоты с периодом равным периоду дискретизации.
Еще одной особенностью спектральной плотности дискретного сигнала является то, что она выражается в виде обычной суммы конечного числа слагаемых, равных .
Дискретное преобразование Фурье
При проведении спектрального анализа с использованием ЭВМ количество отсчетов спектральной плотности анализируемого сигнала должно быть ограничено, т.к. объем памяти ЭВМ ограничен, поэтому необходимо осуществить дискретизацию спектральной плотности. Пусть эта дискретизация осуществляется с шагом дискретизации по частоте 
. На рисунке 4.2 даны временные и частотные диаграммы процесса дискретизации.
После дискретизации аналогового сигнала спектр его становится периодическим (рисунок 4.2 b)), а дискретной спектральной плотности соответствует периодический дискретный сигнал (рисунок 4.2 c)).
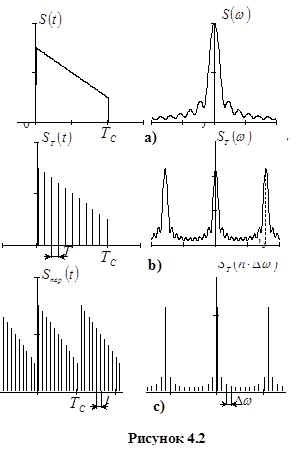
Период нового сигнала определим следующим способом:
. (4.10)
Определим интервал дискретизации частоты
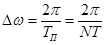. (4.11)
Минимальное количество отсчетов спектральной плотности на одном периоде равно
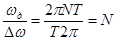, (4.12)
т.е. количество выборок в частотной области равно количеству выборок во временной области.
Подставим (4.11) в (4.8), получим
, (4.13)
, 
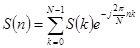, (4.14)
где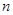 
– номер отсчета спектральной плотности
Две последние формулы и есть аналитические выражения дискретного преобразования Фурье.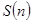 
иногда называют коэффициентами дискретного преобразования Фурье.
Формула (4.14) есть прямое дискретное преобразование Фурье. Есть также обратное преобразование Фурье
, 
. (4.15)
Недостатком дискретного преобразования Фурье является то, что при достаточно большом необходимо производить очень много операций умножения, а это занимает большой промежуток времени. А значит при большом количестве выборок невозможно провести обработку информации в реальном масштабе времени. Поэтому были разработаны алгоритмы быстрого преобразования Фурье.
