Величины крутящих моментов, Н·м

L
Материал	Сталь 15	Сталь 20	Сталь 35	Сталь 40	Сталь 45
Вариант
		%
								2.30

 

Посадки с натягом относятся к неподвижным соединениям. Возможны три вида нагрузок, передаваемых неподвижным сопряжением:

1) крутящий момент (М_кр);

2) осевая сила (Р_ос);

3) крутящий момент и осевая сила (М_кр и Р_ос).

Давление, необходимое для передачи данных нагрузок, определяют в зависимости от ее вида:

; ; .

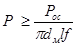Рассчитав давление (Р), необходимое для передачи заданной нагрузки, на основании зависимостей, известных из решения задачи Лямэ для толстостенных цилиндров, можно определить N_min (м), способный передать указанные ранее нагрузки

,

где Е_D и E_d – модули упругости, Па;

C_D и С_d – коэффициенты, определяемые по формулам

; ;

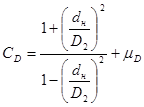d₁ и D₂ – из рис. 7; µ_D – отв. и µ_d – вал – коэффициенты Пуассона; сталь – 0,3; чугун – 0,25; бронза – 0,35; латунь – 0,38.

При запрессовке срезаются неровности отверстия и вала на 60 % от их высоты. Тогда расчетный натяг для выбора неподвижной посадки можно найти по формуле

N_расч = N_min + 1.2(R_zD + Rzd).

 

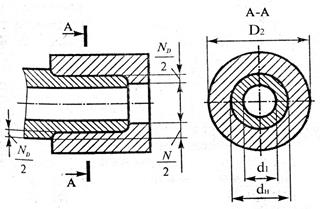
Рис. 8. Схема к расчету посадок с натягом

 

При выборе стандартной посадки необходимо выдержать следующие условия относительно неподвижности сопрягаемых деталей:

N_{min ст} ≥ N_расч.

Чтобы проверить детали на прочность, надо вычислить напряжения, Па, которые возникают в них при натяге, наибольшем для выбранной посадки:

.

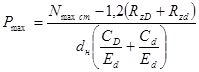Эти напряжения для охватывающей и охватываемой детали будут соответственно равны:

; .

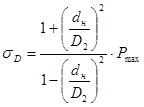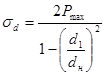Если эти напряжения меньше предела текучести материала, т.е.

σ_D < σ_TD и σ_d<σ_Td,

значит, посадка выбрана правильно.

(Однако перед массовым применением этих посадок надо выполнить экспериментальную проверку).

 

Пример. Подобрать стандартную посадку с натягом для следующих условий:

Ø = d_н = 0,15 м;

D₂ = 0,25 м;

l = 0,18 м;

М_{к р} = 9000 Н·м;

d ₁ = 0 (вал сплошной);

втулка и вал – сталь 40;

ƒ = 0,085;

R_zd = 6,3 мкм; R_zD = 10 мкм.

 

1. Определить значение необходимого давления:

.

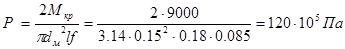2. Находим N_min:

где

;

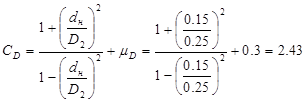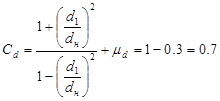(т.к. d₁ = 0).

3. Определяем расчетный натяг:

N_расч = N_min + 1,2 (R_zD + R_zd) = 27 + 1,2(10 + 6.3) = 46,5 мкм.

4. По таблицам находим, что по условию N_{min ст} ≥ N_расч удовлетворяет только одна предпочтительная посадка с N_min = 60 мкм:

Ø150 .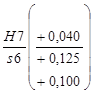

 

5. Находим Р_max, которое может возникнуть после запрессовки при использовании посадки Ø150 Н7/s6:

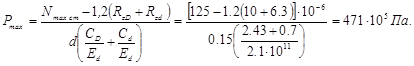
6. Наибольшее напряжение во втулке:

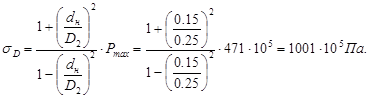
7. Условие прочности охватывающей детали выдерживается, т.к. для стали 40 σ_т = 3400 Па и σ_D < σ_TD, что соответствует правильно выбранной посадке.

Если бы условие прочности не было выдержано для этой посадки, то следовало проверить рекомендуемые посадки и выбрать ту из них, которая удовлетворяет обоим условиям.

Результаты расчета сводим в табл. 6.

 

Таблица 6

Параметры размера	Отверстие	Вал
Допуск, мкм	ТД = 40
Основное отклонение, мкм	EJ = 0
Верхнее отклонение, мкм	ES = 40
Нижнее отклонение, мкм	EJ = 0

 

Предельные размеры вала и отверстия:

D_max = D + ES = 150 + 0,040 = 150,040 мкм;

D_min = D + EJ = 150 + 0 = 150 мкм;

d_max = d + es = 150 + 0,125 = 150,125 мкм;

d_min = d + ei = 150 + 0,100 = 150,100 мкм.

 

Допуски размеров вала и отверстия:

TD = ES – EJ = 40 – 0 = 40 мкм;

TD = D _max – D _min = 150,040 – 150 = 0,040 мм;

Td = es – ei = 125 – 100 = 25 мкм;

Td = d _max – d _min = 150,125 – 150,100 = 0,025 мм.

 

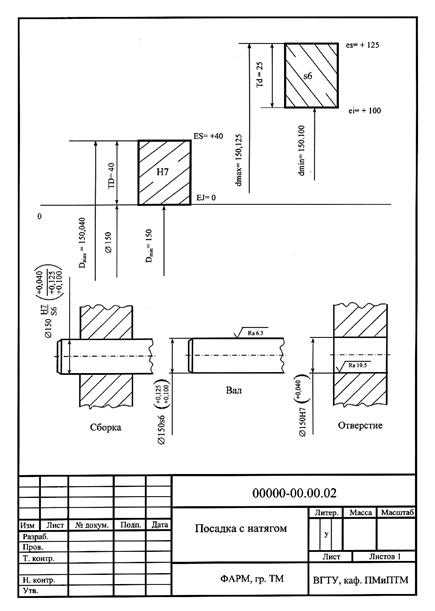
Рис. 9. Поля допусков и посадок в гладком цилиндрическом

соединении с натягом

Величины предельных натягов:

N_max = d _max – D_min = 150,125 – 150 = 0,125 мм;

N_max = es – EJ = 125 – 0 = 125 мкм;

N_min = d_min – D_max = 150,10 – 150,040 = 0,060 мм;

N_min= ei – ES = 100 – 40 = 60 мкм.

 

Допуск посадки:

TS = N_max – N_min = 125 – 60 = 65 мм;

TS = TD + Td = 40 + 25 = 65 мм.

 

Характеристика посадки:

посадка Æ 150 выполнена в системе «отверстие» с натягом, комбинированная по квалитетам (отверстие Н 7, вал s 6).

 

Переходные посадки

Переходные посадки применяют при центрировании деталей. Передача нагрузки соединением обеспечивается дополнительным креплением: шпонками, штифтами и другими крепежными средствами.

Точность центрирования и легкость сборки и разборки соединения при применении небольших усилий возможна лишь при небольших колебаниях допустимых натягов и зазоров, поэтому переходные посадки предусмотрены только в относительно точных квалитетах: валов в 4 – 7- м, отверстиях 5 – 7- м. Отверстия в переходных посадках, как правило, применяют на один квалитет грубее вала.

Характер переходных посадок определяется вероятностью получения при сборке натягов или зазоров в сопряжении.

 

 

Таблица 7

Варианты заданий к переходным посадкам

Посадка	H7/k6	H7/m6	M7/h6	K7/h6	N7/h6
Вариант

 

Рассчитать переходную посадку – это значит определить вероятность получения натягов (зазоров) при заданных условиях. В основу расчета положен ряд допущений: рассеяние действительных размеров деталей подчиняется закону нормального распределения (закону Гаусса) (рис. 10); Теоретическое рассеяние 6 s равно допуску детали, а центр рассеяния совпадает с серединой поля допуска. Распределение натягов или зазоров в этом случае также будет подчиняться нормальному закону, а вероятности их получения определяются с помощью интегральной функции вероятности Ф (z).

 

Пример расчета

Дано: переходная посадка .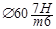

Необходимо: определить вероятность натяга и зазора в данном соединении.

По таблице ГОСТ 25346 – 82 находим:

Д – отв.: ES = + 30 мкм; EJ = 0; TD = 30 мкм.

d – вал: es = + 30 мкм; ei = + 10 мкм; Td = 20 мкм.

В данном сопряжении возникают как зазоры, так и натяги:

S_max = ES – ei = 30 = 10 = 20 мкм;

N_max = es – EJ = 30 – 0 = 30 мкм.

Допуск посадки:

ТП = ТД + Тd =30 + 20 = 50 мкм.

Полагаем, что рассеивание размеров отверстия и вала подчиняется нормальному закону.

Примем практический диапазон рассеивания равный 6 σ, т.е. допуск деталей Т = 6 σ, где σ – среднее квадратичное отклонение размеров вала и отверстия.

Определяем:

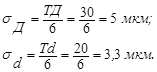
Из теории вероятностей известно, что если две или несколько случайных величин рассеиваются по нормальному закону, то суммарное распределение этих же величин будет подчиняться тому же закону.

Среднее квадратичное отклонение суммарной совокупности определяется по формуле:

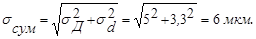
Выразим средние значения размеров отверстия и вала:

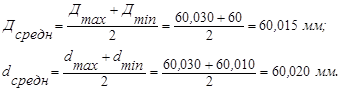
В этом случае мы получаем натяг:

Д_средн – d_средн = 60,015 – 60,020 = - 0,005 мм = - 5 мкм.

Вычислим вероятность значения натяга в пределах от 0 до 5 мкм, т.е. найдем площадь, ограниченную линией симметрии кривой и ординатой, расположенной на расстоянии 5 мкм от линии симметрии (у).

Эта площадь определяется интегралом:

.

В нашем случае х = 5 мкм, следовательно, .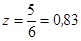

По таблицам значения функции Ф (z), которые приводятся в различных справочниках и учебных пособиях, находим, что при z = 0,83 вероятность натяга в пределах от 0 до 5 мкм составляет 0,2967.

Вероятность получения натягов в соединении:

Р_N = 0,5 + 0,2967 = 0,7967 или 79,67 %.

Вероятность получения зазоров (не заштрихованная площадь под кривой распределения):

Р_S = 1 – 0,7967 = 0,2033 или 20,33 %.

Вероятный натяг – 5 – 3 σ = - 5 – 3 · 6 = - 23 мкм и зазор – 5 + 3 σ = -5 + 3 · 6 = +13 мкм будут практически предельными натягом и зазором. Однако этот расчет является приближенным, т.к. в нем не учтены возможности смещения центра группирования относительно середины поля допуска вследствие систематических погрешностей.

Строим схемы полей допусков соединяемых деталей, эскизы соединения и отдельных его деталей и показываем результат расчета вероятности зазора и натяга (рис. 10).

Контрольные вопросы

1. В каких квалитетах предусмотрены переходные посадки и почему?

2. Перечислите области техники, в которых предпочтительно предусматривать переходные посадки.

3. Выполните анализ посадок H/n; H/m; H/k и H/j_s для квалитета и номинального размера вашего задания. Что для них характерно?

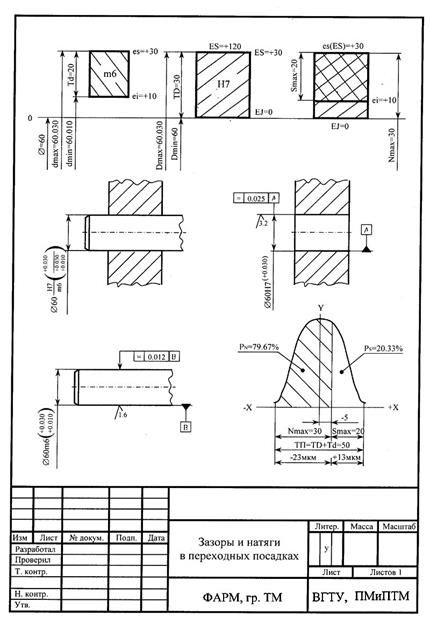
Рис. 10. Схема полей допусков, зазоры и натяги в переходных посадках, эскизы сопряжения и его деталей